闫氏DP 学习笔记 一

说在前面

本博客中“闫氏DP”指的是2011年NOI金牌保送北京大学计算机系的算法选手闫学灿（yxc/y总）在教授动态规划时提出的“从集合角度分析DP问题的思维方式”。并非指代某类动态规划题型、也不是某种求解动态规划的固定算法。该文章仅作“闫氏DP”的学习笔记，一并附上例题的个人理解。为了使文章生动有趣，后文使用“yxc”或“y总”指代闫学灿本人。

代码均经过本人实际测试AC后才给出（故意演示超时的朴素做法也会选择性展出），代码总耗时也会给出，以AC记录的时间为准。代码均由CLion格式化，方便阅读。

了解动态规划

了解DP的大佬可以直接看到下一节~

动态规划（Dynamic Programming，简称DP）是运筹学的一个分支，用于求解多决策过程的最优解，最初由Bellman等人提出。当一个过程存在多个决策，且每个决策之间都会互相影响（最终影响到结果）时，就可以考虑使用动态规划。动态规划建立在递推关系之上，主张用已有的状态去表示未知的状态。正因如此，找出各个决策所产生的状态之间的关系是至关重要的（这个重要信息后期会被转译为状态转移方程求解DP）。

常见的动态规划根据问题的特点，分别被称作：线性DP，背包，树上DP，区间DP，数位DP，插头DP……

传统DP分析法

DP自诞生之初就用来解决多决策过程问题，解决多决策问题就需要考虑如下性质，这些也是传统动态规划所考虑的角度：

1. 状态：相当于 dp[i][j]所表示的意义，各个状态之间有内在的联系
2. 无后效性：第 个状态仅由第 个状态决定，而不是其他的任何状态
3. 最优子结构：把最优解拆开成一个个小部分，每个组成最优解的部分也一定是最优的

这样的传统方法看起来比较抽象，但这种方法的确是DP问题的标准解法，因为上述几种性质组成一个完整的动态规划问题。自然针对其组成部分提出的解决方案是最为标准的。

闫氏DP分析法

这张图（讲课板书）很清晰的阐明了闫氏DP分析法的内核，其中动态规划问题的求解依赖于状态的表示和计算，而搞清楚状态表示又需要读题分析需要规划的总集合、以及问题的属性。这个基本框架在求解DP问题中发挥了极其重要的作用。

状态计算里有一个非常重要的地方——搞清楚“前驱状态的转移”。就是需要解释清楚当前的状态是怎么由前面一个状态得到的。虽然说起来用不了几个字，但是这也是DP问题的难点，毕竟转移方程是DP问题的灵魂，得到了方程整个问题也就解决了。

线性DP

迷宫型 线性DP

P1216 数字三角形

题目传送门

难度：普及-

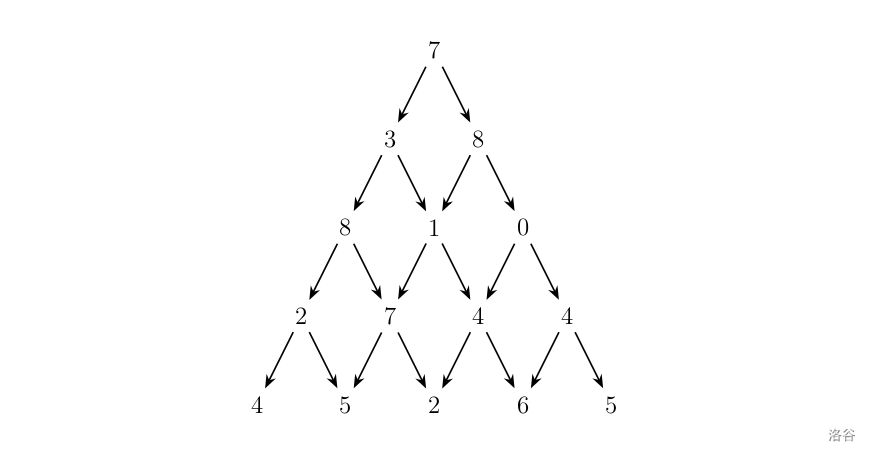
观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

在上面的样例中，从 的路径产生了最大权值。

这个题似乎连读入都要好好想一想

定义一个二维 map数组，map[i][j]表示第 层从左数第 个数，所以实际读入的数组输出出来会与上图有一些差别，为了与读入保持一致，使用下面给出的数组进行思考：

1
2
3
4
5

7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

我们需要解决的问题的总集合就是从第一层走到第五层的可能路径，而属性就是 max（最大值）。这些都是读题能找出来的东西。

接着思考状态表示：摸清楚前驱状态。如果按照正向思维，从上往下遍历（第一次在第一层、第二次在第二层），会有一个问题——不知道前驱状态。那我们就反着来，由最下层向最上层遍历！

既然向上遍历，我们就脑补一下——把题图里面所有的箭头反向。这样一来上层的总和就可以用下边的点之和来转移了。例如倒数第二层的 ，表示出来就是 dp[4][2]；它可以用下层的 或 得来，分别对应 dp[5][2]和 dp[5][3]。推广一下就是 dp[i][j]可以由 dp[i + 1][j]和 dp[i + 1][j + 1]得来，结合先前所述的状态表示，得出状态转移方程：dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + map[i][j]。那么这个最大和从下边一路推到最上边，到达点 （顶点）时显然就是整个问题的解，因此最后输出 dp[1][1]即可。

最后是初始化：明显地，dp数组的最后一层应该全部赋值为 map数组的最后一层，这样才能让整个算法基于金字塔的最底端进行递推，得到正确答案（或者可以直接用 map数组计算）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#include <bits/stdc++.h>
#define N 1010
using namespace std;

int dp[N][N], mp[N][N];
int main() {
	int r;
	cin >> r;
	for (int i = 1; i <= r; i ++) {
		for (int j = 1; j <= i; j ++) {
			cin >> mp[i][j];
		}
	}
	for (int i = 1; i <= r; i ++) dp[r][i] = mp[r][i]; // 初始化最后一层
	for (int i = r - 1; i >= 1; i --) { 
                // 反着扫每一层
		for (int j = 1; j <= r - 1; j ++) {
                        // 每一列
			dp[i][j] = max(dp[i + 1][j], dp[i + 1][j + 1]) + mp[i][j];
		}
	}
	cout << dp[1][1] << endl;
	return 0;
}

由于命名冲突，原文中 map数组实为 mp数组。

总用时： 记录

AcWing1015 摘花生

原题地址：AcWing1015（原AcWing1017）

难度：简单

不知道为什么听课的时候y总说是1017现在变成1015了（但网址还是1017）……可能是题库变动，前面少了两道题吧……

Hello Kitty想摘点花生送给她喜欢的米老鼠。

她来到一片有 行 列的网格状道路的矩形花生地(如下图)，从西北角进去，东南角出来。

地里每个道路的交叉点上都有种着一株花生苗，上面有若干颗花生，经过一株花生苗就能摘走该它上面所有的花生。

Hello Kitty只能向东或向南走，不能向西或向北走。

问Hello Kitty最多能够摘到多少颗花生。

这道题属于经典的“走方格最值型线性DP”（自己瞎起的名字），很多DP题目里都有它的影子。例如洛谷 P1176 路径计数2、洛谷 P1958 上学路线和AcWing 1018 最低通行费。

首先读入整个地图，用数组w存储每个点的花生数（点权）。

接下来解题：状态表示，读题——总集合是从点 （左上角）走到点 （右下角）的所有路径，属性则是max。

接下来是状态计算，既然全集是所有合法路径，那我们如何划分这个“合法路径集”呢？

再读题，它说：“只能向东或向南走”。对应到方向标（上北下南左西右东），那就是只能向右或向下走（不走回头路）一直到右下角。假如她某次移动到了点 （ ），那么她可能是从点 或者是 过来的。既然如此，将两条支路的数据汇集起来，取一个最大值max，不就是整道题的答案吗？因而，状态转移方程就是dp[i][j] = max(dp[i - 1][j] + w[i][j], dp[i][j - 1] + w[i][j])，等价于dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + w[i][j]。由于递推是正向的，到点 结束，因此最终输出dp[r][c]。

当我们高高兴兴写代码的时候就会发现一些问题：如果我在第一列（最左边那一列），按照转移方程，左侧的点将会汇入计算，但第一列左侧的点并不存在；同理，第一行（最上边那一行）的上侧的点也不存在。那么该怎么样处理这样的特殊情况呢？

一般来说，OIer在开数组存值时，会从下标 开始——但是在计算机中，一个数组真正的下标从 开始。因此可以考虑在第一列和第一行的左侧和上侧点在w数组中设为-INF（ 和负数均可），总之让它们成为“虚点”，对整体结果无实际影响就行。或者在循环中写入特判第一列和第一行的情况，两种方案均可。我选择了比较方便的填充特殊值法，代码在下边给出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

// 给地图外部的行/列赋特殊值

#include <bits/stdc++.h>

#define INF 0x3f3f3f3f
#define N 110
using namespace std;

int dp[N][N], w[N][N];

int main() {
    int T, r, c;
    cin >> T;
    while (T--) {
        cin >> r >> c;
        for (int i = 1; i <= r; i++) {
            for (int j = 1; j <= c; j++) {
                cin >> w[i][j];
            }
        }
        // 初始化特殊行/列
        for (int i = 0; i <= r; i++) w[0][i] = -INF;
        for (int i = 0; i <= c; i++) w[i][0] = -INF;
        for (int i = 1; i <= r; i++) {
            for (int j = 1; j <= c; j++) {
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + w[i][j];
            }
        }
        cout << dp[r][c] << endl;
    }
    return 0;
}

当然，这道题也可以不填充特殊值，因为全局定义的数组在内存中的默认值就是0，但为了保险这里还是加上了负无穷的填充。

总用时： 记录

P1004 方格取数

题目传送门

难度：普及+/提高

来源：NOIp 提高组  2000

2008年NOIP官方送来的双倍经验，请注意查收：P1006 传纸条

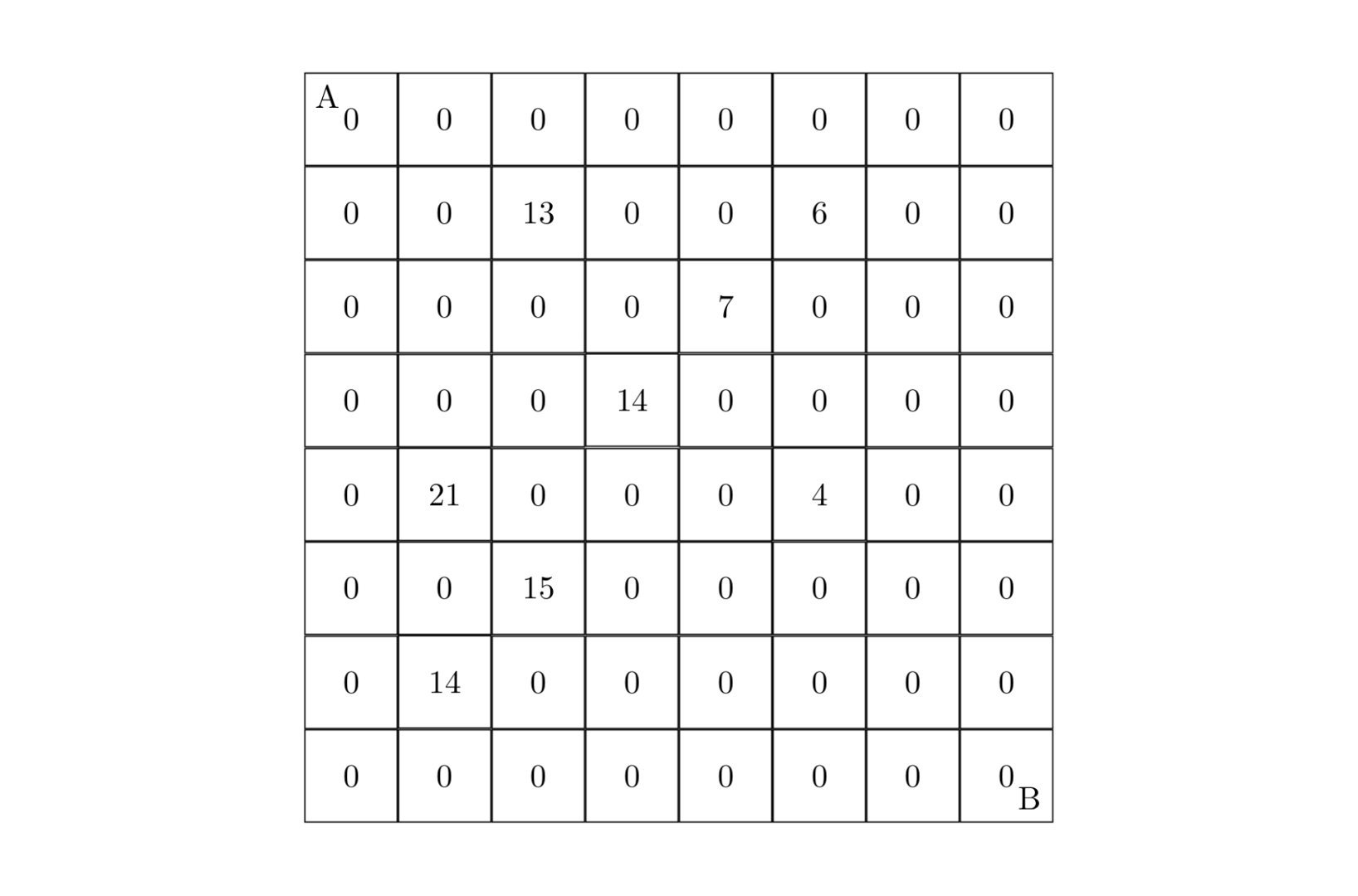
设有 的方格图 ，我们将其中的某些方格中填入正整数，而其他的方格中则放入数字 。如下图所示（见样例）:

某人从图的左上角的 点出发，可以向下行走，也可以向右走，直到到达右下角的 点。在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字 ）。 此人从 点到 点共走两次，试找出 条这样的路径，使得取得的数之和为最大。

输入的第一行为一个整数 （表示 的方格图），接下来的每行有三个整数，前两个表示位置，第三个数为该位置上所放的数。一行单独的 表示输入结束。

数据范围：。

好家伙，两次DP？？？我们就选择用一个DP数组记录两条路径，同时遍历寻找最优解，最后输出即可。

状态表示就很明朗了，全集是两条从点 走到点 的路径可能性，属性是max。在状态计算方面，我们选用dp[i1][j1][i2][j2]表示第一条路线从 走到了当前的 ；第二条路线从 走到了当前的 。这样来看，我们就只需要判断路径重合的情况：当 时两条路径有可能重合。既然是「有可能」，那也就是说存在误判的情况失手了口牙。这里，y总引入了一个新变量 ，并使上式中的 ，如此操作，就可以删去dp数组的 和 ，转而用dp[k][i1][i2]表示，移项可得 。因为DP操作仅限于这个 的方阵中，所以取值范围 ，最大值就是到达右下角的 ，因此 （严格来说， ）。关于 的循环应该是从 开始一直到 才对。

然后考虑状态之间的转移，就需要找到当前状态和上一个状态之间的联系。dp数组存储了两条路径，第一条路径可能从左侧过来、同时第二条路径也可能从左边过来；第一条从左边来、第二条从上边来；第一条从上边来、第二条从左边来；最后是两条都从上边来的情况。我们显然需要计算出这四种情况的状态后对所有状态联合取最大值，以第一种情况为例：两条都从左边来，那么 就是从 来的；如果是第二种情况，那么 由 过来、 由 来，该情况写成转移方程就是dp[k][i1][i2] = max(dp[k][i1][i2], dp[k - 1][i1][i2] + w[i1][j1] + w[i2][j2])。

最后是重合路径的问题，当 唯一确定， 时， ，所以 ，两点重合。所以当循环内出现 的情况时直接抛除就好。状态转移方程里面也不能按w[i1][j1] + w[i2][j2]加和而是需要按w[i1][j1]进行累加。注意判断 和 是否都在地图范围内。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

#include <bits/stdc++.h>

#define N 15
using namespace std;

int dp[2 * N][N][N], w[N][N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;
    int x = 1, y = 1, d = 1;
    while (x || y || d) {
        // 谨防毒瘤数据权值出成0！！！
        // 我也不知道权值会不会是0……保险保险
        cin >> x >> y >> d;
        w[x][y] = d;
    }
    for (int k = 2; k <= 2 * n; k++) {                                          // 注意k的取值范围
        for (int i1 = 1; i1 <= n; i1++) {
            for (int i2 = 1; i2 <= n; i2++) {
                int j1 = k - i1, j2 = k - i2;
                if (1 <= i1 <= n && 1 <= i2 <= n && 1 <= j1 <= n && 1 <= j2 <= n) {
                    int val = (i1 == i2) ? w[i1][j1] : w[i1][j1] + w[i2][j2];   // 判断是否重合
                    int &current = dp[k][i1][i2];                               // 设置引用缩减码量
                    current = max(current, dp[k - 1][i1][i2] + val);            // 两条都从上边来
                    current = max(current, dp[k - 1][i1][i2 - 1] + val);        // 第一条从上边来，第二条从左边来
                    current = max(current, dp[k - 1][i1 - 1][i2] + val);        // 第一条从左边来，第二条从上边来
                    current = max(current, dp[k - 1][i1 - 1][i2 - 1] + val);    // 两条都从左边来
                }
            }
        }
    }
    cout << dp[2 * n][n][n] << endl;
    return 0;
}

总用时： 记录

来都来了，顺便放一下传纸条的代码，两道题思路是相同的（状态转移方程都不需要改！），但是读入有点恶心，一定注意读入问题！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

#include <bits/stdc++.h>

#define N 110
using namespace std;

int dp[2 * N][N][N], w[N][N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;
    // 注意读入问题
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            int d;
            cin >> d;
            w[i][j] = d;
        }
    }
    for (int k = 2; k <= m + n; k++) {                                          // 注意k的取值范围
        for (int i1 = 1; i1 <= n; i1++) {
            for (int i2 = 1; i2 <= n; i2++) {
                int j1 = k - i1, j2 = k - i2;
                if (1 <= i1 <= n && 1 <= i2 <= n && 1 <= j1 <= m && 1 <= j2 <= m) {
                    int val = (i1 == i2) ? w[i1][j1] : w[i1][j1] + w[i2][j2];   // 判断是否重合
                    int &current = dp[k][i1][i2];                               // 设置引用缩减码量
                    current = max(current, dp[k - 1][i1][i2] + val);            // 两条都从上边来
                    current = max(current, dp[k - 1][i1][i2 - 1] + val);        // 第一条从上边来，第二条从左边来
                    current = max(current, dp[k - 1][i1 - 1][i2] + val);        // 第一条从左边来，第二条从上边来
                    current = max(current, dp[k - 1][i1 - 1][i2 - 1] + val);    // 两条都从左边来
                }
            }
        }
    }
    cout << dp[m + n][n][n] << endl;
    return 0;
}

总用时： 记录

子序列型 线性DP

子序列指在原序列中，在不改变元素之间的相对顺序的前提下，从中抽取出的元素组成的序列。例如数列1 4 5 6 7 8，1 5 7 8就是原序列的一个长度为 的子序列，特殊地，原序列本身也是它的一个子序列。根据子序列元素之间的大小关系，大致分为“上升型”、“不下降型”、“下降型”和“不上升型”，分别对应前后元素是小于、小于等于、大于和大于等于的关系。在引入第二个序列的情况下，问题还可以进阶成为“公共子序列问题”，公共子序列正如其名：若某序列是两个及以上的序列的子序列，那么这个序列就是后者的公共子序列。

线性DP可以用于求解符合以上特点的子序列的最长长度，在 的复杂度内得出结果，某些子序列计算可以通过贪心进行优化，最快可到 级别。在竞赛中通常以英文缩写称之，例如最长上升子序列LIS、最长公共子序列LCS和二者的融合——最长上升公共子序列LCIS问题。

洛谷 B3637 最长上升子序列 LIS

题目传送门：B3637 最长上升子序列

难度：普及-

来源：NOIp 提高组  2004

这是一个简单的动规板子题。

给出一个由 个不超过 的正整数组成的序列。请输出这个序列的最长上升子序列的长度。

最长上升子序列是指，从原序列中按顺序取出一些数字排在一起，这些数字是逐渐增大的。

甚至你有可能都没见过B开头的洛谷题……在题库上端的“入门与面试”选项卡里，你可以找到B开头的题

在子序列DP的思考中，通常对DP的全集有一个比较跳脱常理的思维，通常让dp[i]作为以a[i]结尾的某类型子序列的最长长度。而子序列问题的状态集合属性也自然而然就是max了。

那么假设此时DP进行到了第 项（ ），为了得出状态转移方程，我们聚焦到dp[i]的前一项，也就是dp[i - 1]。搞明白在什么情况下dp[i - 1]才能转化为dp[i]。不难发现，解决LIS问题，核心就是保证后一项的数严格大于前一项的数。于是当 时，我们就可以将 纳入最长子序列的计数中，也就是dp[i] = dp[i - 1] + 1。

对于dp数组初始化，因为每个元素本身就是原序列的一个长度为1的上升子序列，所以必须让dp数组的每个位置都初始化成 。在最后，因为我们也不知道以第几个元素为结尾的上升子序列可以取到最大长度，因此我们还需要从头到尾扫一遍取最大值。代码给出：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <bits/stdc++.h>

#define N 5010
using namespace std;

int dp[N], a[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) dp[i] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    int ans = -1;
    for (int i = 1; i <= n; i++) ans = max(ans, dp[i]);
    cout << ans << endl;
    return 0;
}

总用时： 记录

洛谷 P1091 合唱队形

题目传送门：这里

难度：普及/提高-

位同学站成一排，音乐老师要请其中的 位同学出列，使得剩下的 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 位同学从左到右依次编号为 … ，他们的身高分别为 … ，则他们的身高满足 … 。

你的任务是，已知所有 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入共二行。

第一行是一个整数 （），表示同学的总数。

第二行有 个整数，用空格分隔，第 个整数 （）是第 位同学的身高（厘米）。

对于全部的数据，保证有 。

样例输入

1 2	8 186 186 150 200 160 130 197 200

样例输出

4

要想出列的人最少，留下的人必须最多！废话

那么如何保证留下的人最多呢？读题，要求是让整个队形变成先升后降的形式。我们不妨将样例输入进行一次可视化：

题目想让我们把这张图变成左边上升右边下降的样子，形状酷似山峰，因此我称之为山峰模型。联系到刚才所说，需要让留下的人最多。我们在选择C位同学时就需要注意一下，让他左侧留下的人最多、而不是一定要让最高的站中间。这下就很明朗了，我们先正向（从左至右）做一遍LIS问题，就知道让哪个人站C位可以使得Ta左边的人出列最少。那么还差右边的人，怎么办呢？我们会发现如果将整个序列倒序一下（水平翻转），那么原先的右侧就变为现在的左侧，原先让右侧单调下降，现在就变成了左侧单调上升，也就是和处理左侧同样的思路。于是我们就对原序列跑一遍LIS，再对反向的序列跑一遍LIS。最后 统计一下每个点跑两次LIS后结果的总和（对应留下的人的人数），找出总和最大的那个就好了。至此我们已经成功将这个问题转化为两次异向LIS问题了！

最后有一点小细节，是关于最终结果的。样例输入的原理是将中间那个身高两米（176cm小矮个瑟瑟发抖）的设为C位，让左侧150cm和任意一个186cm、右侧197cm和200cm的人出列（注意是保证严格上升，因此若连续二者身高相等则不计入LIS计数）。答案就是 。可以发现中间200cm的同学，正向LIS的结果是 、反向LIS的结果是 。但是 ，少了一个人去哪了——这是因为正反向LIS都算入了一次那个两米的同学，根据容斥原理，多算一次，就要减去一次，实际留下的人数是 人，答案就是 人。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include <bits/stdc++.h>
#define rev(x) n - x + 1
#define N 5010
using namespace std;

int dp[N], rev_dp[N];
int a[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) {
        dp[i] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    reverse(a + 1, a + n + 1);
    for (int i = 1; i <= n; i++) {
        rev_dp[i] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) rev_dp[i] = max(rev_dp[i], rev_dp[j] + 1);
        }
    }
    int ans = -1;
    for (int i = 1; i <= n; i++)
        ans = max(ans, dp[i] + rev_dp[rev(i)]);
    cout << n - (ans - 1) << endl;
    return 0;
}

总用时： 记录

洛谷 P2782 友好城市

题目传送门：这里

难度：普及/提高-

有一条横贯东西的大河，河有笔直的南北两岸，岸上各有位置各不相同的 个城市。北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不相同。每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。编程帮助政府做出一些批准和拒绝申请的决定，使得在保证任意两条航道不相交的情况下，被批准的申请尽量多。

输入第一行，一个整数 ，表示城市数。

输入第二行到第 行，每行两个整数，中间用一个空格隔开，分别表示南岸和北岸的一对友好城市的坐标。

输出仅一行，一个整数，表示政府所能批准的最多申请数。

样例输入

1 2 3 4 5 6 7 8

7 22 4 2 6 10 3 15 12 9 8 17 17 4 2

样例输出

1

4

数据范围

• 对于 的数据，，。
• 对于 的数据，，。

样例看起来不是那么直观，考试时可以考虑用画图软件增强样例可读性，样例画成图就是下边这样：

样例输出为 ，意味着我们需要删去 条边，分别是边 、 和 。为了探寻普遍规律，我们分离部分相交的航道来看一看，寻找相交线与河岸两头编号的规律。

我将北岸城市所连接的南岸城市的编号以深蓝色字体标在了对应北岸城市的下方，这下就可以看出端倪了：北岸城市从左至右，当底部蓝色数字单调上升时，航线不会交叉；反之若出现破坏单调性的蓝色数字，就代表航线交叉。但这个不完全归纳出来的结论还是欠缺证据支撑，对于北岸城市，编号单调递增，也就是说若航线以北岸城市为起点，那么起点处航线是绝对不会相交的；但是对于整条航线，它在整条河上是连续不断的——比如上图中蓝色数字 和 ，表明北四号城市连接了一个很远的南二十二号城市；下一个是北十二号城市，连接南十五号城市。整条航线在河上连续不断，意味着航线 总会在河上有一个正对南四~二十二号城市的点，此时当航线 出现时，它们总会在某处相交。南岸证明同理。至此就证明了这个单调递增规律的问题，因此我们就想办法把南北岸城市的编号一一对应起来，接着跑一遍LIS，就可以解出答案了。

这里介绍一下C++的pair：pair是一个二元组，在定义时传入第一参数和第二参数的数据类型，类似于vector的定义，它们也用一对尖括号包裹。特定类型的pair，例如pair<int, int>、pair<double, double>、pair<float, float>等，在sort函数中可以自动按第一参数排序。这里我们选择双int型pair来存储南北城市的对应关系。代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <bits/stdc++.h>

#define N 200010
using namespace std;

typedef pair<int, int> coord;

int dp[N];
coord a[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i].first >> a[i].second;
    sort(a + 1, a + n + 1);
    for (int i = 1; i <= n; i++) {
        dp[i] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j].second < a[i].second) dp[i] = max(dp[i], dp[j] + 1);
        }
    }
    int res = -1;
    for (int i = 1; i <= n; i++) res = max(res, dp[i]);
    cout << res << endl;
    return 0;
}

总用时：TLE 记录

注意到这里的数据范围：前50%没有问题，重点是后50%，它们的 。LIS的时间复杂度是 ，早T飞了。不过AcWing对应的例题的数据没有洛谷上这么强，在AcWing 1012 友好城市里可以用LIS代码AC，后者的数据范围是 。要想通过洛谷的友好城市，就必须用贪心等其他优化方式将时间复杂度降到对数级别才行……画大饼画大饼

AcWing 1016 最大上升子序列和

题目传送门：这里

难度：简单

最大上升子序列和，又称MASS（Maxiumum Ascending Subsequence Sum）问题。是LIS问题的一种变式，它不再是只局限于上升子序列的最长长度、而是开始关注选定子序列的元素之和。MASS问题其实可以拆分为两个子问题求解，其一是上升子序列问题、其二是最大和问题。上升子序列无需多言，其本质是在循环内加上判断a[j] < a[i]来累加合法解个数。因此，如果想要再融合进最大值问题，我们就需要在状态转移那里改一下代码：考虑到LIS问题的dp数组记录的是合法解的个数，而每次找到一组合法解，答案只会累加 ；对于MASS问题，每次找到一组合法解，需要累加的是元素本身的权值，特殊情况，单元素组成子序列时，答案就是它本身的权值，因而初始化时需要把dp[i]设置成a[i]才对。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <bits/stdc++.h>

#define N 1010
using namespace std;

int dp[N], a[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) {
        dp[i] = a[i];
        for (int j = 1; j < i; j++) {
            if (a[j] < a[i]) dp[i] = max(dp[i], dp[j] + a[i]);
        }
    }
    int res = -1;
    for (int i = 1; i <= n; i++) res = max(res, dp[i]);
    cout << res << endl;
    return 0;
}

总用时： 记录

AcWing 1010 拦截导弹

题目传送门：这里

难度：简单

来源：NOIp 提高组  1999

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度，计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入仅一行，若干个整数，中间由空格隔开。

输出包含两行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

样例输入

1	389 207 155 300 299 170 158 65

样例输出

1 2

6 2

保证导弹数量不超过

同样画图理解样例抽象派画师又要登场喽！

那么怎么做才是样例输出的解呢？很明显，把207和155单独提出来作为一个新系统；剩下的作为一个系统。也就是说最多能拦截除开207和155的其他六枚导弹，而新开了一个系统，所以总共是两个系统。

乍一看这很像一个求解最长单调不上升子序列的问题，但是它居然让我们求出系统的数量，这就很棘手了……所以我们需要一个两头兼顾的方法来解题：

当我们拿到这个序列，之后只会进行两种操作：第一种是将某个数接到已有的子序列之后、第二种是新开一个子序列。考虑到我们的目标之一是让新开的子序列尽量小，那我们就需要尽可能缩减第二种操作的执行次数——让尽可能多的数被归入子序列中，这样的话我们就需要让插入的数和插入前队尾的数尽可能接近才是，如此会让系统的利用率最大化（如果你是舰长总司令，拿到这种系统，你肯定不会轻易地让它拦截很低的导弹，这样只会降低系统利用率）。当然，我们也希望打头的元素尽量大一些，这样才会容纳进更多的元素。诶？这不就是贪心的思路吗？为了方便阅读，做归纳如下：

贪心过程：从前到后扫描每个数，并且：

• 如果现有的所有子序列的结尾都小于这个数，显然不能插入，就开新序列（创建新系统）
• 如果存在合法（符合题意且当前元素可插入队尾）的子序列，遍历队尾元素，找到和当前元素最相近的那个队尾对应的子序列插入

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include <bits/stdc++.h>

#define N 1010
using namespace std;

int dp[N], a[N], b[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n = 1;
    while (cin >> a[n]) n++;
    n--;
    int lis = -1;
    for (int i = 1; i <= n; i++) {
        dp[i] = 1;
        for (int j = 1; j < i; j++) {
            if (a[j] >= a[i]) dp[i] = max(dp[i], dp[j] + 1);
        }
        lis = max(lis, dp[i]);
    }
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        int tmp = 0;
        while (tmp < cnt && b[tmp] < a[i]) tmp++;
        b[tmp] = a[i];
        if (tmp >= cnt) cnt++;
    }
    cout << lis << endl << cnt << endl;
    return 0;
}

总用时： 记录

AcWing 897 最长公共子序列 LCS

题目传送门：这里

难度：简单

最长公共子序列，又称LCS（Longest Common Subsequence）问题。这个问题要求我们解出两个不相关序列的最长的公共子序列长度。公共子序列，顾名思义：假设有两个序列 和 ，它们的公共子序列 既是 的子序列、也是 的子序列。搞明白了公共子序列的定义，我们来解题：

给定两个长度分别为 和 的字符串 和 ，求既是 的子序列又是 的子序列的字符串长度最长是多少。

输入输出

第一行包含两个整数 和

第二行包含一个长度为 的字符串，表示字符串 。

第三行包含一个长度为 的字符串，表示字符串 。

字符串均由小写字母构成。

输出一个整数，表示最大长度。

数据范围

样例输入

1 2 3

4 5 acbd abedc

样例输出

1

3

这道题就和前面的LIS问题不一样了，人家是在一个序列里操作，现在变成了两个序列。我们在选取状态的表示时就要换一种思维了。假设dp[i][j]表示的是以 序列中前 个元素和 序列中前 个元素组成的最长公共子序列的长度。根据公共子序列的定义，我们可以抛出如下两种情况：

1. 当 时，证明元素 不能被选入到公共序列中（数据不相同，即不满足“公共”）
2. 当 时，证明元素 可以被选入到公共序列中

第一种情况，大问题被切分了，我们要找到距离它最近的一个合法的公共子序列。我们先后尝试删去当前的 和 ，然后看一下得到的结果是否是合法的公共子序列，类似于一个递归的过程。因此dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])。

第二种情况，我们选入了 和 ，注意到 ，我们只需要选一个进入公共子序列即可，因此长度也只需累加 。类比第一种情况的思路，我们往回查找距离当前状态最近的一个合法的公共子序列，也就是尚未选中 或 时的状态。得到dp[i][j] = dp[i - 1][j - 1]。

综上所述：

这个 看起来就高级多了

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

#include <bits/stdc++.h>

#define N 1010

using namespace std;

int dp[N][N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;

    string a, b;
    cin >> a >> b;

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i - 1] == b[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
            else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}

总用时： 记录

AcWing 272 最长公共上升子序列 LCIS

题目传送门：这里

难度：中等

最长上升公共子序列，听名字就能看出是最长上升子序列和最长公共子序列的结合体。如此高级的题目自然有非常高级的方法来解决，请看下边例题：

熊大妈的奶牛在小沐沐的熏陶下开始研究信息题目。

小沐沐先让奶牛研究了最长上升子序列，再让他们研究了最长公共子序列，现在又让他们研究最长公共上升子序列了。

小沐沐说，对于两个数列 和 ，如果它们都包含一段位置不一定连续的数，且数值是严格递增的，那么称这一段数是两个数列的公共上升子序列，而所有的公共上升子序列中最长的就是最长公共上升子序列了。

奶牛半懂不懂，小沐沐要你来告诉奶牛什么是最长公共上升子序列。

不过，只要告诉奶牛它的长度就可以了。

数列 和 的长度均不超过 。

---

输入第一行包含一个整数 ，表示数列 的长度。

输入第二行包含 个整数，表示数列 。

输入第三行包含 个整数，表示数列 。

输出一个整数，表示最长公共上升子序列的长度。

状态表示和上边LCS差不太多，这里的dp[i][j]表示的是 序列的前 个元素与 序列中前 个元素组成、且以 结尾的最长上升公共子序列的长度。看起来只是多了一条限制信息——“以 结尾”。

首先套用LCS的思想（LIS什么时候都可以求，但求出的LIS不一定符合LCS的定义，因此LCS求解优先级大于LIS）：

• 当 时，当前子序列不允许 的加入（没有满足是LCS序列的大前提）
• 当 时，当前子序列中加入 。枚举 分析是否满足LIS序列的要求。

第一点不再赘述，如果连LCS都不是，更不用说LCIS了。重要的是第二点，当 和 已经满足公共的前提时，就需要接着处理“上升”的关系。很明显，以不同的 结尾得出的LIS的解是不同的，类似于先前 求解LIS的思路，我们从 枚举到 来记录全局最大值，因为以 、 …… 结尾的上升子序列长度是不一定相同的。在这里，我们枚举第二变量 ，使得上升子序列求得最大值。这回可以套LIS代码，效果是在求解LCS的同时求解LIS，合起来就是LCIS！

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

#include <bits/stdc++.h>

#define N 3010

using namespace std;

int dp[N][N];
int a[N], b[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;

    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) cin >> b[i];

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            dp[i][j] = dp[i - 1][j];
            if (a[i] == b[j]) {
                for (int k = 1; k <= j; k++) {
                    if (b[j] > b[k]) {
                        dp[i][j] = max(dp[i][j], dp[i - 1][k] + 1);
                    }
                }
                if (!dp[i][j]) dp[i][j] = 1; // 切记，LIS问题的初值是1，也就是说单元素LIS的值是1
            }
        }
    }
    int ans = -1;
    for (int i = 1; i <= n; i++) ans = max(ans, dp[n][i]);
    cout << ans << endl;
    return 0;
}

TLE了~ 记录

y总当时做的时候估计只有10个比较弱的数据，现在可能是加上了3个强数据，卡掉了 的朴素做法

注意到上边这段代码是在LCS的双层循环里又套了一层属于LIS的循环，复杂度是 的，极其之抽象。数据范围是 ，最坏情况下要跑几十秒……那么如何优化？对照数据范围，我们的目标是将算法复杂度降到 $ 及以下。优化思路如下：

优化从第三层循环入手，如果找到一种方法，让最大值的获取变成 ，那么整体复杂度就会降到 。看起来不错。因为整体的循环的大前提是 ，循环的目的是找到当 时dp数组里存储的最大值，那么维护最大值maxx，当 时更新值就可以了。根据等式，有 ，因此当 时就可以更新maxx为max(maxx, dp[i - 1][j])。

优化代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

#include <bits/stdc++.h>

#define N 3010
using namespace std;

int dp[N][N], a[N], b[N];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);

	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) cin >> b[i];

	for (int i = 1; i <= n; i++) {
		int maxx = 0; // 注意从0开始 
		for (int j = 1; j <= n; j++) {
			dp[i][j] = dp[i - 1][j];
			if (a[i] == b[j]) dp[i][j] = maxx + 1;
			else if (a[i] > b[j]) maxx = max(maxx, dp[i - 1][j]);
		}
	}
	int res = -1;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			res = max(res, dp[i][j]);
		}
	}
	cout << res << endl;
	return 0;
}

总用时： 记录

当然，这段代码实际上只使用到了dp[i - 1][j]一个前驱状态，可以用滚动数组法把dp数组压缩至一维的。滚动数组法将在后边介绍。

补 贪心优化子序列问题

正常做子序列问题的时候，由于要枚举每一个可能的状态，因此需要循环 级别次，时间复杂度也就来到了惊人的 （大多数题目的暴力算法都是这个复杂度），当 时就TLE了，更别说更加毒瘤的数据了……好在对于最值子序列问题，人们提出了贪心法，可以将复杂度降落到对数级别，一般是 （某些题用特定的数据结构还可以降到 复杂度）。是一种极其高效的优化方式。

之前我们T掉了一道题，洛谷 P2782 友好城市，TLE的主要原因是求解LIS时使用了 的朴素DP法。那我们就回填之前挖出来的大坑，试着用 的贪心法求解LIS。

假设原序列为a，len为LIS问题的解，p数组是维护的最长上升子序列，q作为操作序列暂存（不是最终结果）。LIS问题的贪心思路如下：

• 将第一个元素压入q中，让len累加 ，并且让q[1] = a[1]。此时len = 1
• 对于每一个新元素x，如果x > q[len]，让q[++len] = x，并扩展p
• 反之，在q数组中找到第一个大于等于x的元素y，并将y替换成x

第一点很显然是第二点在q数组为空时（刚开始求解）的特殊情况，我们只看第二和第三点。当新元素大于队尾，意味着它完全有资格进入最长上升子序列的行列中，因此压入队尾；但是当这个元素不再大于队尾，而是一个较小的值，就要好好考虑一下了……

通常，我们在求解的中途希望相邻的两个候选元素相差尽可能小，这样才有更多的空间存更多的值，从而达到最长。在这种情况下，我们称替换用的元素比被替换的元素有更好的潜力值。当然，寻找替换元素的下标无疑是一个耗时的工作，考虑到q数组严格递增的性质，我们不妨采用二分查找（或者lower_bound()函数）找到指定元素的下标：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

#include <bits/stdc++.h>
#define N 100010
using namespace std;

int a[N], q[N], p[N];
int len = 0;
int main() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	for (int i = 1; i <= n; i++) {
		if (a[i] > q[len]) q[++len] = a[i];
		else {
			int idx = lower_bound(q + 1, q + 1 + len, a[i]) - q; // 在[1,len]区间内查找待替换目标的下标，适用于单调上升序列
			//int idx = upper_bound(q + 1, q + 1 + len, a[i], greater<int>()); // 适用于单调下降序列 
			q[idx] = a[i];
		}
	}
	cout << len << endl;
	return 0;
}

既然我们已经学会了这个优化方法，可以拿它来切题了。

洛谷 P1020 导弹拦截

题目传送门：这里

难度：普及/提高-

来源：NOIp 提高组  1999

实际上是这道题的洛谷数据加强版……

实现思路和前面AcWing 1010一个道理，这里我们加上LIS的优化。注意根据题目，我们需要求一个最长不上升子序列的长度，那么用到上边优化代码里被注释的那一行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

#include <bits/stdc++.h>

#define N 100010
using namespace std;

int a[N], b[N], q[N];
int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n = 1;
    while (cin >> a[n]) n++;
    n--;
  
    int lis = 0;
    q[++lis] = a[1];
    for (int i = 2; i <= n; i++) {
	if (a[i] <= q[lis]) q[++lis] = a[i];
	else {
	    int idx = upper_bound(q + 1, q + lis + 2, a[i], greater<int>()) - q;
	    q[idx] = a[i];
        }   
    }

    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        int tmp = 0;
        while (tmp < cnt && b[tmp] < a[i]) tmp++;
        b[tmp] = a[i];
        if (tmp >= cnt) cnt++;
    }
    cout << lis << endl << cnt << endl;
    return 0;
}

总用时： 记录

这里把能AC友好城市的代码一并贴在这里，因为这道题需要求上升子序列最长长度，我们使用的是lower_bound()：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <bits/stdc++.h>

#define N 200010
using namespace std;

typedef pair<int, int> coord;

int dp[N];
coord a[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i].first >> a[i].second;
    sort(a + 1, a + n + 1);
	int lis = 0;
	for (int i = 1; i <= n; i++) {
		if (dp[lis] < a[i].second) dp[++lis] = a[i].second;
		else {
			int idx = lower_bound(dp + 1, dp + 1 + lis, a[i].second) - dp;
			dp[idx] = a[i].second;
		}
	}
    cout << lis << endl;
    return 0;
}

总用时： 记录

背包DP 基础

背包问题是一种组合优化问题，大多数时候用来求解有限定条件的最值选择问题。一般的背包问题会给出这个背包所能承受的“最大容量”，并同时列出各物品的体积和价值，要求从中选择物品，使得选择的物品在不超过背包限定容量的情况下，总价值最大。根据物品的选法，可以大致分成几类：0/1背包、完全背包、多重背包等。

0/1背包

在0/1背包问题中，限制每个物品至多被选择一次，因此对于某个物品，只有“选”和“不选”两种情况。因此得名0/1（不选为0，选为1）。

对于背包问题的空间优化（滚动数组优化）将在后边统一涉及。

洛谷 P1048 采药

题目传送门：这里

难度：普及-

来源：NOIp 普及组    2005

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

---

输入：第一行有 个整数 （）和 （$1 M

T$ 代表总共能够用来采药的时间， 代表山洞里的草药的数目。

接下来的 行每行包括两个在 到 之间（包括 和 ）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出：在规定的时间内可以采到的草药的最大总价值。

在背包问题中，通常让dp数组带上题目的限制条件。在这里，我们令dp[i][j]表示选择前 个物品且此时所选物品总容量不超过 （剩余可用容量）时的最大价值。属性自然是max。假设第 个物品价值是 、体积是 。

因为每个物品至多选择一次，分两种情况讨论——“选”或者是“不选”第 个物品。

如果不选这个物品，相当于这个状态不存在，因此第二维不需要更新，相当于是只选择了前 个物品的情况，也就是dp[i][j] = dp[i - 1][j]；但如果选择了这第 个物品，我们就需要观察分析一下数组的变化了——这个状态很明显，是从它的前驱dp[i - 1][j]转移过来的。那么在选择了物品 之后，背包的剩余容量自然就是 了，并且总价值会增加 ，为了保证状态数组的最值，对“选”和“不选”两种情况取最大值，也就是dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i])。注意，若当前的容许最大容量小于当前物品的体积时，就无法选择这个物品，相当于不选时的情况，加上循环内特判就行了。

当我们把这道题里的时间想象成背包问题的总容量，题目就变成了一个0/1背包模板题了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include <bits/stdc++.h>

#define N 1010
using namespace std;

int dp[N][N], w[N], v[N];
int main() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);

	int t, m;
	cin >> t >> m;
	for (int i = 1; i <= m; i++) {
		cin >> v[i] >> w[i];
	} 
	for (int i = 1; i <= m; i++) {
		for (int j = 1; j <= t; j++) {
			if (j >= v[i]) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);
			else dp[i][j] = max(dp[i][j], dp[i - 1][j]);
		}
	}
	cout << dp[m][t] << endl;
	return 0;
}

总用时： 记录

完全背包

类比0/1背包每样物品至多选择一次的策略，完全背包则是让每样物品的选择次数上限变成了正无穷。也就是说我们可以抓住一个物品暴风吸入，只要保证在限定容量内装入最大价值的物品即可。

洛谷 P2722 总分 Score Inflation

题目传送门：这里

难度：普及-

来源：USACO

选手在我们 USACO 的竞赛中的得分越多我们越高兴。

我们试着设计我们的竞赛以便人们能尽可能的多得分,这需要你的帮助。

我们可以从几个种类中选取竞赛的题目，这里的一个“种类”是指一个竞赛题目的集合，解决集合中的题目需要相同多的时间并且能得到相同的分数。

你的任务是写一个程序来告诉 USACO 的职员,应该从每一个种类中选取多少题目，使得解决题目的总耗时在竞赛规定的时间里并且总分最大。

---

输入的第一行是用空格隔开的两个整数，分别代表竞赛时间 和题目类 。

第 到第 行，每行两个用空格隔开的整数，第 行的整数 分别代表解决第 类题得到的分数和需要花费的时间。

既然是某一类题目，那么这一类题目可以重复选择

输出一行一个整数，代表最大的总分。

---

对于 的数据，保证 $1 n, m ^4

$，。

状态的表示和上面0/1背包是相同的，不再多说。重要的是推导状态，还是分为“选”和“不选”两种情况，如果不选，和上面一样，就是dp[i - 1][j]；但是如果选择这个物品，那就需要千万注意了：

我们找到上一步的状态，是dp[i - 1][j]吗？——显然欠缺考虑，万一第 个物品已经选择过不止一次呢？使用这个状态相当于直接放弃了先前选择过数次的物品 ，有悖于集合划分“不重不漏”的基本原则。假设当前状态已经减去了 ，变成了dp[i][j - v[i]] + w[i]，那么上一个状态就是dp[i][j]。这是因为上一个状态可能已经选取了多个物品 ，我们不能放弃掉原先存储的状态，就可以换个思路，直接在原有基础上，再选一个物品 。因此该情况下，dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i])。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <bits/stdc++.h>

#define N 10010
using namespace std;

int dp[N][N], w[N], v[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t, m;
    cin >> t >> m;
    for (int i = 1; i <= m; i++) {
        cin >> w[i] >> v[i];
    }
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= t; j++) {
            if (j < v[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j]);
            else dp[i][j] = max(dp[i - 1][j], dp[i][j - v[i]] + w[i]);
        }
    }
    cout << dp[m][t] << endl;
    return 0;
}

总用时：MLE 记录

原因是当数组占满时，整个内存将会来到，题目限制125MB，爆了三倍还多。后文会介绍滚动数组优化法后会提供能AC此题的正解代码。

多重背包

多重背包的物品选择策略可以说是最接近日常生活的一种了，它规定某种物品只能选择至多 次。因此它介于0/1背包和完全背包之间，状态转移也更加复杂，但更具普遍性。接下来引入一道模板题来感受多重背包的解题思路。

洛谷 P1833 樱花

题目传送门：这里

难度：普及/提高-

爱与愁大神后院里种了 棵樱花树，每棵都有美学值 。爱与愁大神在每天上学前都会来赏花。爱与愁大神可是生物学霸，他懂得如何欣赏樱花：一种樱花树看一遍过，一种樱花树最多看 遍，一种樱花树可以看无数遍。但是看每棵樱花树都有一定的时间 。爱与愁大神离去上学的时间只剩下一小会儿了。求解看哪几棵樱花树能使美学值最高且爱与愁大神能准时（或提早）去上学。

---

输入：共 行：

第 行：现在时间 （几时：几分），去上学的时间 （几时：几分），爱与愁大神院子里有几棵樱花树 。这里的 ， 格式为：hh:mm，其中 ，，且 均为正整数。

第 行到第 行，每行三个正整数：看完第 棵树的耗费时间 ，第 棵树的美学值 ，看第 棵树的次数 （ 表示无数次， 是其他数字表示最多可看的次数 ）。

输出：只有一个整数，表示最大美学值。

---

数据：（即开始时间距离结束时间不超过 $1000

$ 分钟），。保证 为同一天内的时间。

这道题怎么降黄了？

如何处理这种个数有限的物品呢？常规的思路是将一个价值为 ，个数为 的物品拆分成 个个体，对于整体，使用0/1背包的方式求解即可；或者也可以在选择物品时采用计数+特判，当容量不够或达到上限时退出循环即可。但是限于题目要求，这种方法在大多数情况下是无法完美通过测试点的，尤其是当物品种类数和物品件数的乘积过大时，光是拆分这一项就足够超时了。因此我们需要一个更为高效的拆分法来拆分这些物品。

想象这样一个情境，你的面前放着 个苹果。但是你只需要其中的 颗，你希望将它们装到 个盒子里自己带走，请问 之间有什么关系？

---

根据情境，我们就需要将 分为 个数的和，当 是 的倍数时还好说，那万一不是呢？能不能提出一种通用解法？

学OI的人们都知道，世界上所有的数都可以用一个01串表示，也就是二进制下的表示，和十进制一样按位计数。比如：；。那么问题就解决了， 就是 的二进制表示下 的个数（解法不唯一）

对于物品 ，假设个数为 ，价值 ，体积 ，根据二进制表示法，对 进行二进制分解。只是这里和刚刚讲的二进制转化有些许不同，这里我们不停的用 的 次幂来作差，如此操作下来，。那么所有在区间 内的数就都可以表示出来了。