图论 欧拉图
图论起源 欧拉图
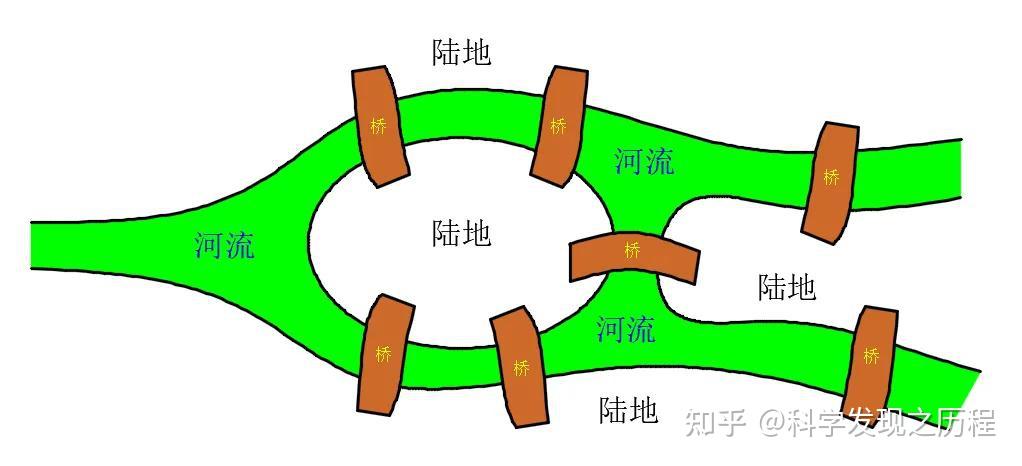
欧拉图的概念起源于18世纪的一个难题——“哥尼斯堡七桥问题”，问题是这样的：
有一条河上架设了如图所示的七座桥：
问如何在不重复经过某座桥的情况下走完这七座桥。
这个问题在当时难倒了一批人，有人写信给大神欧拉，请他帮忙解决这个问题。欧拉也是不负众望，经过一年的研究证明，发现这个七桥问题根本无解。在他的论文中提到了他的证明方法——将桥看作边、把陆地看作点，在一张图上研究问题。这也是数学图论思维的起源，因而欧拉图又被称作图论的起源。
现在看来，欧拉图可以看成一笔画问题。当这张图可以一笔画出，那么画出的路径就被称作欧拉路径；特殊地，当一笔画的起点和终点相同时，这个路径被称作欧拉回路。欧拉图基本可以分两个大类讨论——有向欧拉图和无向欧拉图。对于无向欧拉图来说，小学就已经涉及到了，判断方式如下：
- 整张图全为偶点（度数为偶数的点）
- 整张图只存在两个奇点（度数为奇数的点）
二者满足其一即可。那么对于有向欧拉图，因为涉及到边的方向，会稍微复杂一些：
- 图上每个点的入度均等于出度
- 图上只存在两个入度不等于出度的点——有一个点的入度比出度多 ，是图的起点；另一个点的出度比入度多 ，是终点
在求解某个欧拉路径/回路时，我们最常使用套圈法。这种方法基于对图的深度优先遍历，首先逮着一个路径向里搜索形成第一个回路，在回溯时如果发现某个点还有没被遍历过的边，就以它为起点向里搜索、并删除这条边。把回溯时走到的点记录起来，最后倒序输出就是合法回路（建议用栈）。
数组邻接表居然输给了 vector 存图？？？
void dfs(int u) { for (int i = nxt[u]; i < G[u].size(); i = nxt[u]) { nxt[u]++; dfs(G[u][i]); } path.push(u);}当然，如果题目要求按字典序输出路径，则需要对边排序。使用普通的数组邻接表显然是不方便的，那么考虑改用 vector。例如洛谷的模板题：
#include <bits/stdc++.h>#define N 100010using namespace std;
vector<int> G[N];stack<int> path;int indeg[N], outdeg[N];int nxt[N];int n, m;int cntS = 0, cntT = 0;
void dfs(int u) { for (int i = nxt[u]; i < G[u].size(); i = nxt[u]) { nxt[u]++; dfs(G[u][i]); } path.push(u);}
int main() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
cin >> n >> m; while (m--) { int u, v; cin >> u >> v; indeg[v]++; outdeg[u]++; G[u].push_back(v); } for (int i = 1; i <= n; i++) sort(G[i].begin(), G[i].end()); bool flag = true; int S = 1; for (int i = 1; i <= n; i++) { if (indeg[i] != outdeg[i]) { flag = false; if (outdeg[i] - indeg[i] == 1) cntS++, S = i; else if (indeg[i] - outdeg[i] == 1) cntT++; else { cout << "No" << endl; return 0; } } } if (!flag && cntS == cntT != 1) { cout << "No" << endl; return 0; } dfs(S); while (!path.empty()) { cout << path.top() << ' '; path.pop(); } return 0;}典例
洛谷 P2731 [USACO3.3] 骑马修栅栏 Riding the Fences
题目地址：P2731
题目难度：普及+/提高
Farmer John 每年有很多栅栏要修理。他总是骑着马穿过每一个栅栏并修复它破损的地方。
John 是一个与其他农民一样懒的人。他讨厌骑马，因此从来不两次经过一个栅栏。
John 的农场上一共有 个栅栏，每一个栅栏连接两个顶点，顶点用 到 标号（虽然有的农场并没有那么多个顶点）。一个顶点上至少连接 个栅栏，没有上限。两顶点间可能有多个栅栏。所有栅栏都是连通的（也就是你可以从任意一个栅栏到达另外的所有栅栏）。John 能从任何一个顶点（即两个栅栏的交点）开始骑马，在任意一个顶点结束。
你需要求出输出骑马的路径（用路上依次经过的顶点号码表示)，使每个栅栏都恰好被经过一次。如果存在多组可行的解，按照如下方式进行输出：如果把输出的路径看成是一个 进制的数，那么当存在多组解的情况下，输出 进制表示法中最小的一个 （也就是输出第一位较小的，如果还有多组解，输出第二位较小的，以此类推）。
输入数据保证至少有一个解。
输入格式：
第一行一个整数 ，表示栅栏的数目。
从第二行到第 行，每行两个整数 ，表示有一条栅栏连接 两个点。
输出格式：
共 行，每行一个整数，依次表示路径经过的顶点号。注意数据可能有多组解，但是只有上面题目要求的那一组解是认为正确的。
数据保证至少有一组可行解。
数据范围：
对于 的数据，。
根据题意，我们发现走过的路径恰好满足欧拉路径的定义（每个边只走一次）。又因为这道题保证有解，于是我们只需要套用模板求字典序最小的无向图欧拉路径并输出即可。这道题是无向图，用 vector 存又有些麻烦，我们可以用邻接矩阵，并从小到大枚举出边，可以达到一样的效果。
读入时需要特别注意，编号并不是严格从 开始、也不是在 结束——它不连续，因此需要预处理上下界，起点的初始值需要是图上的任意一个存在的编号。
void dfs(int u) { for (int i = 1; i <= n; i++) { if (g[u][i]) { g[u][i]--; g[i][u]--; dfs(i); } } path.push(u);}UVA10129 Play On Words
题目地址：UVA10129
题目难度：普及+/提高
输入个单词，是否可以把所有这些单词排成一个序列，使得每个单词的第一个字母可上一个单词的最后一个字母相同（例如）。每个单词最多包含个小写字母。输入中可以有重复的单词。
输入格式：
第一行为一个整数 ，代表有 组测试数据。
对于每组测试数据，第一行为一个整数 。接下来 行，每行读入一个字符串，每个字符串由 个小写字母组成，同一个字符串可能重复出现多次。
输出格式：
对于每组测试数据，如果能组成合法的单词链，输出一行
Ordering is possible.；否则输出一行The door cannot be opened.
很像之前遇见的一道 求负环+分数规划的题目 SP2885 WORDRING，只不过这道题没有要求最终字符串的首尾字符相同，我们只需判断能否把所有字符串都用上、组成一个单词链即可。注意到只要所有字符串能够不重不漏组成一个欧拉路径，该情况就是有解的，反之则无解。
更为详细的内容见：我的题解
支持与分享
如果这篇文章对你有帮助，欢迎分享给更多人或赞助支持！
部分内容可能已过时
