[奇技淫巧] 路径组合计数问题的线性递推解法
Prev 0. 引入
试看如下例题:
假设某小区的道路组成了一个
的网格结构(每条路就是一条横向或纵向排列的线段),小明住在网格左下角的 处,他想到达网格右上角的 处拜访好友。若小明采取最短路径移动,那么请问总共有多少条可能的路径?
非常明显,这是一道组合数的题目。根据题目条件,很容易知道最短路径的长度是
但是,如果我们将方格稍作改动,变成如下的形式:

就很欢愉了~
接下来讨论用线性 DP 的思想(线性递推)来解决包括以上两道经典例题以内的路径计数问题。
Div 1. 线性递推
开始之前先对“最佳路径”进行一个简单的定义:从给定终点到给定终点的最短路径;并定义“
这里的线性递推指的是由先前已知的状态,通过特定的计算方式得出当前状态的过程。在此类问题中表现为“用只走一步就可转移到当前格点的前驱格点的路径总数进行加法运算得到从起点开始并以当前格点为终点的路径总条数(满足路径为最佳路径)”。
空说比较晦涩,我们以上一节的第一个题为例实操一下:
例 1.1
问从
点到 点的最佳路径总数是多少?
刚刚我们已经从组合数角度探讨了本题的解法。接下来从线性递推的角度思考这道题。
考虑到“最佳路径”的定义,小明每次只能从某个格点移动到它上边或者是右边的点,换句话说:对于某个点(起点除外),小明只能从它左侧(最左一列除外)或者是下边(最下一行除外)相邻的点走过来。那么以当前点为终点的最佳路径条数就是左侧点的最佳路径条数与下边点的最佳路径条数之和。如此递推到
考虑到有一些特殊点(最左边一列、最下边一行),由于这一列/行的点只能由起点沿一条直线走过来,所以这些点的最佳路径总数都是

右上角的
接下来探讨求有限制的最佳路径问题。
例 1.2
求由
到 经过点 的最佳路径条数
这个问题可以分割为两个部分——从 我还能说什么呢,曼巴出去。
如果用组合数原理求解,也是需要分解成上述两个子问题,计算起来就是
Div 2. 缺刻网格
缺刻简直是学生物学的(确信)
我们接着来解决刚才提到的另一个网格路径计数问题:
例 2.1
求出从
点到 点的最佳路径总数
这个网格不再是一个完整的网格,而是缺了一角。放在生活中也很常见,道路维修之类的……接下来先探讨组合数解法(考纲内解法)。
首先,最短路径肯定是
如果这个网格是一个完整的网格,那么就是
大家可以发现,当网格被删去了某些点时,整个问题从组合数的角度考虑,就会增添巨大的思维量。在我看来,线性递推法能够在保证做到基本不出错的情况下,将这种题的推算时间压缩到一分钟内。在考场上就表现为有更多的时间死扣一道圆锥曲线的多选/填空/大题,并且线性递推的思维含量不高,能学会还是很赚的。
线性递推过程如下:

为什么缺刻部分的点的初始值是
本人亲测做题时间为 我甚至还没从四楼教室跑到食堂。
例 2.2
求出最佳路径条数
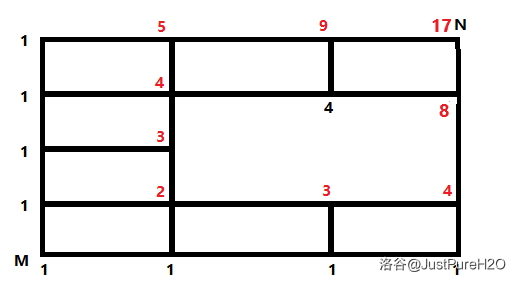
如果你学会了线性递推法,那么像这种中心缺刻网格你也能轻松切掉。递推过程如下图:
支持与分享
如果这篇文章对你有帮助,欢迎分享给更多人或赞助支持!
部分内容可能已过时




































































































