图论 二分图

二分图基础

二分图，又称二部图。顾名思义，在一个二分图中，所有的节点可以分成两部分（分别用黑白染色），并且满足相同颜色的点之间无边。如下图：

我们发现，集合 内部的点间都没有连边，每条边必定连接两个不同集合的点。二分图有一个性质，那就是不存在奇数环。因为每条边都连接了不同的集合，必须过偶数条边才能回到出发点所在的集合，因此长度为奇数的环是一定不可能出现在二分图里的。

染色法判定二分图

基于 ，对每次遍历到的点染色，并给它的邻接点染另一种颜色。如果某时刻出现矛盾（待染上的颜色与当前已有的颜色不同），则立马判定为非二分图，否则就是一个合法的二分图。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

bool dye(int u, int fa, int c) {
    color[u] = c;
    for (int i = h[u]; ~i; i = edges[i].ne) {
        int j = edges[i].to;
        if (j == fa) continue;
        if (color[j]) {
            if (color[j] == c) return false;  // 矛盾，不是二分图
        } else if (!dfs(j, u, 3 - c)) return false; // 在子树中出现矛盾，也不是二分图
    }
    return true;
}

bool check() {
    memset(color, 0, sizeof color);
    for (int i = 1; i <= n; i++) {
        if (!color[i]) {
            if (!dfs(i, -1, 1)) return false; // 出现矛盾，不是二分图
        }
    }
    return true;
}

二分图最大匹配

对于一个连接了若干条边的二分图，我们选出一些边，使得这些边没有公共点。满足如上条件且选出的边最多的方案称为这个二分图的最大匹配。

假如你是一名媒婆，你需要为若干对男女牵线搭桥（这是典型例子，并非本人玩梗整活）。已知他们的意向，如何选择才能让最多的男女成对（一夫一妻制、没有南通和钕通）。这就是一个裸的二分图最大匹配问题。

首先我们需要明确两个概念：

1. 交错路径：对于二分图中的某个匹配 ，有一条路径，使得这条路径上的边满足“不在 中”和“在 中”交替出现。则这个路径叫做交错路径，头尾边无限制。
2. 增广路径：如果交错路径上的边严格满足“不在 中”-“在 中”-“不在 中”-……-“在 中”-“不在 中”的顺序。则它是一个增广路径，即满足路径头尾的边都不在 中的交错路径。

匈牙利算法的核心就是在已经求解出的增广路径的基础上不断发现新的增广路径，增广路径上不相连接的边都可以组成一组匹配，因此只要增广路找的越长，就会找到比原先更大的匹配。

对于一张二分图，步骤如下：

1. 如果后边的节点所选的配对点与前边已选的点冲突，让前边的点寻找其他的配对
2. 在出现冲突的情况下，如果前边的点无论如何也找不到其他的配对，那么让后来的节点寻找其他的配对
3. 如果新来的节点均匹配不上，那么不做操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14

// 每次执行前需要清空st数组
bool hungary(int u) {
    for (int i = h[u]; ~i; i = edges[i].ne) {
        int j = edges[i].to;
        if (!st[j]) {
            st[j] = true; // 防止重复遍历
            if (!match[j] || hungary(match[j])) { // 当前这个女生还没配对成功或者先来的那个男生还有备胎
                match[j] = u; // 牵手成功
                return true;
            }
        }
    }
    return false; // 没招
}

点覆盖/路径覆盖/点独立

对于某个二分图，我们拿出若干个点组成一个点集，满足这张图所有边上至少有一个点在这个集合中。那么点数最少的这样的集合被称作原图的最小点覆盖集。根据 定理，二分图中最小点覆盖集的大小等于最大匹配数，即这个最小点集中的点数等于最大匹配的边数。

相对的，我们选出若干点组成另一个点集，让点集里任意两点在原图中均不相连，满足它的最大点集叫做最大点独立集；与之相对，选出一些点，使得任意两点间都有边，满足它的最大点集叫做原图的最大团。假设原图为 ，把 中原有的边删去、并把没有边连接的两点连接上，得到它的补图 ，那么 的最大点独立集的大小等于 最大团的大小。

对于一张 ，用若干互不相交（没有公共端点）的路径把所有点覆盖，其中选取路径数最少的那个方案，叫做这个 的最小路径覆盖。如果使用的路径允许相交，则叫做最小路径重复点覆盖。

在二分图中，有如下非常好的性质：

1. 最小点覆盖集的大小=最大匹配数—— 定理
2. 总点数-最小点覆盖集的大小=总点数-最大匹配数=最大点独立集的大小
3. 最小路径覆盖数=顶点数-最大匹配数

对于第二点，感性理解一下：我们要选出若干点丢弃，使得剩余的点无论如何也不互通。考虑到最小点覆盖的定义，我们把属于最小点覆盖集的所有点从图中去掉，此时图中所有边均只有一个端点，无法经过边到达其他点。

对于第三点。在任意 中，把同一个点拆分成两个点，分居两侧，因此可以组成一个二分图。原图中的边 ，在新图里就可以映射成 。因此，对于原图中的每一条路径，在这个二分图的右部都可以找到对应的终点（每一条路径都有终点，终点出度为 ，在二分图中匹配失败）。右部失配点对应一个左部的非匹配点，转化成求左部非匹配点最少，从而变成求左部匹配点最多，最后变成求最大匹配数。

如何求解最小路径重复点覆盖数呢？我们想办法把它转化成简单的问题——比如当前有两条边 和 相交在 点，那么我们可以考虑让其中一条边的两个端点不经过 直接相连，一来二去，整个问题会变成求解新图的最小路径覆盖数。根据如上原理，把所有能够间接到达的点直接连上，也就是说先求解原图的传递闭包，最后在新图上解最小路径覆盖数。

典例

洛谷 P1525 [NOIP2010 提高组] 关押罪犯

题目地址：P1525

题目难度：普及+/提高

题目来源：NOIp 提高组  2010

NOIP2010 提高组 T3

S 城现有两座监狱，一共关押着 名罪犯，编号分别为 。他们之间的关系自然也极不和谐。很多罪犯之间甚至积怨已久，如果客观条件具备则随时可能爆发冲突。我们用“怨气值”（一个正整数值）来表示某两名罪犯之间的仇恨程度，怨气值越大，则这两名罪犯之间的积怨越多。如果两名怨气值为 的罪犯被关押在同一监狱，他们俩之间会发生摩擦，并造成影响力为 的冲突事件。

每年年末，警察局会将本年内监狱中的所有冲突事件按影响力从大到小排成一个列表，然后上报到 S 城 Z 市长那里。公务繁忙的 Z 市长只会去看列表中的第一个事件的影响力，如果影响很坏，他就会考虑撤换警察局长。

在详细考察了 名罪犯间的矛盾关系后，警察局长觉得压力巨大。他准备将罪犯们在两座监狱内重新分配，以求产生的冲突事件影响力都较小，从而保住自己的乌纱帽。假设只要处于同一监狱内的某两个罪犯间有仇恨，那么他们一定会在每年的某个时候发生摩擦。

那么，应如何分配罪犯，才能使 Z 市长看到的那个冲突事件的影响力最小？这个最小值是多少？

输入格式：

每行中两个数之间用一个空格隔开。第一行为两个正整数 ，分别表示罪犯的数目以及存在仇恨的罪犯对数。接下来的 行每行为三个正整数 ，表示 号和 号罪犯之间存在仇恨，其怨气值为 。数据保证 ，且每对罪犯组合只出现一次。

输出格式：

共一行，为 Z 市长看到的那个冲突事件的影响力。如果本年内监狱中未发生任何冲突事件，请输出 0。

数据范围

对于 的数据有 。

最大值最小，考虑二分。设当前二分到的最大冲突值是 ，我们判断这个答案是否可行。就需要把所有冲突值小于等于它的某对罪犯放进同一个监狱，反之放进不同的监狱。这个方案成立当且仅当整个图能够构成一张二分图，因为只有如此，才能保证先前假设的所有罪犯关系成立，且不存在比当前二分到的更大的冲突。

因此在二分到每个答案时，对建立的图进行一次染色法判定。如果当前是一个二分图，则把右边界缩减，反之收缩左边界。

AcWing 372 棋盘覆盖

题目地址：AcWing 372

题目难度：中等

给定一个 行 列的棋盘，已知某些格子禁止放置。

求最多能往棋盘上放多少块的长度为 、宽度为 的骨牌，骨牌的边界与格线重合（骨牌占用两个格子），并且任意两张骨牌都不重叠。

输入格式：

第一行包含两个整数 和 ，其中 为禁止放置的格子的数量。

接下来 行每行包含两个整数 和 ，表示位于第 行第 列的格子禁止放置，行列数从 开始。

输出格式：

输出一个整数，表示结果。

数据范围：

棋盘问题一般考虑两种：状态压缩DP和二分图，但是状压DP的时间复杂度是 ，这道题不行。因此考虑后者。

在抛除了被禁用格子的情况下，尝试把能放的两个相邻格子当作两个点连边。不相邻的格子/禁止放置的格子不连边，最后发现整张图就是一个二分图。那么我们需要解决的就是——选择没有重复端点（不重叠）的若干条边，使得利用率最高，因此做二分图的最大匹配。

对于棋盘问题， 二分图在建图时有一个小技巧：就是把棋盘上色，变成一个国际象棋的棋盘（横纵黑白交替）。我们可以发现，对于任何一个可放置骨牌的位置，两个格子的颜色是不相同的。形式化讲，必定有一种颜色的格子全部满足横纵坐标之和为奇数。因此我们只需让横纵坐标之和为偶数的格式向和为奇数的格子连边即可。于是枚举所有和为奇数的点（二分图左部的所有点）做匈牙利算法。

UVA 1194 Machine Schedule

题目地址：UVA 1194

题目难度：提高+/省选-

有两台机器 分别有 种模式。

现在有 个任务。对于每个任务 ，给定两个整数 和 ，表示如果该任务在 上执行，需要设置模式为 ；如果该任务在 上执行，需要设置模式为 。

每台机器第一次开机默认处在0模式，且第一次开机不需要消耗时间。任务可以以任意顺序被执行，但每台机器转换一次模式就要重启一次。求怎样分配任务并合理安排顺序，能使机器重启次数最少。

输入格式：

多组测试数据。对于每组数据，输入第一行为三个整数 ，含义见上。

接下来 行，每行三个整数 。分别代表任务编号， 和 。

当末尾出现单独的 时，读入结束

输出格式：

对于每组测试数据，输出一行一个整数，代表最少的重启次数

数据范围：

，，，。

原题 PDF

考虑把每一个 设置成一个点，从 向 连边，代表整个任务 ，只要其中有一方调节了模式并执行这个任务，则可以看作整个任务完成了。发现最终得到的图是一张二分图，左部为 ，右部为 。问题就转化成了——找出若干 ，使得这些选出的点能够覆盖到所有的任务（边）。因此是一道求解二分图最小点覆盖的题目，根据 定理，我们只需要解出这个图的最大匹配数即可。

洛谷 P3355 骑士共存问题

题目地址：P3355

题目难度：省选/NOI-

题目来源：网络流与线性规划 24 题

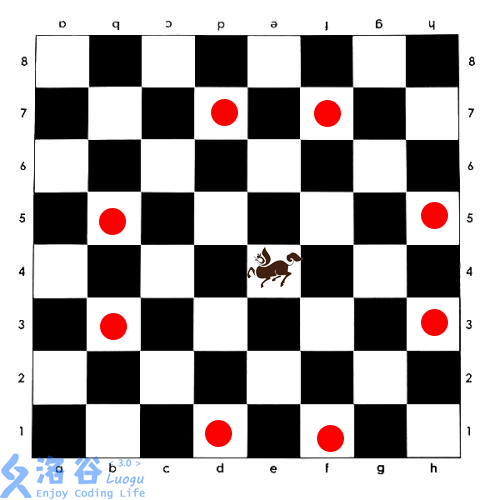
在一个 个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入。

对于给定的 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击。

输入格式：

第一行有 个正整数 和 ，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 个正整数，表示障碍的方格坐标。

输出格式：

将计算出的共存骑士数输出。

数据范围：

对于全部的测试点，保证 ，。

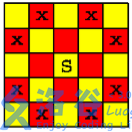
同样使用棋盘技巧，题图已经非常直观的展现了这一技巧。我们发现所有黄色的格子都可以向周围符合要求的红色格子连边，红黄两色组成二分图。根据题意，我们要放尽量多的点，使得它们伸展出去的边互不相干（所有点互不相通）。因此这是一道求解二分图最大独立集的问题，转化成“总点数减障碍点数减最大匹配数”的求解。同样只枚举单色格子来求解（二分图的某一部）。

双倍经验：P4304 [TJOI2013] 攻击装置

洛谷 P5030 长脖子鹿放置

题目地址：P5030

题目难度：省选/NOI-

众周所知，在西洋棋中，我们有城堡、骑士、皇后、主教和长脖子鹿。

如图所示，西洋棋的“长脖子鹿”，类似于中国象棋的马，但按照“目”字攻击，且没有中国象棋“别马腿”的规则。（因为长脖子鹿没有马腿）

给定一个,的棋盘，有一些格子禁止放棋子。问棋盘上最多能放多少个不能互相攻击的长脖子鹿。

输入格式：

输入的第一行为两个正整数，，。其中表示禁止放置长脖子鹿的格子数。

第~第行每一行为两个整数,表示禁止放置的格子。

不保证禁止放置的格子互不相同。

输出格式：

一行一个正整数，表示最多能放置的长脖子鹿个数。

数据范围/提示：

重要提示：请务必思考对图的遍历顺序对运行速度的影响

对于的数据，

这道题和上面那一道很像，但不是双倍经验，关键就在于该题的移动方式上。由图可知，此时中心的白色方格需要向周围的同色方格连边，按照常规方法是建不出二分图的（同颜色连向同颜色），因此考虑更换建图方式（棋盘染色方式）。

好在，我们发现中心棋子和红点所在行数的奇偶性是不同的，此时可以转化成奇数行向偶数行上的合法点连边。把奇偶性不同的行染成黑白二色，发现就是一个二分图了。因此我们只需要枚举所有奇数行的所有列，套用上一题求解最大点独立集的公式就可解决这道题。

AcWing 379 捉迷藏

题目地址：AcWing 379

题目难度：中等

Vani 和 cl2 在一片树林里捉迷藏。

这片树林里有 座房子， 条有向道路，组成了一张有向无环图。

树林里的树非常茂密，足以遮挡视线，但是沿着道路望去，却是视野开阔。

如果从房子 沿着路走下去能够到达 ，那么在 和 里的人是能够相互望见的。

现在 cl2 要在这 座房子里选择若干座作为藏身点，同时 Vani 也专挑 cl2 作为藏身点的房子进去寻找，为了避免被 Vani 看见，cl2 要求所选的这几个藏身点的任意两个之间都没有路径相连。

为了让 Vani 更难找到自己，cl2 想知道最多能选出多少个藏身点。

输入格式：

输入数据的第一行是两个整数 和 。

接下来 行，每行两个整数 ，表示一条从 到 的有向道路。

输出格式：

输出一个整数，表示最多能选取的藏身点个数。

数据范围：

。

乍一看，这不是最大点独立集的问题吗？然而并不是，它只存在于无向图中。此处给出的是一个 ，对于 ，有一个概念叫最小路径点覆盖。它的定义是：选出最少的不相交的边，使得选出的这些边能够覆盖到所有的点。如果我们选择了过多的点，那么会出现互通的点，与题意矛盾。再考虑到题目给出“相互望见”的关系，这道题会边成一个最小路径重复点的求解，因此求传递闭包即可。

双倍经验：UVA 1184 - Air Raid（最小路径点覆盖数）

洛谷 P2764 最小路径覆盖问题

题目地址：P2764

题目难度：省选/NOI-

题目来源：网络流与线性规划 24 题  Special Judge

给定有向图 。设 是 的一个简单路（顶点不相交）的集合。如果 中每个定点恰好在 的一条路上，则称 是 的一个路径覆盖。 中路径可以从 的任何一个定点开始，长度也是任意的，特别地，可以为 。 的最小路径覆盖是 所含路径条数最少的路径覆盖。设计一个有效算法求一个 DAG（有向无环图） 的最小路径覆盖。

输入格式：

第一行有两个正整数 和 。 是给定 DAG（有向无环图） 的顶点数， 是 的边数。接下来的 行，每行有两个正整数 和 表示一条有向边 。

输出格式：

从第一行开始，每行输出一条路径。文件的最后一行是最少路径数。

对于 的数据，，。

这道题在求解最小路径覆盖数的基础上额外设置了一个输出合法路径的要求，考虑到 match 数组的含义——配对的点。又因为配对的点在同一条路径上，所以可以从每个点开始向前递归查找路径，只要还能配对，那么加入当前路径，否则新开一个路径存储其他的路径。

需要注意的是，对原 进行重映射时我们把右部点的编号统一设置成了左部点编号加 的形式，因此在操作时需要注意转换。一般情况的递归寻路代码如下：

1
2
3
4
5
6
7
8
9

void getPath(int u) {
    path[tot].push_back(u); // 当前点加入路径
    st[u] = true;           // 标记已访问，后期不再单独作为路径起点进行递归
    if (!pre[u].second) {   // 不存在前驱，代表是路径的端点
        tot++;              // 开新路径
        return;
    }
    getPath(pre[u].second); // 递归它的前驱
}

洛谷 P6062 [USACO05JAN] Muddy Fields G

题目地址：P6062

题目难度：省选/NOI-

题目来源：USACO  2005

大雨侵袭了奶牛们的牧场。

牧场是一个 的矩形，其中 。大雨将没有长草的土地弄得泥泞不堪，可是小心的奶牛们不想在吃草的时候弄脏她们的蹄子。为了防止她们的蹄子被弄脏，约翰决定在泥泞的牧场里放置一些木板。每一块木板的宽度为 个单位，长度任意，每一个板必须放置在平行于牧场的泥地里。

约翰想使用最少的木板覆盖所有的泥地．一个木板可以重叠在另一个木板上，但是不能放在草地上。

输入格式：

第一行两个整数 。

接下来 行，每行 个字符，描述牧场，其中 * 为泥地，. 为草地。

输出格式：

输出一个整数，最少需要多少木板。

对于每个能够放置木板的格子，显然一次性放更长的木板会更优，对于任何一个泥方格，它都可能位于一个横向的木板或是一个纵向的木板上。这启发我们先处理出每个泥方块所在的最长的横向/纵向连通块，然后把所有横向连通块和纵向连通块分开、组成二分图的左右部，接着根据每个泥方块所在的位置，为相关的横纵连通块表示的点连边。目标是将所有泥地覆盖起来，因此这道题就只需要我们求出这个二分图的最小点覆盖。

CF 1404E Bricks

题目地址：CF 1404E

题目难度：省选/NOI-

你有一个 （）的格子纸，格子要么涂黑（#）要么涂白（.）。你需要用若干个长为一，宽为任意正整数或者宽为一，长为任意正整数的长方形去覆盖所有黑色格子，要求不能盖到白色格子上，不能盖到其他长方形上，不能盖出格子纸的边界，求最少用多少个长方形。

数据保证至少有一个黑色格子。

输入格式：

输入第一行为两个整数 。

接下来 行描述这个格子纸，每行包含一个长度为 的字符串，包含“#”和“.”两种字符型，分别代表对应位置上有一个黑色格子和一个白色格子。

数据保证至少存在一个黑色格子。

输出格式：

输出一行一个整数，代表所需最少的长方形数

这道题其实和上边的题十分相似，唯一不同的一点是——这道题不允许木板重叠。此时需要更换建图方式，把方格看作点，点之间有边，代表原方格纸上两个方格有公共边。考虑到木板重叠只会出现在十字交叉的位置，因此着重研究此类方格。如果我们假设边上还有若干黑白点，那么当选择了某条边上的点 （覆盖一个长方形）后，另一个方向的边上的点 就不能被选择（含义为覆盖当前点）。因此给 连边。最终，会得到一个二分图，并且我们希望在二分图上每个点都不能互相到达的情况下覆盖到每个原图点，于是在新图跑最大独立集。

更为详细的内容见：我的题解

CF 1728F Fishermen

题目地址：CF 1728F

题目难度：NOI/NOI+/CTSC

没想到有生之年居然还能用得上黑题的tag……

给你一个长度为 的序列 ，你可以将 中的数重新排列，并根据重排后的序列 生成序列 ，生成方法如下：

• 。
• ， 是满足 且 的最小正整数。

求所以可能生成的序列 中 的最小值。

输入格式：

输入第一行为一个整数 ，代表 中的元素个数。

第二行有 个整数 ，满足 。

输出格式：

一行一个整数，代表最小的 。

考虑到给出的两个生成方法对我们的构造没有影响，我们完全可以在构造后对 进行重排得到合法解（题目还没要求输出方案）。发现只要满足 ，且 互不相同（小于号）即可。根据整除的性质，设倍率 ，显然当 过大时，生成的倍数就不优了，不满足“ 的最小正整数”这一性质。于是设置 。因为倍数可能很大，所以考虑离散化。

读题可以发现，题目要求让每一个 都能配对一个 ，考虑二分图匹配。把有倍数关系的 和预处理的数字连上边。对于题目中的 最小，运用贪心思想，我们把预处理的倍数按照升序排序即可解决。

更为详细的内容见：我的题解

所有代码在此