强连通分量与 Tarjan 缩点

连通分量与缩点

在说之前，先涉及最基本的概念：连通分量。如果一张有向图中，任意两个节点都能互相到达，则称它是一个连通分量，特殊地，一个点也算一个连通分量。强连通分量Strongly Connected Component，简称（~~四川菜~~），是原图的极大连通分量。这里的“极大”是一个文艺复兴时期提出的概念——若一个事物，没有比它更大的事物存在，就称这个事物是极大的/最大的（例如：导数的极大值）。

缩点，指在求出图上所有后把这些分量用一个点去代替。这样操作得到的新图是一张有向无环图Directed Acyclic Graph，简称（大哥）。它可以做拓扑排序，在这样的图上做最短路，时间复杂度是的，优于的或者的。

求解最常用的算法由发明（~~整个世界就是一个巨大的~~ ），在图上做一遍深度优先搜索，并维护相关信息；以及不那么常用但是非常直观好理解的算法，在正反图上分别进行一次深搜从而得到强连通分量。

算法流程

生成树基础

假如当前遍历了绿色的边及其相连的节点。我们可以把图上的边分为四类：

树枝边：正常的树内边，标记为黑色有向。
前向边：指向前方的边，也就是从上向下指的边。可以发现树枝边就是一类特殊的前向边。标记为蓝色有向
后向边：指向后方的边，与前向边相对。标记为橙色有向。
横叉边：指向一个已经访问过的节点，且这个节点不是它的父节点。标记为紫色有向。

如果某个节点是某个中被访问到的第一个节点，那么强连通分量中其余节点在这个节点的子树上。

算法思路

首先为每个节点维护两个变量 dfn 和 low，这两者都是维护节点信息的“时间戳”。前者用来记录深搜时该点是第几个被访问到的；后者定义为这个点在栈中能够回溯到的最早加入的节点 dfn。对于某个强连通分量，我们会发现这个分量中的所有点的 low 值均是相同的，如下图：

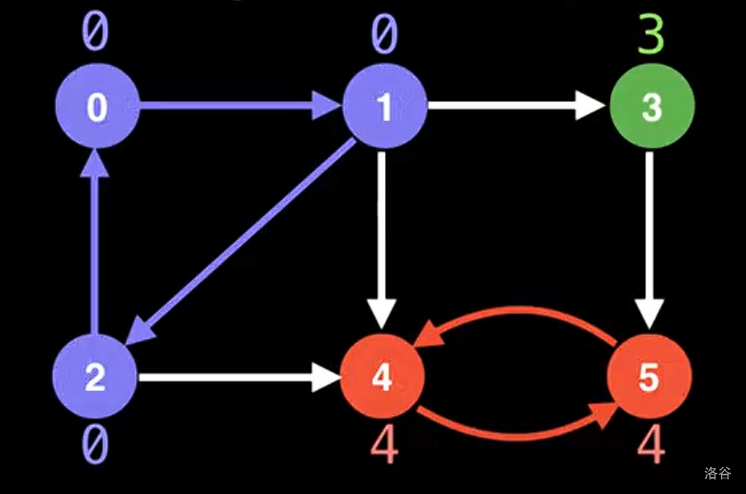
其中点内的序号是 dfn 值，点外侧的数字是 low 值。此时再维护一个栈，栈中存放已经深搜遍历到且还没计算出归属于哪个强连通分量的节点。

这启发我们做深搜，先把当前点的 dfn 值标记出来，并枚举相连的点（不是父节点），那么对于节点的 low 值，分三种情况讨论：

如果枚举到一条树枝边，则 low[x] = min(low[x], low[y])。这基于一个事实—— 能到达的节点，也能。
如果这条边不是树枝边，但是在栈中，则 low[x] = min(low[x], dfn[y])。根据 low 的定义而来（有向图中使用 low[x] = min(low[x], low[y]) 也是正确的）。
如果这条边不是树枝边，且不在栈中，则不作操作。因为这意味着所属的已被全部处理完且弹出栈了，二者因此不同属于一个强连通分量中。

如果当前的点满足 dfn[u] = low[u]，等价于它能回溯到的最早的点是自己，代表这是一个的起始节点。因此我们不断弹出栈顶，加入到新的中，直到弹出并把它加入强连通分量后为止，此时可以借机维护一下强连通分量的相关变量。

基本模板：

void tarjan(int u) {
    stack<int> stk;
    dfn[u] = low[u] = ++dfs_cnt;
    stk.push(u);
    in_stk[u] = true;

    for (int i = h[u]; ~i; i = edges[i].ne) {
        int j = edges[i].to;
        if (!dfn[j]) {
            tarjan(j);
            low[u] = min(low[u], low[j]);
        } else if (in_stk[j]) {
            low[u] = min(low[u], dfn[j]);
        }
    }
    if (dfn[u] == low[u]) {
        scc_cnt++;
        do {
            int t = stk.top();
            stk.pop();
            scc_id[t] = scc_cnt;
        } while (stk.top() != u);
    }
}

缩点流程

所谓缩点，说白了就是把解出来的强连通分量当作一个单点，建出一个新图，此时这个新图是一个。正常来说首先就需要做算法分离所有强连通分量，然后再根据不同强连通分量内点的连接关系来连之间的边。注意，有可能出现多对分属不同点、缩点后反复在同一对强连通分量之间连边的情况，大部分时候无需在意，但是在特殊情况下可能需要对这些边判重。

for (int i = 0; i <= n; i++) {
    for (int j = h[i]; ~j; j = edges[j].ne) {
        int k = edges[j].to;
        int a = scc_id[i], b = scc_id[k];
        if (a != b) add(hs, a, b, edges[j].w);
    }
}

典例演练

为了方便，我们把缩点后入度为的点称作“起点”、出度为的点称为“终点”。

洛谷 P2341 [USACO03FALL/HAOI2006] 受欢迎的牛 G

题目地址：P2341

题目难度：普及+/提高

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果喜欢，喜欢，那么也喜欢。牛栏里共有头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。

输入格式：

第一行：两个用空格分开的整数：和。

接下来行：每行两个用空格分开的整数：和，表示喜欢。

输出格式：

一行单独一个整数，表示明星奶牛的数量。

数据范围：

对于的数据，，。

把所有的“喜欢关系”画成一个有向图：

强连通分量用绿色矩形框出，把绿色框当作一个点。已知框内的点两两互通，只要某个框内的某个点和另一个点连通，那么整个框的点都和这个点相通。因此连通关系就可以传递下来，于是我们需要解决的就是其他方框之间的连通性。

把绿色框看成单点（缩点）后，如果所有边最终汇聚到一个点上，那么这个中的所有点都和其他所有点相连，就是符合题目要求的“明星~~ヒマリ~~”。因此我们只需统计出度为的即可：如果仅有一个这样的强连通分量，那么答案就是这个强连通分量里的总点数；若出现一个以上这样的，则答案为（毕竟连两个终点都不互连通）。

代码在此

洛谷 P2746 [USACO5.3] 校园网 Network of Schools

题目地址：P2746

题目难度：提高+/省选-

一些学校连入一个电脑网络。那些学校已订立了协议：每个学校都会给其它的一些学校分发软件（称作“接受学校”）。注意即使在学校的分发列表中，也不一定在学校的列表中。

你要写一个程序计算，根据协议，为了让网络中所有的学校都用上新软件，必须接受新软件副本的最少学校数目（子任务 A）。更进一步，我们想要确定通过给任意一个学校发送新软件，这个软件就会分发到网络中的所有学校。为了完成这个任务，我们可能必须扩展接收学校列表，使其加入新成员。计算最少需要增加几个扩展，使得不论我们给哪个学校发送新软件，它都会到达其余所有的学校（子任务 B）。一个扩展就是在一个学校的接收学校列表中引入一个新成员。

输入格式：

输入文件的第一行包括一个正整数，表示网络中的学校数目。学校用前个正整数标识。

接下来行中每行都表示一个接收学校列表（分发列表），第行包括学校的接收学校的标识符。每个列表用结束，空列表只用一个表示。

输出格式：

你的程序应该在输出文件中输出两行。

第一行应该包括一个正整数，表示子任务 A 的解。

第二行应该包括一个非负整数，表示子任务 B 的解。

数据范围：

。

我们同样处理出点之间的关系，图中一定有个起点与个终点。对于子任务，当这个软件在起点开始投放时，才能到达更多的学校，要想到达所有的学校，就需要在缩点后的所有起点都放上这个软件，因此答案是；对于子任务，我们的答案是，但如果整张图是一整个，就不需要再连任何边，答案就是。

对于子任务的感性理解：每个点都需要互相连通，首先就不能存在入度/出度为的节点，因此最节省边的方式就是让起点和终点连边。一一对应地连，数量更少的那种点就会率先被连完，剩下的就是数量更多的那种点，再随便连几条边把剩余节点消耗完。最终答案就是。当然若全图是一个则无需理会。

代码在此

四倍经验：P2812 校园网络加强版、P2835 刻录光盘、P1262 间谍网络、P2002 消息扩散

洛谷 P2272 [ZJOI2007] 最大半连通子图

题目地址：P2272

题目难度：提高+/省选-

题目来源：浙江 2007 各省省选

一个有向图称为半连通的 (Semi-Connected)，如果满足：，满足或，即对于图中任意两点，存在一条到的有向路径或者从到的有向路径。

若满足，是中所有跟有关的边，则称是的一个导出子图。若是的导出子图，且半连通，则称为的半连通子图。若是所有半连通子图中包含节点数最多的，则称是的最大半连通子图。

给定一个有向图，请求出的最大半连通子图拥有的节点数，以及不同的最大半连通子图的数目。由于可能比较大，仅要求输出对的余数。

输入格式：

第一行包含两个整数。分别表示图的点数与边数，的意义如上文所述。

接下来行，每行两个正整数，表示一条有向边。图中的每个点将编号为，保证输入中同一个不会出现两次。

输出格式：

应包含两行，第一行包含一个整数，第二行包含整数。

数据范围：

对于的数据，，，。

阅读题面可以发现，其实本身就是一种特殊的半连通图，因此我们尽量多选图中的。这就需要我们先缩点，缩点后再找最大的半连通子图。本着多选强连通分量的原则，对于缩点后的，我们选择最长的一条链（事实上，要求路径上所有强连通分量所包含点的总数最大）即可。

对于方案数，考虑 DP。做最长链的时候，如果发现下一个状态能够被更新，则更新总点数、同时把上一个点的方案计数覆盖过去；如果转移时发现路径长度相等，则把上一个点的方案数累加过去。

这时，我们需要对缩点后的图去重边，因为在 DP 转移时需要枚举出边，重边会造成点数的重复计算。因此使用哈希表进行去重。

代码在此

AcWing 368 银河

题目地址：AcWing 368

题目难度：中等

银河中的恒星浩如烟海，但是我们只关注那些最亮的恒星。

我们用一个正整数来表示恒星的亮度，数值越大则恒星就越亮，恒星的亮度最暗是。

现在对于颗我们关注的恒星，有对亮度之间的相对关系已经判明。

你的任务就是求出这颗恒星的亮度值总和至少有多大。

输入格式：

第一行给出两个整数和。

之后行，每行三个整数，表示一对恒星之间的亮度关系。恒星的编号从开始。

如果，说明和亮度相等。如果，说明的亮度小于的亮度。如果，说明的亮度不小于的亮度。如果，说明的亮度大于的亮度。如果，说明的亮度不大于的亮度。

输出格式：

输出一个整数表示结果。

若无解，则输出。

数据范围：