抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

生成树算法

oi算法

发布于：2024年6月14日

字数：4.5k 字

时长：17 分钟

生成树基础

生成树，在 OI 中最多的考法有两种——最小生成树和次小生成树。最小生成树（Minimum Spanning Tree，MST）是最常见的问题，它是原图边权之和最小的生成树（不一定唯一）；而次小生成树，分为严格次小生成树和非严格次小生成树，前者要求次小生成树的权值和严格小于最小生成树的权值和，后者则无此要求，即允许“大于等于”情况的出现。实际考察严格次小生成树较多。

生成树基础算法

Prim （稠密图）

算法的思想类似于 算法，都是使用一个点去松弛并更新新的相连的节点。对于当前到达的节点，遍历它的相邻边，如果选中当前边后的权值小于数组中存储的 值时，就更新并将连接到的点加入队列。与 相同， 也可以使用堆优化来提升效率。

这个算法（加入堆优化）的时间复杂度是 的。不过我一般不用这个算法，原因是 的局限性较高，并且尽管是稠密图，它的运行效率也不一定比 算法高、后者的理解和实现门槛更低，所以在最小生成树问题中 算法永远都是首选。

Kruskal （墙裂推荐）

算法基于贪心思想，它的想法非常直白——把已有的边从小到大排序，按边权升序挑出边，如果边两头的节点已在生成树中，则跳过；反之若两点不都在生成树中，就添加上这条边。从而保证了最终生成树的边权之和最小。

当然，要想维护节点的从属关系。最适合最高效的数据结构当然就是并查集了，它能够在几近于常数的时间复杂度内快速求出两个节点的从属关系。我们依次取出边，判断这个边相连的两个点是否已经全部位于生成树内，若不都在生成树内，那么加入这个边，累加权值和边的数量。当选中的边数到达 时即可退出循环了。

具体实现如下（对应题目P3366）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>
#define N 200010
using namespace std;

int p[N], n, m;

struct Edge {
	int a, b, w;

	bool operator< (const Edge &r) {
		return w < r.w;
	}
} edges[N];

int find(int x) {
	if (p[x] != x) return find(p[x]);
	return p[x];
} 

bool query(int a, int b) {
	return find(a) == find(b);
}

void merge(int x, int y) {
	p[find(x)] = y;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
  
	cin>>n>>m;
	for (int i = 1; i <= m; i++) {
		cin>>edges[i].a>>edges[i].b>>edges[i].w;
	}
	sort(edges, edges + m);
	for (int i = 1; i <= n; i++) p[i] = i;

	int res = 0, cnt = 0;
	for (int i = 1; i <= m; i++) {
		int a = edges[i].a;
		int b = edges[i].b;
		int w = edges[i].w;
		if (!query(a, b)) {
			merge(a, b);
			res += w;
			cnt++;
		}
	} 
	if (cnt < n - 1) cout<<"orz"<<endl;
	else cout<<res<<endl;
	return 0; 
}

最小生成树最长边权求解

洛谷 P2330 繁忙的都市

题目地址：P2330

题目难度：普及/提高-

题目来源：四川  2005

城市 C 是一个非常繁忙的大都市，城市中的道路十分的拥挤，于是市长决定对其中的道路进行改造。城市 C 的道路是这样分布的：城市中有 个交叉路口，有些交叉路口之间有道路相连，两个交叉路口之间最多有一条道路相连接。这些道路是双向的，且把所有的交叉路口直接或间接的连接起来了。每条道路都有一个分值，分值越小表示这个道路越繁忙，越需要进行改造。但是市政府的资金有限，市长希望进行改造的道路越少越好，于是他提出下面的要求：

  1. 改造的那些道路能够把所有的交叉路口直接或间接的连通起来。
  2. 在满足要求 1 的情况下，改造的道路尽量少。
  3. 在满足要求 1、2 的情况下，改造的那些道路中分值最大的道路分值尽量小。

任务：作为市规划局的你，应当作出最佳的决策，选择哪些道路应当被修建。

输入格式：

第一行有两个整数 表示城市有 个交叉路口， 条道路。

接下来 行是对每条道路的描述， 表示交叉路口 和 之间有道路相连，分值为 。

输出格式：

两个整数 ，表示你选出了几条道路，分值最大的那条道路的分值是多少。

数据范围：

对于全部数据，满足 ，，。

这道题相当于让我们求出最小生成树的边数和选择的最大边权。考虑到最小生成树求解的顺序是边权升序，那么当最小生成树的最后一条边被选定时，此时的边权一定是答案所求的最大边权。在 选边时更新即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 部分省略
int main() {
    // 部分省略...
    int ans = INFINITY;
    for (int i = 1; i <= m; i++) {
        int u = edges[i].u;
        int v = edges[i].v;
        int w = edges[i].w;
        if (!related(u, v)) {
            merge(u, v);
            ans = w;
        }
    }
    cout << n - 1 << ' ' << ans << endl;
    return 0;
}

双倍经验：P1547

最小生成树综合

AcWing 1146 新的开始

题目地址：AcWing 1146

题目难度：中等

发展采矿业当然首先得有矿井，小 FF 花了上次探险获得的千分之一的财富请人在岛上挖了 口矿井，但他似乎忘记了考虑矿井供电问题。

为了保证电力的供应，小 FF 想到了两种办法：

  1. 在矿井 上建立一个发电站，费用为 （发电站的输出功率可以供给任意多个矿井）。
  2. 将这口矿井 与另外的已经有电力供应的矿井 之间建立电网，费用为 。

小 FF 希望你帮他想出一个保证所有矿井电力供应的最小花费方案。

输入格式：

第一行包含一个整数 ，表示矿井总数。

接下来 行，每行一个整数，第 个数 表示在第 口矿井上建立发电站的费用。

接下来为一个 的矩阵 ，其中 表示在第 口矿井和第 口矿井之间建立电网的费用。

数据保证 ，且 。

输出格式：

输出一个整数，表示让所有矿井获得充足电能的最小花费。

数据范围

这道题是最小生成树与虚拟源点的综合，所谓虚拟源点，就是假想一个不存在的点，当作统一的起点，从而避免了对起点进行无意义枚举、重复计算的困境。

考虑创建一个“零号点”，当作一个发电站，那么这个点向其他点连边的意义就是“在当前点建立一个发电站”，显而易见的，边权应是 。对于操作2，就是单纯的生成树两点连边。因此我们预先处理输入的邻接矩阵，然后枚举并创建无向边 ，将边权设为 。值得注意的是， 算法读入的是无向边，但是它并不需要向前向星那样建两次边，只需要建一次，所以读入邻接矩阵的一半就好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        // 读入一半的邻接矩阵
        int x;
        cin >> x;
        if (i >= j) continue;
        edges[++cnt].u = i;
        edges[cnt].v = j;
        edges[cnt].w = x;
    }
}
for (int i = 1; i <= n; i++) {
    // 超级源点的建边
    edges[++cnt].u = 0;
    edges[cnt].v = i;
    edges[cnt].w = vi[i];
}
sort(edges + 1, edges + 1 + cnt, cmp);
int ans = 0, ed = 0;
for (int i = 1; i <= cnt; i++) {
    int u = edges[i].u;
    int v = edges[i].v;
    int w = edges[i].w;
    if (!related(u, v)) {
        merge(u, v);
        ans += w;
        ed++;
        if (ed == n) break;
    }
}

变量 ans 的值是最终答案。

洛谷 P4047 [JSOI2010] 部落划分

题目地址：P4047

题目难度：普及+/提高

题目来源：江苏  2010

聪聪研究发现，荒岛野人总是过着群居的生活，但是，并不是整个荒岛上的所有野人都属于同一个部落，野人们总是拉帮结派形成属于自己的部落，不同的部落之间则经常发生争斗。只是，这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。

不过好消息是，聪聪得到了一份荒岛的地图。地图上标注了 个野人居住的地点（可以看作是平面上的坐标）。我们知道，同一个部落的野人总是生活在附近。我们把两个部落的距离，定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了 个部落！这真是个好消息。聪聪希望从这些信息里挖掘出所有部落的详细信息。他正在尝试这样一种算法：

对于任意一种部落划分的方法，都能够求出两个部落之间的距离，聪聪希望求出一种部落划分的方法，使靠得最近的两个部落尽可能远离。

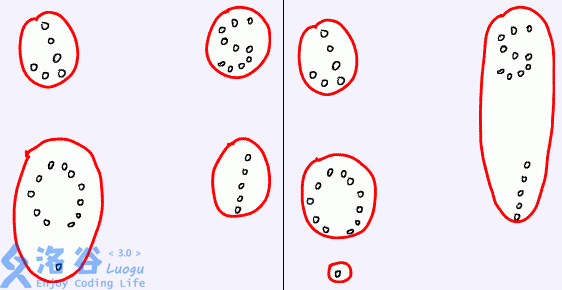
例如，下面的左图表示了一个好的划分，而右图则不是。请你编程帮助聪聪解决这个难题。

输入格式：

输入文件第一行包含两个整数 和 ，分别代表了野人居住点的数量和部落的数量。

接下来 行，每行包含两个整数 ，，描述了一个居住点的坐标。

输出格式：

输出一行一个实数，为最优划分时，最近的两个部落的距离，精确到小数点后两位。

数据范围：

对于 的数据，保证 ，。

这道题关联到并查集维护连通块个数的功能。在初始时，每个点都单独地作为一个连通块，整张图上就有 个连通块。那么每次建边就相当于将两个不同的连通块合并到一起，此时将存储连通块个数的变量减去一，当变量的值第一次小于等于 时，便可将下一个边的值输出。这个操作的原理依旧是最小生成树边权的升序排序，因此输出连通块总数小于等于 后取出的第一个边权即可。这里的边权就是两个村庄的欧几里得距离。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
double ans = 0;
int c = n; // 连通块的个数，初始时为n
for (int i = 1; i <= cnt; i++) {
    int u = edges[i].u;
    int v = edges[i].v;
    double w = edges[i].w;
    bool flag = false;
    if (c <= k) flag = true; // 第一次小于等于k，记录一下
    if (!related(u, v)) {
        merge(u, v);
        c--; // 成功连边，合并了两个连通块，总数减一
        if (flag) {
            ans = w; // 连通块总数小于等于k后第一个边权即为答案
            break;
        }
    }
}

双倍经验：P1991

AcWing 346 走廊泼水节

题目地址：AcWing 346

题目难度：中等

给定一棵 个节点的树，要求增加若干条边，把这棵树扩充为完全图，并满足图的唯一最小生成树仍然是这棵树。

求增加的边的权值总和最小是多少。

注意： 树中的所有边权均为整数，且新加的所有边权也必须为整数。

输入格式：

第一行包含整数 ，表示共有 组测试数据。

对于每组测试数据，第一行包含整数 。

接下来 行，每行三个整数 ，表示 节点与 节点之间存在一条边，长度为 。

输出格式：

每组数据输出一个整数，表示权值总和最小值。

每个结果占一行。

数据范围：

完全图就是图中任意两个点之间都有边相连的图，不难计算出图中的边数为 。

还是先升序排序，对于取出的每个边——若该边可以被加入生成树中，它的两端节点一定分属于两个不同的连通块中。那么就在这两个连通块中互相连边（边的个数是 ），注意到原图是唯一的最小生成树，那么所连的边的边权就一定需要严格大于当前边的边权，即 。我们只需要开一个数组维护连通块大小即可。

注意到连通块大小的值仅在根节点有意义（根节点代表了整个连通块），就需要注意执行顺序的问题，并查集的合并函数一定在更新连通块大小之后。

1
2
3
4
5
6
7
8
9
10
for (int i = 1; i < n; i++) {
    int u = edges[i].u;
    int v = edges[i].v;
    int w = edges[i].w;
    if (!related(u, v)) {
        res += (s[find(u)] * s[find(v)] - 1) * (w + 1); // 维护的数值仅在根节点编号上有意义，因此以find()函数包裹下标获得根节点的编号
        s[find(v)] += s[find(u)]; // 合并连通块，大小相加，其中一个连通块的实际大小为0，恰好也解释了为什么一定需要传入根节点的下标
        merge(u, v); // 注意执行顺序！连通块大小更新之后才进行合并
    }
}

次小生成树

AcWing 1148 秘密的牛奶运输

题目地址：AcWing 1148

题目难度：中等

农夫约翰要把他的牛奶运输到各个销售点。

运输过程中，可以先把牛奶运输到一些销售点，再由这些销售点分别运输到其他销售点。

运输的总距离越小，运输的成本也就越低。

低成本的运输是农夫约翰所希望的。

不过，他并不想让他的竞争对手知道他具体的运输方案，所以他希望采用费用第二小的运输方案而不是最小的。

现在请你帮忙找到该运输方案。

注意：

  • 如果两个方案至少有一条边不同，则我们认为是不同方案；
  • 费用第二小的方案在数值上一定要严格大于费用最小的方案；
  • 答案保证一定有解；

输入格式：

第一行是两个整数 ，表示销售点数和交通线路数；

接下来 行每行 个整数 ，表示销售点 和销售点 之间存在线路，长度为 。

输出格式：

输出费用第二小的运输方案的运输总距离。

数据范围：

可能包含重边

对于非严格次小生成树，我们的求解策略如下：

  1. 正常跑一遍 算法得到最小生成树的边权和 。
  2. 遍历每个未选进生成树中的边，假设这个边的端节点是 和 ，边权为 ，那么求出生成树中 与 相连的权值最大的边（假设边权为 ）。用这条未选边去替换已有边，新生成树的权值就是 。
  3. 重复如上操作，不断对 取最小值。最终得到的最小值就是答案。

当用于替换的边权等于原边权时，最终得到的答案应该是等于 的，因此这个方法只能求解非严格次小生成树。那么对于严格次小生成树，我们的求解策略如下：

  1. 得到最小生成树的权值
  2. 遍历每一个不在最小生成树内的边，若边的权值 严格大于原图中该两点最大边权 ，则直接替换；否则，若 且新取边的边权严格大于原图中该两点的严格次大边权 ，就用 进行计算。两种情况得到的生成树权值分别为 和 。
  3. 重复如上操作，不断取最小值，得到答案。

当数据范围较小时，用 即可求出两点间的最长边权和次长边权。注意到前向星建双向边， 过程中应额外传入父节点编号以免反向搜索导致死循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
#include <bits/stdc++.h>

#define N 100010
#define M 300010
using namespace std;

typedef long long ll;

struct Graph {
    int to, ne, w;
} graph[M << 1];

struct Edge {
    int u, v, w;
    bool inTree;
} edges[M];

int p[N];
int h[N], idx = 0;
int dist1[N][N], dist2[N][N];

void add(int u, int v, int w) {
    idx++;
    graph[idx].to = v;
    graph[idx].ne = h[u];
    graph[idx].w = w;
    h[u] = idx;
}

int find(int x) {
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

void merge(int a, int b) {
    p[find(a)] = find(b);
}

bool related(int a, int b) {
    return find(a) == find(b);
}

bool cmp(const Edge &l, const Edge &r) {
    return l.w < r.w;
}

void dfs(int u, int fa, int max1, int max2, int arr1[], int arr2[]) {
    arr1[u] = max1;
    arr2[u] = max2;
    for (int i = h[u]; ~i; i = graph[i].ne) {
        int j = graph[i].to;
        if (j != fa) {
            int tmp1 = max1, tmp2 = max2;
            if (graph[i].w > tmp1) tmp1 = graph[i].w, tmp2 = max1;
            else if (graph[i].w < tmp1 && graph[i].w > tmp2) tmp2 = graph[i].w;
            dfs(j, u, tmp1, tmp2, arr1, arr2);
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    memset(h, -1, sizeof h);

    int n, m;
    cin >> n >> m;

    for (int i = 1; i <= n; i++) p[i] = i;
    for (int i = 1; i <= m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        edges[i].u = a;
        edges[i].v = b;
        edges[i].w = c;
        edges[i].inTree = false;
    }
    sort(edges + 1, edges + 1 + m, cmp);

    ll st = 0;
    for (int i = 1; i <= m; i++) {
        int u = edges[i].u;
        int v = edges[i].v;
        int w = edges[i].w;
        if (!related(u, v)) {
            merge(u, v);
            edges[i].inTree = true;
            st += w;
            add(u, v, w);
            add(v, u, w);
        }
    }

    for (int i = 1; i <= n; i++) dfs(i, 0, -INT_MAX, -INT_MAX, dist1[i], dist2[i]);

    ll ans = INFINITY;
    for (int i = 1; i <= m; i++) {
        if (edges[i].inTree) continue;
        int u = edges[i].u;
        int v = edges[i].v;
        int w = edges[i].w;
        if (w > dist1[u][v]) ans = min(ans, st + w - dist1[u][v]);
        else if (w > dist2[u][v]) ans = min(ans, st + w - dist2[u][v]);
    }
    cout << ans << endl;

    return 0;
}

对于较大的数据，正确的做法应是 倍增和 。在求解上述 和 的过程中效率更高，会优于 的指数级复杂度。

本页文档最后更新于：2024年6月15日

oi

算法

生成树

评论