抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

基础数据结构 树状数组

oi算法

发布于：2024年11月22日

字数：4.2k 字

时长：18 分钟

前言

我在第一次决定学树状数组前就预先接触过线段树的基本概念和操作，当时只觉得树状数组能做到的事情线段树也能做到。不仅如此，线段树朴素的二分思想在我看来是易于树状数组的 lowbit 规律的，综上种种，那时我便跳过了树状数组的学习。而如今接触到了各种线段树无法轻易解决的问题（偏序、逆序对等），才记起树状数组的各种好，经过再三斟酌，我决定还是简单学习一下树状数组。

基本概念

二进制分解

迄今为止我们已经接触过很多数字分解法，例如斐波那契数列的齐肯多夫表示法、基于算术基本定理的质因子拆分法、多重背包中用到的二进制分解法。在树状数组中，依然是信息学喜闻乐见的二进制来为之赋能，可以说树状数组就是完全搭建在二进制分解的基础上的。

对于一个自然数 ，它一定可以被分解为若干二次幂的和。即 。

根据这点，把 划成若干区间：

区间的大小分别为 。观察每个小区间的右端点 ，它们的二进制分解形式就是右端点的和式 ，那么这个区间的大小就是 ，幂数也就是 的二进制分解中最小元素的幂数，进而， 的二进制 0/1 表示中 1 的最小位置。

lowbit 算符

得到了规律，我们自然想要求出二进制最低位 1 的位置，实践中常用 lowbit 函数，它的定义是 x & -x。根据计算机处理负数的知识——负数的二进制相当于各位取反再加 1。较高位（比最低位 1 更高的所有位）在进行按位与运算时都会被消成 0，而较低位（不比最低位 1 更高的所有位）取反后均是 1，加上 1 之后会不断进位直到最低位 1 的位置（取反后为 0，进位后为 1），按位与运算就可以保留下这一位而消去其他位。结果就是 。例如：，因为 ；，因为 。

在 系统中，标准库还提供一个函数 ffs，即 Find First bit Set，它返回最低位 1 的位置，相当于对 lowbit 取以二为底的对数。

更多位运算相关库见 [奇技淫巧] C++ 编程小寄巧 GCC 内建函数的巧用

树状数组

来源：洛谷 @DWHJHY 树状数组 FENWICK TREE

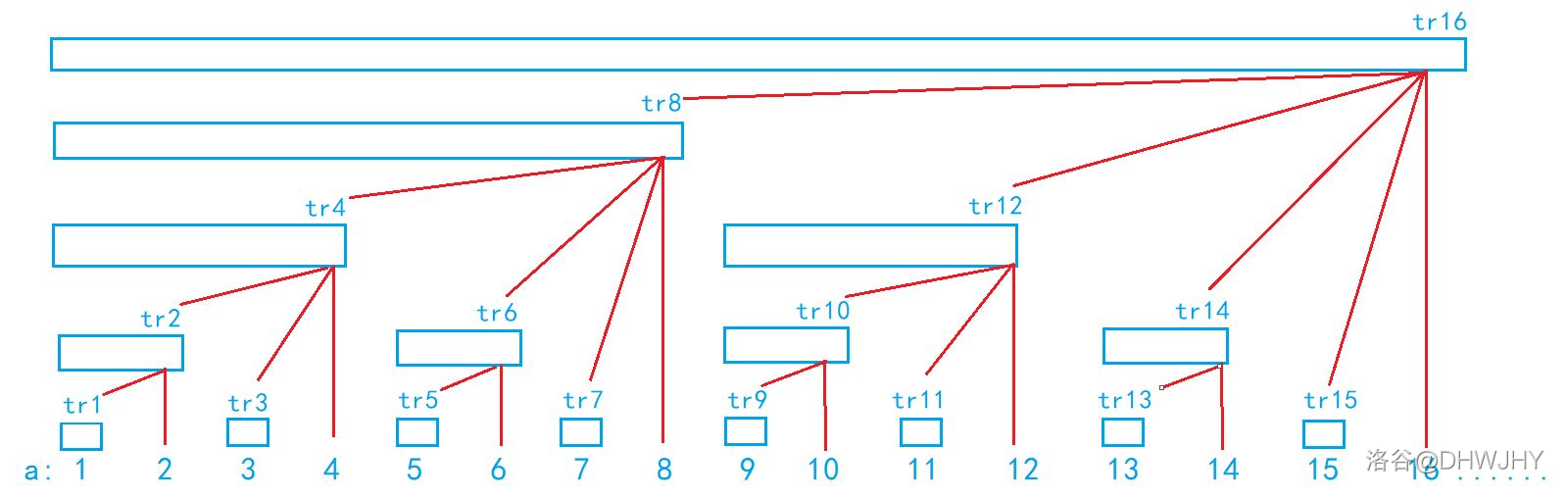
结合图示，我们把树状数组节点的几个性质讲解一下：

  1. 除根节点外，节点 的父节点是 。反之，满足 的所有节点 都是 的子节点。
  2. 节点 的子节点数为 。
  3. 令 ，不断递归计算 直到结果为 前的最后一个 值与先前的所有 值作为树状数组下标求和得到的总和即等于 的前缀和。（具体见区间查询部分）
  4. 树的深度为 ，当节点数不足 2 的整数次幂时结构为森林。

其实树状数组可以不用建树，而是直接维护前缀和。当我们对树状数组插入数据时（假设原数组为 ，树状数组为 ），像线段树的上传操作一样，我们从子节点开始不断向父节点进行更新，也就是不断对下标加上当前下标的 值直到超出 的范围。

1
2
3
void modify(int u, int x) {
    for (int i = u; i <= n; i += lowbit(i)) c[i] += x; // 不断跳到父节点并累加值
}

在统计时，用 和 的前缀和相减获得区间总和。

1
2
3
4
5
int query(int r) {
    int ret = 0;
    for (int i = r; i; i -= lowbit(i)) ret += c[i]; // 根据性质 3，求得 [1,r] 区间内的前缀和
    return ret;
}

以上两种便是树状数组的基本操作。

简单维护策略

前缀和

例题：CF755D

难度：提高+/省选-

给出一个 边形，和距离 。 第一次连接 和 ，第二次连接 和 ，依次进行 次，每次结束后输出 边形被分割成了几个区域。

互质，。

注意到每次连边对总区域数的贡献是该线段与已有线段的相交次数加一。我们的问题就转化成计算相交线段的个数。观察可得它其实就是端点 到 间经过的所有点的度数之和（多边形本身的边不计入度数），因此维护一个线段树/树状数组，每次询问 内的和，再对两端点的值加一即可。

题解同步于本站

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>
#define N 1000010
#define lowbit(x) (x & -x)
using namespace std;

typedef long long ll;

ll c[N];
int n;

void modify(int u) {
    for (int i = u; i <= n; i += lowbit(i)) c[i]++;
}

ll query(int R) {
    ll ret = 0;
    for (int i = R; i; i -= lowbit(i)) ret += c[i];
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int k;
    cin >> n >> k;
    k = min(k, n - k);
    ll section = 1;
    int pos = 1;
    for (int i = 1; i <= n; i++) {
        int R = pos + k; // 获得右端点
        ll sum;
        if (R > n) R %= n, sum = query(R - 1) + query(n) - query(pos); // 如果跨过 0 节点，特判
        else sum = query(R - 1) - query(pos); // 正常前缀和
        modify(pos); // 更改两个端点
        modify(R);
        section += sum + 1;
        pos = R;
        cout << section << ' ';
    }

    return 0;
}

实测树状数组的时间大约是线段树的四分之一。

差分

例题：P4939 Agent2

难度：普及/提高-

在线段树维护区间种类数一节中，我们已经探讨过利用差分数组和前缀和来解题的具体原理，树状数组亦然。树状数组维护可差分信息和小常数的天生特性使得它在这类题目中表现良好。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
#define N 10000010
#define lowbit(x) (x & -x)
using namespace std;

typedef long long ll;

int start[N], ed[N];
int n;

void modifyS(int u) {
    for (int i = u; i <= n; i += lowbit(i)) start[i]++;
}

void modifyE(int u) {
    for (int i = u; i <= n; i += lowbit(i)) ed[i]++;
}

int queryS(int u) {
    int ret = 0;
    for (int i = u; i; i -= lowbit(i)) ret += start[i];
    return ret;
}

int queryE(int u) {
    int ret = 0;
    for (int i = u; i; i -= lowbit(i)) ret += ed[i];
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int m;
    cin >> n >> m;
    while (m--) {
        int op, l, r;
        cin >> op >> l;
        if (op == 0) {
            cin >> r;
            modifyS(l);
            modifyE(r);
        } else cout << queryS(l) - queryE(l - 1) << endl;
    }

    return 0;
}

区间加+单点查询

例题：CF44C Holidays

难度：普及/提高-

如果本题没有保证 的话，它将会更加复杂。

轻易可以看出，我们需要对给出的区间进行区间加一，结束后枚举每个点的值是否恰好是 。在线段树区间加等差数列一节中，我们给出了将原序列转化为差分序列、将区间加等差数列转化成区间两端点的单点操作的解决方案。本题要求区间加一个常数列，即特殊的等差数列。实际维护方法和线段树是相同的——左端点加上首项，右端点右侧第一个点减去末项，本题中首项末项均为 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
#define N 110
#define lowbit(x) (x & -x)
#define START 0
#define END 1
using namespace std;

int n;
int c[N];

void modify(int u, int x) {
    for (int i = u; i <= n; i += lowbit(i)) c[i] += x;
}

int query(int u) {
    int ret = 0;
    for (int i = u; i; i -= lowbit(i)) ret += c[i];
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int m;
    cin >> n >> m;
    while (m--) {
        int l, r;
        cin >> l >> r;
        modify(l, 1);
        if (r < n) modify(r + 1, -1); //树状数组其实无需判断边界，但是线段树是必需的
    }
    for (int i = 1; i <= n; i++) {
        if (query(i) ^ 1) {
            cout << i << ' ' << query(i) << endl;
            return 0;
        }
    }
    cout << "OK" << endl;

    return 0;
}

权值树状数组

普通的树状数组维护的信息（原序列前缀和/差分）有时不能满足我们的多样化需求，此时权值树状数组便应运而生。它类似于桶，通过维护原序列中每个数的出现次数来化简一些比较棘手的问题。在原序列值域很大，或者是只关心元素间相对大小关系时十分有用。

逆序对

例题：P1908 逆序对

难度：普及/提高-

逆序对的定义是：对于给定的一段正整数序列，逆序对就是序列中 且 的有序对。给定一段长度为 的数列，求出逆序对的数量。

我们只关心元素间的大小关系，符合权值树状数组的使用范畴，因此离散化并建立之。接下来是如何处理逆序对的问题。

考虑将待插入数列升序排序（第二关键字为下标升序）然后依次插入。假如原序列中 最小，它将被第一个插入，具体是在树状数组的 位置增加 并向上更新。数字是从小到大插入的，因此逆序对只会出现在 位后面， 减去 内的前缀和即为答案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <bits/stdc++.h>
#define N 500010
#define lowbit(x) (x & -x)
using namespace std;

typedef long long ll;
typedef pair<ll, int> PII;

ll c[N];
PII a[N];
int rnk[N];
int n;

bool cmp(const PII &l, const PII &r) {
    return l.first == r.first ? l.second < r.second : l.first < r.first;
}

void add(int u, int x) {
    for (int i = u; i <= n; i += lowbit(i)) c[i] += x;
}

ll query(int l) {
    ll sum = 0;
    for (int i = l; i; i -= lowbit(i)) sum += c[i];
    return sum;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i].first, a[i].second = i;
    sort(a + 1, a + n + 1, cmp);
    for (int i = 1; i <= n; i++) rnk[a[i].second] = i;
    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        add(rnk[i], 1);
        ans += i - query(rnk[i]);
    }
    cout << ans << endl;

    return  0;
}

区间第 k 大问题

例题：P1168 中位数

难度：普及+/提高

权值树状数组的一个强力应用就是求解区间第 大。

由题可知，有 个元素的数列的中位数就是它的第 大元素。我们只需在读入奇数个数时输出已有区间的第 大即可。因而问题简化成求解区间第 大。首先对输入数据离散化，然后据此建立权值树状数组。

在权值树状数组上，我们要求最小的 使得 且 成立，此时第 项即为所求。一般来说，我们会想到二分 ，这样的时间复杂度是 ，数据大时无法通过。

此时我们借助树状数组下标之间的关系，进一步优化二分过程。事实上，我们选择用倍增来替代二分。这个做法其实是基于树状数组下标与 lowbit 值之间的恒等关系：对于区间 ，它的区间和是 。

具体流程如下：

  1. 令区间 的前缀和 ，待求答案 。
  2. 让 从 开始倒序循环到 。
  3. ，检查此时的 是否超出边界 ，或者是 的前缀和 是否非严格大于 。若是，则撤销此次倍增，还原 ；否则保留更改，同时 。
  4. 循环结束后，返回 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
#define N 100010
#define lowbit(x) (x & -x)
using namespace std;

typedef long long ll;

int n;
int a[N], b[N];
ll c[N];
int cnt = 0;

void modify(int u, int x) {
    for (int i = u; i <= cnt; i += lowbit(i)) c[i] += x;
}

int query(int k) {
    ll s = 0;
    int x = 0;
    for (int i = log2(cnt) + 1; i >= 0; i--) { // 倍增
        x += 1 << i; // 尝试倍增
        if (x > cnt || s + c[x] >= k) x -= 1 << i; // 不符合要求，撤销倍增
        else s += c[x]; // 保留倍增，更新前缀和
    }
    return x + 1;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], b[i] = a[i];
    sort(a + 1, a + 1 + n);
    cnt = unique(a + 1, a + 1 + n) - a - 1;
    for (int i = 1; i <= n; i++) b[i] = lower_bound(a + 1, a + 1 + n, b[i]) - a; // 排序去重离散化
    for (int i = 1; i <= n; i++) {
        modify(b[i], 1);
        if (i & 1) cout << a[query(i + 1 >> 1)] << endl;
    }

    return 0;
}

三元序列问题

例题：P10589 楼兰图腾

难度：普及+/提高

根据乘法原理，对于某个点 ，它能构成的符合要求的 V 形三元组的总数是它左侧严格大于它的点的数量乘以它右侧严格大于它的点的数量，反之亦然。问题转化成了如何维护某个点左右两侧比它大/小的点的总数。

同样是先离散化建立两个权值树状数组，一个维护左侧信息、另一个维护右侧信息。在维护左侧相关信息时按正序添加节点。因为权值线段树维护一段升序序列，因此先加入（在左侧）、且比当前点小的点的数量就是 的前缀和；对应的，因为已经添加了 个数，在左侧又有 个数小于等于 ，那么在左侧且比它大的数就共有 个。这也是树状数组维护逆序对的思路。

维护右侧点就换个顺序，倒序添加节点。基本思路和维护左侧节点相同。维护右侧比它小的节点数时，显然就是前缀和；而求解右侧比它大的节点数时，因为右侧已经有 个节点，又有 个比它小，那么相减即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>
#define N 200010
#define lowbit(x) (x & -x)
using namespace std;

typedef long long ll;

int n;
int a[N], b[N];
int L1[N], R1[N], L2[N], R2[N];
int c1[N], c2[N];

void modify(int c[], int u, int x) {
    for (int i = u; i <= n; i += lowbit(i)) c[i] += x;
}

int query(int c[], int u) {
    int ret = 0;
    for (int i = u; i; i -= lowbit(i)) ret += c[i];
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i], b[i] = a[i];
    sort(a + 1, a + 1 + n);
    for (int i = 1; i <= n; i++) b[i] = lower_bound(a + 1, a + 1 + n, b[i]) - a;
    for (int i = 1; i <= n; i++) {
        modify(c1, b[i], 1);
        L1[i] = query(c1, b[i] - 1); // 左侧比它小
        L2[i] = i - query(c1, b[i]); // 左侧比它大
    }
    for (int i = n; i; i--) {
        modify(c2, b[i], 1);
        R1[i] = n - i - query(c2, b[i]) + 1; // 右侧比它大
        R2[i] = query(c2, b[i] - 1); // 右侧比它小
    }
    ll ans1 = 0, ans2 = 0;
    for (int i = 1; i <= n; i++) {
        ans1 += 1ll * L2[i] * R1[i];
        ans2 += 1ll * L1[i] * R2[i];
    }
    cout << ans1 << ' ' << ans2 << endl;

    return 0;
}

维护动态规划

在动态规划中，善用各种数据结构，有时可以将暴力转移的时间复杂度除以一个 。例如单调数据结构优化、斜率优化等。这里将介绍树状数组在维护动态规划权值上的一些应用。

k 元严格上升子序列计数

例题：UVA12983 The Battle of Chibi

难度：普及+/提高

设状态为 表示长度为 且以 结尾的 元最长上升子序列的个数。转移就是 ，但是总时间复杂度是 的，不能接受。

注意到 产生贡献当且仅当 。可以先将 离散化，当一个状态 完全转移完之后，我们把它的值加到 对应的位置上。运算 时，就可以把排名前 的和加入进来，刚好就涵盖了所有小于 对应的 的值。因此建立树状数组维护即可，时间复杂度成功降落到 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
#define N 1010
#define MOD 1000000007
#define lowbit(x) (x & -x)
using namespace std;

typedef long long ll;

int n;
int a[N], b[N];
ll c[N], dp[N][N];

void modify(int u, ll x) {
    for (int i = u; i <= n; i += lowbit(i)) c[i] += x;
}

ll query(int u) {
    ll ret = 0;
    for (int i = u; i; i -= lowbit(i)) ret += c[i];
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t;
    cin >> t;
    for (int x = 1; x <= t; x++) {
        memset(dp, 0, sizeof dp);

        int m;
        cin >> n >> m;
        for (int i = 1; i <= n; i++) cin >> a[i], b[i] = a[i];
        sort(a + 1, a + 1 + n);
        unique(a + 1, a + 1 + n) - a - 1;
        for (int i = 1; i <= n; i++) b[i] = lower_bound(a + 1, a + 1 + n, b[i]) - a + 1; // 让排名全严格大于 1
        for (int i = 1; i <= n; i++) {
            memset(c, 0, sizeof c); // 树状数组记录每个 i 对应的值，因此 i 变化后树状数组也要清空
            if (i == 1) modify(1, 1); // 相当于 dp[0][0] = 1
            for (int j = 1; j <= n; j++) {
                dp[i][j] = (dp[i][j] + query(b[j] - 1)) % MOD; // 无需再枚举之前比它小的点，直接加上贡献即可
                modify(b[j], dp[i - 1][j]); // 将小于 b[j] 的点的贡献加入树状数组
            }
        }
        ll sum = 0;
        for (int i = 1; i <= n; i++) sum = (sum + dp[m][i]) % MOD; // 对所有长度为 m 的序列个数求和
        cout << "Case #" << x << ": " << sum << endl;
    }

    return 0;
}

```

本页文档最后更新于：2024年11月28日

算法

oi

数据结构

评论