抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

IDA* ——启发式迭代加深搜索算法

oi算法

发布于：2024年5月17日

字数：2.8k 字

时长：11 分钟

A-star，迭代加深搜索以及 IDA-star

我们先前在 这篇文章 中探讨了 A* 算法以及其实现思路。回顾一下，A* 算法为普通的搜索算法加上了一个名为估价函数的设置，使得 A* 能够在搜索时不会那么偏离正确答案（最短路径）。从而大幅改善了普通 BFS 的近似穷举的低效策略。

而迭代加深就有些“取巧”了。万一某一天，你碰到了一位出生很有底子的出题人。他出了一道搜索题，但是他故意设置了很多很深很深的子树用来卡你的 BFS 和 A，这时你发现答案往往都在浅层，那么先前你的算法在深子树上做的一切工夫不就全白费了吗？于是迭代加深搜索应运而生，它限制每次搜索的最大深度，每次只从根节点开始向下搜索对应层数，若没找到答案，则继续加大最大深度；若找到了位于浅层的答案，直接返回，效率就会比普通的 BFS 与 A 快不少。

而 IDA* 则是它的改进版，其中 ID 指 Iterative Deepening，即迭代加深。因此 IDA* 又叫做“迭代加深的 A* 算法”（启发式迭代加深搜索）。顾名思义，它将二者有机结合起来。每次限定一个最大深度向下搜索，配合来自 A* 的估价函数进行最优性剪枝，进一步提效。简直不要太爽。

迭代加深的执行效率

有些人会问，每次加大迭代层数，程序都会从根节点重新开始扫描，那岂不是浪费了很多效率？

我们先从一个简单的完全二叉树开始分析：

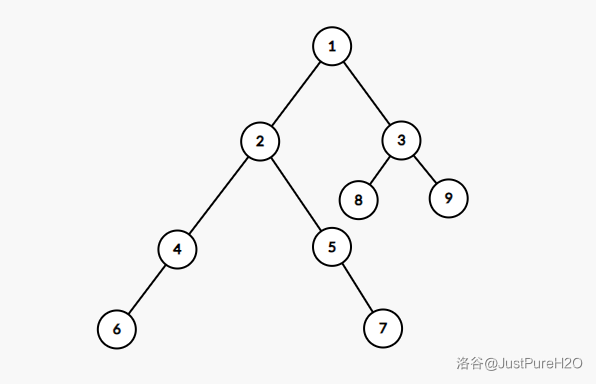
根据完全二叉树的性质，搜素第一层需要扫描 个节点（根节点）；第二层则需要扫描 个节点；第三层是 个……以此类推，第 层就是 个。根据等比数列的求和公式，搜索 次，总共搜索了 个节点（包含重复搜索）——其中前 次的节点数共 个，约为总数的一半。然而，实际题目中可能出现三叉树、四叉树等等多叉的树形结构。假设利用迭代加深思想搜索一颗满 叉树，并令最大层数由 迭代到 一共需要搜索的节点数为 个（重复搜索也计入），那么随着 的增大， 的值将越来越小，也就是说前面 层搜索的复杂度在第 次搜索的复杂度面前就相形见绌了，即 。迭代加深搜索的复杂度基本和搜索 层的复杂度相差无几，因此以上的担心是没必要的。

典型例题

洛谷 P10488 Booksort

题目传送门：这里

题目难度：普及/提高+

给定 本书，编号为 。

在初始状态下，书是任意排列的。

在每一次操作中，可以抽取其中连续的一段，再把这段插入到其他某个位置。

我们的目标状态是把书按照 的顺序依次排列。

求最少需要多少次操作。

输入：

第一行包含整数 ，表示共有 组测试数据。

每组数据包含两行，第一行为整数 ，表示书的数量。

第二行为 个整数，表示 的一种任意排列。

同行数之间用空格隔开。

输出：

每组数据输出一个最少操作次数。

如果最少操作次数大于或等于 次，则输出 5 or more。

每个结果占一行。

数据范围

我们从什么地方看出需要使用 IDA*？首先，搜索空间较大：根据数据范围，书本最多有 本，每次可以选择 本任意插入其他位置，运用插空法，最大可能的状态总数就是 ，严重超限；第二就是答案的位置浅：根据题目，当移动次数大于等于 时就可以直接特判退出了，因此我们只需要在前 层寻找答案即可。

既然是 IDA*，我们就需要设计估价函数。因为最终需要排成上升序列，每次操作最多更改一个地方的单调性。因此遍历给定的序列，当某个元素的后继节点不在本来的位置（表现为 ）时累加估价，返回即可。

对于状态搜索，考虑枚举每次移动的段的长度，然后在该段末尾至整个序列末尾的可插入位置中枚举段插入的位置，通过模拟得到插入后的序列即可。注意要及时恢复现场！

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>

#define N 20

using namespace std;
typedef long long ll;

int n;
int a[N], cpy[5][N];

int f() {
    int res = 0;
    for (int i = 1; i < n; i++) {
        if (a[i] + 1 != a[i + 1]) res++;
    }
    return (int) ((res + 2) / 3);
}

void out() {
    for (int i = 1; i <= n; i++) cout << a[i] << ' ';
    cout << endl;
}

bool ida(int now, int max_d) {
    if (now + f() > max_d) return false;
    if (!f()) return true;
    for (int len = 1; len <= n; len++) { // 段长度 
        for (int j = 1; j <= n - len + 1; j++) { // 段起始下标
            int seg_end = len + j - 1; // 段终止下标
            for (int k = seg_end + 1; k <= n; k++) { // 插入到下标k的元素后面
                memcpy(cpy[now], a, sizeof a);
                int y = j;
                for (int x = seg_end + 1; x <= k; x++, y++) a[y] = cpy[now][x];
                for (int x = j; x <= seg_end; x++, y++) a[y] = cpy[now][x];
                if (ida(now + 1, max_d)) return true;
                memcpy(a, cpy[now], sizeof cpy[now]);
            }
        }
    }
    return false;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        int dep = 0;
        cin >> n;
        for (int i = 1; i <= n; i++) cin >> a[i];
        while (!ida(0, dep) && dep < 5) dep++;
        if (dep == 5) cout << "5 or more" << endl;
        else cout << dep << endl;
    }

    return 0;
}

UVA 1343 The Rotation Game (旋转游戏)

题目传送门：这里

题目难度：提高+/省选-

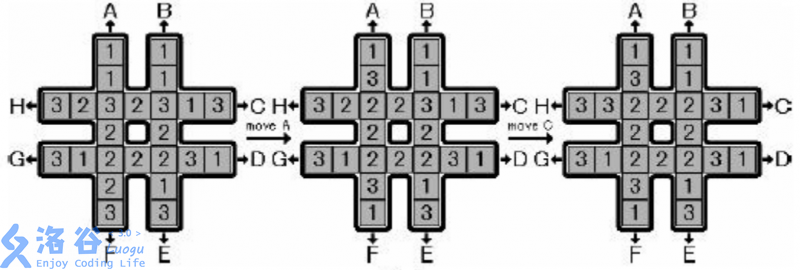
　　如图 所示，有一个 “#” 形的棋盘，上面有 三种数字各 个。给定 种操作，分别为图中的 。这些操作会按照图中字母与箭头所指明的方向，把一条长度为 的序列循环移动 个单位。例如下图最左边的 “#” 形棋盘执行操作 时，会变为图中间的 “#” 形棋盘，再执行操作 后会变为图中最右边的 “#” 形棋盘。

现给定一个初始状态，请使用最少的操作次数，使 “#” 形棋盘最中间的 个格子里的数字相同。

图1

输入格式：

输入包括不超过 组测试数据。每个测试数据只包括一行，包含 个整数，每相邻两个整数之间用 个空格隔开，表示这个 “#” 形棋盘的初始状态。（这些整数的排列顺序是从上至下，同一行的从左至右。例如 表示图 最左边的状态。）每两组测试数据之间没有换行符。输入文件以一行 结束。

输出格式：

　　对于每组测试数据，输出两行。第一行用字符 输出操作的方法，每两个操作字符之间没有空格分开，如果不需要任何步数，输出 No moves needed。第二行输出最终状态中最中间的 个格子里的数字。如果有多组解，输出操作次数最少的一组解；如果仍有多组解，输出字典序最小的一组。任意相邻两组测试数据的输出之间不需输出换行符。

这道题同样具有巨大的搜索空间，它的合法操作都有整整八种；但是答案可能位于较浅的层，具体表现在——每种操作若进行 次，那么就相当于执行它的反操作一次，显然没有必要以小换大，应用到八种操作里，就是答案层数不会超过 。因此可以以这点为硬限制进行迭代加深搜索。

观察到题目要求我们输出字典序最小的合法方案，只需要在搜索时按字典顺序循环搜索就好。对于剪枝，若上一次操作是将第三行整体向左滚动，那么当前层就显然不能将这一层向右滚动（滚了个寂寞）因此在函数签名里加上一个记录上一次操作的变量即可。

读入时为了直观（切合图中的结构），我选择使用二维数组存储 个数字，但这也带来了不小的代码量（逆天条件判断，我一开始用 switch 语句代码更长）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
#include <bits/stdc++.h>

#define N 10
using namespace std;

int a[N][N], cpy[55][N][N];
char seq[55];

int f() {
    int cnt[4];
    memset(cnt, 0, sizeof cnt);
    for (int i = 3; i <= 5; i++) cnt[a[3][i]]++, cnt[a[5][i]]++;
    cnt[a[4][3]]++, cnt[a[4][5]]++;
    return 8 - max(max(cnt[1], cnt[2]), cnt[3]);
}

bool check() {
    int piv = a[3][3];
    return (a[3][4] == piv && a[3][5] == piv && a[4][3] == piv && a[4][5] == piv && a[5][3] == piv && a[5][4] == piv &&
            a[5][5] == piv);
}

void vertical_scroll(bool lCol, bool up) {
    if (lCol) {
        if (up) for (int i = 1; i < 7; i++) swap(a[i][3], a[i + 1][3]);
        else for (int i = 7; i > 1; i--) swap(a[i][3], a[i - 1][3]);
    } else {
        if (up) for (int i = 1; i < 7; i++) swap(a[i][5], a[i + 1][5]);
        else for (int i = 7; i > 1; i--) swap(a[i][5], a[i - 1][5]);
    }
}

void horizontal_scroll(bool uRow, bool left) {
    if (uRow) {
        if (left) for (int i = 1; i < 7; i++) swap(a[3][i], a[3][i + 1]);
        else for (int i = 7; i > 1; i--) swap(a[3][i], a[3][i - 1]);
    } else {
        if (left) for (int i = 1; i < 7; i++) swap(a[5][i], a[5][i + 1]);
        else for (int i = 7; i > 1; i--) swap(a[5][i], a[5][i - 1]);
    }
}

void operate(char op) {
    switch (op) {
        case 'A':
        case 'B':
        case 'E':
        case 'F':
            vertical_scroll((op == 'A' || op == 'F'), (op == 'A' || op == 'B'));
            break;
        default:
            horizontal_scroll((op == 'C' || op == 'H'), (op == 'H' || op == 'G'));
            break;
    }
}

bool ida(int now, int max_dep, char last) {
    if (now + f() > max_dep) return false;
    if (check()) return true;
    for (int i = 0; i <= 7; i++) {
        if (now && last != '\0') {
            if (last == 'A' && i == 5) continue;
            if (last == 'F' && i == 0) continue;
            if (last == 'B' && i == 4) continue;
            if (last == 'E' && i == 1) continue;
            if (last == 'C' && i == 7) continue;
            if (last == 'H' && i == 2) continue;
            if (last == 'D' && i == 6) continue;
            if (last == 'G' && i == 3) continue;
        }
        memcpy(cpy[now], a, sizeof a);
        operate((char) (i + 'A'));
        seq[now] = (char) (i + 'A');
        if (ida(now + 1, max_dep, (char) (i + 'A'))) return true;
        memcpy(a, cpy[now], sizeof cpy[now]);
    }
    return false;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int x = 0, cnt = 0;
    while (cin >> x && x) {
        cnt++;
        if (cnt == 25) {
            cnt = 1;
            memset(seq, 0, sizeof seq);
        }

        if (cnt == 1) a[1][3] = x;
        else if (cnt == 2) a[1][5] = x;
        else if (cnt == 3) a[2][3] = x;
        else if (cnt == 4) a[2][5] = x;
        else if (cnt == 12) a[4][3] = x;
        else if (cnt == 13) a[4][5] = x;
        else if (cnt == 21) a[6][3] = x;
        else if (cnt == 22) a[6][5] = x;
        else if (cnt == 23) a[7][3] = x;
        else if (cnt == 24) a[7][5] = x;
        else if (cnt >= 5 && cnt <= 11) a[3][cnt - 4] = x;
        else if (cnt >= 14 && cnt <= 20) a[5][cnt - 13] = x;

        if (cnt == 24) {
            if (check()) cout << "No moves needed" << endl;
            else {
                int dep = 1;
                while (!ida(0, dep, '\0') && dep < 50) dep++;
                cout << seq << endl;
            }
            cout << a[3][3] << endl;
        }
    }
    return 0;
}

本页文档最后更新于：2024年5月29日

搜索算法

oi

算法

评论