物竞天择 遗传算法

前言

遗传算法Genetic Algorithm，简称 GA。是一种基于随机化的最优解搜索算法，它和模拟退火Simulate Anneling都基于随机化，遗传算法通过模拟自然界生物的遗传和变异、自然选择和淘汰的过程来找到最优种群（最优解）；后者则是通过设定一个初始温度以及降温率、将当前最优解进行随机扰动以寻得更优的解来找到最优解。

（纯属虚构）遗传算法就好比生活在中原地区的 OIer 们，竞赛主办方希望筛选出“随机化算法调参能力最强的一批选手”。于是官方从今年起，将复试的四道试题全部换成了需要模拟退火才能解决的问题，并且严格卡精度和时限。这样一来，调参能力弱的选手大多在复试中遗憾落榜，剩下的大部分都是调参能力强的选手……如此几年之后，官方会惊奇地发现全国选手的调参能力都有了大幅提升，最佳选手同样可以通过逐渐严格的要求来筛选出来。

相比之下，遗传算法适合解决复杂的离散与组合优化问题，在问题规模较大、搜索空间复杂时表现良好。

生物术语

学遗传算法首先就需要搞清楚它背后的基本生物学概念（都是高一内容，请放心食用）：

个体和种群：生命系统的其中两级结构层次，前者是指单一的生物体；后者则是指同一时间在一定区域内生活的同种生物的全部个体（同一时间、一定区域、同种生物、全部个体）
染色体：由组蛋白和缠绕的 DNA 双链构成，是遗传信息的载体
基因型：某个体全部基因组合的总称，可以理解为个体的基因组成
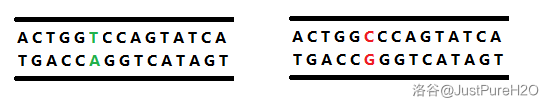
互换（基因重组）、基因突变：前者发生在减数分裂的前期，指在一对联会的同源染色体（四分体）间发生染色体相应片段的交换；后者是指基因发生的部分碱基对的改变
自然选择：来自达尔文进化论。他主张种群间存在生存斗争，有利突变积累得更多的个体有更大的几率在斗争中存活下来并将这些有利突变遗传给后代。即“物竞天择，适者生存”

以下几张图可以帮助你更轻松的理解这些概念：

互换：

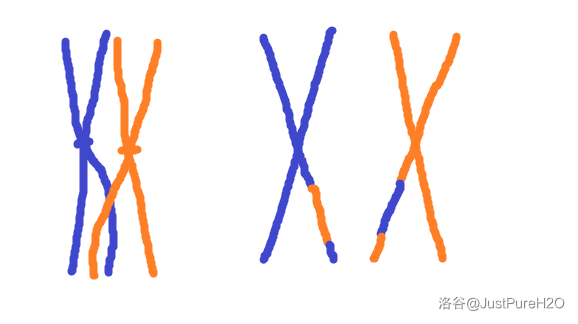
基因突变：

算法基本流程

适应性描述

我们引入一个适应性函数表示当前种群在当前环境下的生存表现，分数越高的种群就越有可能在此轮将当前代的优良基因遗传下去，即参与下一轮迭代。而随着迭代次数的增加，每一代的平均表现值会增加，当找到我们想要的优良后代时，停止这个算法，并宣布我们已经找到了一个令人满意的解。

的计算因题而异。在费马点的求解中，它可以是当前点到其他点的欧几里得距离之和；在最优化排列问题中，它可以是当前排列的总贡献、也可以是当前排列与标准排列之间的元素差距……总之，这个函数需要能定量地描述当前解与标准解之间的差距。

基因的突变和重组

遗传算法的一大乐趣就是模拟“遗传”和“变异”的过程。我们考虑把整个染色体编码成一个 0/1 串（实数串也是可行的），每一位代表一个基因，整个个体就可以看作是一个染色体集合（二进制串集合）。遗传时按照均等概率从父方和母方继承基因、变异过程也能通过随机取反某一位实现。

双亲杂交的代码实现如下（C++17 标准）：

// 整数版本 - LENGTH 宏记录整数的二进制最高包含多少位
[[nodiscard]] Individual hybrid(Individual p) const {
    int child = 0;
    for (int i = 0; i <= LENGTH; i++) {
        if (rand(1, 100) <= 50) child |= (gene >> i);
        else child |= (p.gene >> i);
    }
    return Individual(child);
}

// 字符串版本
[[nodiscard]] Individual hybrid(Individual p) const {
    string child;
    size_t len = gene.length();
    for (int i = 0; i < len; i++) {
        if (rand(1, 100) <= 50) child[i] = gene[i];
        else child[i] = p.gene[i];
    }
    return Individual(child);
}

个体突变的代码实现如下（C++17 标准）：

// 整数版本 - LENGTH 宏记录整数的二进制最高包含多少位
void mutate() {
    int times = rand(1, 3); // 突变 1~3 个基因，可调
    for (int i = 1; i <= times; i++) {
        int pos = rand(0, LENGTH);
        gene ^= (1 << pos);
    }
}

// 字符串版本
void mutate() {
    int times = rand(1, 3);
    for (int i = 1; i <= times; i++) {
        int pos = rand(0, gene.length() - 1);
        gene[pos] = (gene[pos] == '0' ? '1' : '0');
    }
}

优解的筛选与继承

算法开始时，我们会创建一个虚拟种群，种群大小是一个参数，一般在内。对于每一代，我们都在种群中随机选择个体杂交得到子一代。

和模拟退火一样，我们计算一下子代的适应参数，如果与亲代相比有了进步，那我们就毫不犹豫地让它生存下去；反之，这个子代是有一定几率能生存下去的，我们让这个概率遵循准则，即，取是比较明智的。

那如何最大化解的最优性呢？可以使用不同的随机算子，常用的几种随机算子如下：

最佳保留选择

这是为了最小化不定向变异和随机遗传带来的优良性状丢失所设计的选择算子。

首先把父代集合按照适应性进行降序排列，选取最靠前的若干个体，并让它们直接拿到进入下一代的入场券。然后再从排名相对靠前的亲代个体中选择个体杂交，并继承到子代。

因为代码实现简单、排序的时间复杂度相对较低、保证继承优良性状、有效减少随机性损失、维持了最基本的基因多样性，因此这是最常用的选择算子之一。

轮盘赌选择

类似于分层抽样调查的原理。首先计算出种群内所有个体的适应度之和，接下来对于每个个体，被选中的概率可以通过如下公式导出：

此后再进行随机，按照计算出的概率分配名额即可。实现难度较最佳保留选择较大，而且这种选择算子造成的选择误差也会更大一些。

随机竞争选择

每次用轮盘赌选择选出两个个体，并让二者进行竞争，适应度大的保留，选入下一代，直到满额为止。这种方法的时间复杂度较高，但是能比较有效的保留亲代优良性状。

因为最佳保留选择算子的实现简单、效果较好，因此下面给出最佳保留选择的实现代码：

// MAX_POPULATION 是种群的最大个体数；MAX_ADAPTION 作用是让父代表现优异的保送进下一代；MAX_ACCEPTANCE 用来设置父代生存能力排名的上限
vector<Individual> initP; // 初始种群
for (int i = 1; i <= MAX_POPULATION; i++) initP.emplace_back(rand(0, 1000000), rand(0, 1000000));
for (int T = 10; T; T--) {
    // 繁衍 10 代，可调
    vector<Individual> curP; // 子代
    sort(initP.begin(), initP.end()); // 排序
    for (int i = 0; i <= MAX_ADAPTION; i++) curP.push_back(initP[i]); // 保送
    while (curP.size() < MAX_POPULATION) {
        Individual p = initP[rand(0, MAX_ACCEPTANCE)]; // 选出父代
        Individual child = p.hybrid(initP[rand(0, MAX_ACCEPTANCE)]); // 杂交得到子代
        if (rand(0.0, 1.0) <= 0.02) child.mutate(); // 2% 的几率突变个别基因，几率可调
        double x = child.fit, y = p.fit;
        double delta = x - y;
        if (delta < 0 || exp(-delta / T) / 2.0 > rand(0.0, 1.0)) curP.push_back(child); // 优胜劣汰
    }
    initP = curP; // 更新种群
}

典型例题

UVA 10228 / POJ 2420 - A Star not a Tree? / AcWing 3167 星星还是树

题目地址：UVA 10228/POJ 2420/AcWing 3167

题目难度：普及+/提高

题面来源于 AcWing

在二维平面上有个点，第个点的坐标为。

请你找出一个点，使得该点到这个点的距离之和最小。

该点可以选择在平面中的任意位置，甚至与这个点的位置重合。

输入格式：

第一行包含一个整数。

接下来行，每行包含两个整数，表示其中一个点的位置坐标。

输出格式：

输出最小距离和，答案四舍五入取整。

数据范围：

请注意，UVA 题目的输出有细微不同！

这道题是一道求解平面费马点的模板问题。我们把当前点的坐标设计成基因，由于题目要求保留整数，为了精度，坐标需要保留到两位小数，考虑到，我们可以把这个数设置成以内的整数，在计算时除以即可；在设计适应性函数时，我们就选用当前点到其他点的距离之和；稍微调整一下参数，我们就可以过掉这个题。为了方便，这里转而使用父代自交的方法产生子代。

#include <bits/stdc++.h>

#define N 110
#define MAX_POPULATION 500
#define MAX_ADAPTION 30
#define MAX_ACCEPTANCE 50
using namespace std;

typedef pair<double, double> PDD;

PDD a[N];
int n;
random_device rd;
double ans = 1e9;

double rand(double l, double r);
double dis(PDD i, PDD j);
int rand(int l, int r);

struct Individual {
    int x, y;
    double fit;

    Individual(int x, int y) : x(x), y(y) {
        fit = fitness();
    }

    [[nodiscard]] double fitness() const {
        double sum = 0;
        for (int i = 1; i <= n; i++) {
            sum += dis((PDD) {(double) x / 100, (double) y / 100}, a[i]);
        }
        return sum;
    }

    [[nodiscard]] Individual hybrid() const {
        int x1 = x, y1 = y;
        int t = rand(0, 3);
        for (int i = 1; i <= t; i++) {
            int pos = rand(0, 20);
            x1 ^= (1 << pos);
        }
        t = rand(0, 3);
        for (int i = 1; i <= t; i++) {
            int pos = rand(0, 20);
            y1 ^= (1 << pos);
        }
        return {x1, y1};
    }

    void mutate() {
        for (int i = 1; i <= 3; i++) x ^= (1 << rand(0, 20));
        for (int i = 1; i <= 3; i++) y ^= (1 << rand(0, 20));
    }

    bool operator<(const Individual &p) const {
        return fit < p.fit;
    }
};

double dis(PDD i, PDD j) {
    return sqrt((i.first - j.first) * (i.first - j.first) + (i.second - j.second) * (i.second - j.second));
}

double rand(double l, double r) {
    if (r < l) return 0;
    return (double) rd() / random_device::max() * (r - l) + l;
}

int rand(int l, int r) {
    if (r < l) return 0;
    return (int) (rd() % (r - l + 1)) + l;
}

void GA() {
    vector<Individual> initP;
    for (int i = 1; i <= MAX_POPULATION; i++) initP.emplace_back(rand(0, 1000000), rand(0, 1000000));
    for (int T = 10; T; T--) {
        vector<Individual> curP;
        sort(initP.begin(), initP.end());
        for (int i = 0; i <= MAX_ADAPTION; i++) curP.push_back(initP[i]);
        while (curP.size() < MAX_POPULATION) {
            Individual p = initP[rand(0, MAX_ACCEPTANCE)];
            Individual child = p.hybrid();
            if (rand(0.0, 1.0) <= 0.02) child.mutate();
            double x = child.fit, y = p.fit;
            double delta = x - y;
            if (delta < 0 || exp(-delta / T) / 2.0 > rand(0.0, 1.0)) curP.push_back(child);
        }
        initP = curP;
    }
    ans = initP[0].fitness();
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t;
    cin >> t;
    for (int i = 1; i <= t; i++) {
        ans = 1e9;
        cin >> n;
        for (int j = 1; j <= n; j++) cin >> a[j].first >> a[j].second;
        GA();
        cout << (int) round(ans) << endl;
        if (i ^ t) cout << endl;
    }
    return 0;
}

P7812 [JRKSJ R2] - Dark Forest

题解同步

题目地址：P7812

题目难度：省选/NOI-

题目类型：提交答案

本题为提交答案题。

给你一个长为的序列，定义的排列的权值为

你可以理解为这个排列是一个环，即。

请构造一个权值尽量大的的排列。

输入格式：

第一行一个整数。

第二行个整数表示序列。

输出格式：

一行个整数表示排列。

数据范围：

对于的数据，。

注意事项：

本题使用 Special Judge，每个测试点都有个参数。如果你的输出的权值，则该测试点您至少会获得分。

特别的，如果您的输出不是一个的排列，您会在该测试点获得分。

附件下载：

评分参数

输入数据

因为我选择本地测评再提交打表程序（~~太菜了不知道怎么提交答案~~），所以本地我会开 O3 优化、以及循环展开之类的编译预处理指令。

数据点还是好做的，直接模拟退火能过，没有时限的话把参数卡死一点是没问题的。

数据点很有意思，输入是一个单增排列，我们优先让大数乘大数，构造一个两边大中间小的特殊构造即可。

数据点就开始上强度了，模拟退火怎么卡精度都过不去，同机房的退火大佬好像跑了几天？总之对于这种毒瘤测试点，我们上遗传算法。

实现整个种群太过麻烦，因此就只选择一个个体来进行自我繁衍。过程中需要记录全局最优、当前最优，然后随机一个排列，交换部分元素并更新答案即可。有人会说我还是过不了，跑得太慢了。那是因为做了很多无用的交换，我们枚举交换的位置，然后依次检查对答案的贡献是否为正。只要当前序列还能继续创造更优解，那么让它进行下去，否则对序列进行一次大清洗，从头来过。

这里只放遗传算法的代码：

#include <bits/stdc++.h>
#define N 1010
#define PRINT_TABLE
#define LIMIT 141473199965824ll // 每个测试点的最大值

#pragma optimize(3)

using namespace std;

typedef long long ll;

int n;
ll ans = 0, submax = 0;
random_device rd;
ll a[N], p[N], q[N], id[N];

ll calc(const ll arr[] = p) {
    ll sum = arr[1] * a[arr[n]] * a[arr[1]] * a[arr[2]];
    for (int i = 2; i < n; i++) sum += arr[i] * a[arr[i - 1]] * a[arr[i]] * a[arr[i + 1]];
    sum += arr[n] * a[arr[n - 1]] * a[arr[n]] * a[arr[1]];
    return sum;
}

ll d(int pos1, int pos2) {
    ll sum = 0;
    sum -= p[pos1] * a[p[pos1 - 1]] * a[p[pos1]] * a[p[pos1 + 1]] + p[pos1 + 1] * a[p[pos1]] * a[p[pos1 + 1]] * a[p[pos1 + 2]] + p[pos1 - 1] * a[p[pos1 - 2]] * a[p[pos1 - 1]] * a[p[pos1]];
    sum -= p[pos2] * a[p[pos2 - 1]] * a[p[pos2]] * a[p[pos2 + 1]] + p[pos2 + 1] * a[p[pos2]] * a[p[pos2 + 1]] * a[p[pos2 + 2]] + p[pos2 - 1] * a[p[pos2 - 2]] * a[p[pos2 - 1]] * a[p[pos2]];
    swap(p[pos1], p[pos2]);
    sum += p[pos1] * a[p[pos1 - 1]] * a[p[pos1]] * a[p[pos1 + 1]] + p[pos1 + 1] * a[p[pos1]] * a[p[pos1 + 1]] * a[p[pos1 + 2]] + p[pos1 - 1] * a[p[pos1 - 2]] * a[p[pos1 - 1]] * a[p[pos1]];
    sum += p[pos2] * a[p[pos2 - 1]] * a[p[pos2]] * a[p[pos2 + 1]] + p[pos2 + 1] * a[p[pos2]] * a[p[pos2 + 1]] * a[p[pos2 + 2]] + p[pos2 - 1] * a[p[pos2 - 2]] * a[p[pos2 - 1]] * a[p[pos2]];
    return sum;
}

int rand(int l, int r) {
    return (int) (rd() % (r - l + 1)) + l;
}

void GA() {
    while (ans < LIMIT) {
        for (int i = 1; i <= 20; i++) {
            int a = rand(1, n), b = rand(1, n);
            swap(p[a], p[b]);
        }
        submax = calc(); // 当前值
        shuffle(id + 1, id + 1 + n, mt19937(rd())); // 每次打乱枚举顺序
        clog << "Reset..." << endl;
        bool flag;
        do { // 还能变得更优就继续下去
            flag = false;
            for (int i = 1; i < n; i++) {
                for (int j = i + 1; j <= n; j++) {
                    ll cur;
                    int pos1 = id[i], pos2 = id[j];
                    if (abs(pos2 - pos1) <= 5 || abs(pos2 - pos1) >= n - 5) {
                        swap(p[pos1], p[pos2]);
                        cur = calc();
                    } else {
                        cur = submax + d(pos1, pos2);
                    }
                    if (cur > ans) {
                        ans = submax = cur;
                        memcpy(q, p, sizeof p);
                        if (ans > (ll) (LIMIT * 0.999)) cerr << ans << endl;
                        flag = true;
                        if (ans >= LIMIT) return;
                    } else if (cur > submax) {
                        submax = cur;
                        flag = true;
                    } else swap(p[pos1], p[pos2]);
                }
            }
        } while (flag);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    // Test Point #4 #5 #6 #7 #8 #9
    freopen("9.in", "r", stdin);
    freopen("9.out", "w", stdout);
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    for (int i = 1; i <= n; i++) p[i] = i, id[i] = i;
    GA();
    clog << "Final Answer: " << calc(q) << " Overloaded: " << calc(q) - LIMIT << endl;
#ifdef PRINT_TABLE
    cout << '{';
    for (int i = 1; i < n; i++) cout << q[i] << ", ";
    cout << q[n] << "}\n";
#else
    for (int i = 1; i <= n; i++) cout << q[i] << ' ';
#endif
    return 0;
}