引入
如果说数论是数学体系中专门用来研究数字性质的一个分支,那么初等数论则是对整数的性质进行系统性的探讨与研究。千万不要因为其中的“初等”二字小瞧这初等数论尽管名称和学习难度上都没有高等数论那么有逼格,就像初等数学之于高数,数论的所有内容均筑基于此。其中欧几里得证明的算数基本定理(一切合数都可被分解为有限个质数的乘积)在质数筛、GCD(以及LCA)计算、无理数证明等问题上均有用武之地。可以说高等数论奠基于初等数论。它同时也是初学者接触数论的必经之路。
Part1. 前置知识
Div1. 数论有关定理
算术基本定理 :每一个合数都可以被分解为有限个质数的乘积。即对于任意合数
推论一 :正整数
推论二 :正整数
推论三 :正整数
质数分布定理 :区间
费马小定理: 若
欧拉定理(费马小定理扩展): 若
Div2. 同余
同余 ,顾名思义,两个数分别除以一个正整数“对于正整数 。当然以上两种说法是等价的。
同余具有以下三种基本性质:
反身性:对于任何正整数
对称性:即对于
传递性:若
当然,它可以延申到计算机的模运算(毕竟出现了
加运算:
减运算:
乘运算:
还有两个推论:
幂运算:
求和运算:
同余消去原则:
若同余号两端的项相等,且都与模
举例:
Part2. 质数
质数的判断:除了它自身
Div1. 质数判断
试除法:
这是三种方法中,唯一一种能做到100%正确的质数判断方法 。对于给定数只能被1以及它本身整除 。
1 2 3 4 5 6 bool isPrime (int n) for (int i = 2 ; i * i <= n; i++) { if (n % i == 0 ) return false ; } return true ; }
复杂度:
适用范围:普及、提高
试除法の大胜利!
费马素性检验:
是上述费马小定理的实际运用,它与常规算法思想有所不同:它主张在费马伪素数 ,因为它很大概率 是一个质数。
1 2 3 4 5 6 7 8 9 10 11 bool isPrime (int n) if (n <= 2 ) return false ; int k = 10 ; while (k--) { srand (time (0 )); int a = rand () % (n - 2 ) + 2 ; if (__gcd(a, n) != 1 ) return false ; if (qpow (a, n - 1 , n) != 1 ) return false ; } return true ; }
复杂度:
适用范围:提高T2及以下(慎用)
为什么用该方法判断的质数 大概率
是个质数呢?不妨测试一下561(3)、1105(5)、1729(7)(括号内为它的最小因子),你会发现函数的返回值均为true,即都为质数。可见这个算法不是100%正确的,这些“漏网之鱼”被称为“Carmichael数”。它们极其罕见,一亿范围内仅255个。也因如此,你可以通过打表特判的方式抠掉这些特例(你保证记得住就行)。2016年中国物流工人余建春给出了一个Carmichael数的判断准则,这个标准目前在国际上得到了广泛认同。
对于优化,你可以在函数起始点加入类似于if (n % 2 == 0 || n % 3 == 0) return false;的特判,进一步降低复杂度。
Miller-Rabin算法:
该算法同样无法保证结果100%准确,慎用!
MB算法实质上是对费马素性检验算法的效率和准确度优化。算法流程如下:
将
从
计算
若结果不等于
若都不等于强费马证据 。
当然,它同样有特例,称为强伪质数 ,如2047(23)、3277(29)、4033(39)等(括号内为它的最小因子)。
Div2. 质数筛
常见的质数筛法有:试除法、埃氏筛、线性筛。
试除法 :从质数定义出发,即存在一个正整数
1 2 3 4 5 6 bool isPrime (int n) for (int i = 2 ; i * i <= n; i++) { if (n % i == 0 ) return false ; } return true ; }
复杂度:
适用范围:普及T2及以下
这里所展示的试除法代码实际上经过一轮优化。若严格根据质数定义,第二行的循环上限应为
埃氏筛 :全称叫埃拉托斯特尼筛法 ,老哥生活在2200年前的古希腊,不借助望远镜就计算出了地球的周长(与真实值偏差仅0.96%)、同时他也是第一位根据经纬线绘制出世界地图的人、也是最先提出将地球根据南北回归线分为“五带”的大人物。他提出的筛法核心思想如下:
第一步:列出从2开始的一列连续数字;第二步:选出第一个质数(本例中为2),将该质数标记,将数列中它的的所有倍数划去;第三步:若数列中的末项小于它前一项的平方,则质数已全部筛出;否则返回第二步 。
1 2 3 4 5 6 7 8 void get (int n) for (int i = 2 ; i <= n; i++) { if (!vis[i]) { prime[cnt++] = i; } for (int j = 2 ; i * j <= n; j ++) vis[i * j] = true ; } }
其中,prime数组存储质数,vis数组用于标记(即上文中“划去数字”),变量cnt则存储
复杂度:
适用范围:普及T2及以下
但是继续观察算法发现:我们其实无需将所有
这与前文介绍的埃氏法核心相符。因此将
1 2 3 4 5 6 7 8 void get (int n) for (int i = 2 ; i <= n; i++) { if (!vis[i]) { prime[cnt++] = i; for (int j = i + i; j <= n; j += i) vis[j] = true ; } } }
优化复杂度:
适用范围:普及T3及以下
线性筛/欧拉筛 :实质是埃氏筛的线性优化。因为在埃氏筛中,有些数字被重复筛了多次(例如30会被2、3、5筛到)。本着线性优化的原则,我们需要找到一个方法,使得每个合数仅被筛选一次。主要思想如下:
我们发现,线性筛和埃氏筛均使用了质数的 的结论。我们只需要保证每一个数仅被它自身的最小质因数筛出即可。即对于数字
1 2 3 4 5 6 7 8 9 void get (int n) for (int i = 2 ; i <= n; i++) { if (!vis[i]) prime[cnt++] = j; for (int j = 1 ; prime[j] <= n / i; j++) { vis[prime[j] * i] = true ; if (i % prime[j] == 0 ) break ; } } }
复杂度:
适用范围:普及、提高
例题:
P5736
【深基7.例2】质数筛 P5723
【深基4.例13】质数口袋
Part3. 因数
因数定义: 对于一个数
Div1. 因数分解法
试除法: 万能暴力解法。即遍历
1 2 3 4 5 6 7 8 9 10 11 12 vector<int > get (int n) { vector<int > ret; for (int i = 2 ; i * i <= n; i++) { if (n % i == 0 ) { ret.push_back (i); ret.push_back (n / i); } if (n % (i * i) == 0 ) ret.pop_back (); } sort (ret.begin (), ret.end ()); return ret; }
复杂度:
适用范围:普及T1
Div2.最大公约数
辗转相除法:
又是我们大名鼎鼎的欧几里得老先生提出的一套公约数算法,整个算极其简洁:核心只有一行,即:
两个数的最大公约数等于其中较小的数字和二者之间余数的最大公约数
可以写出:
1 2 3 int gcd (int a, int b) return b ? gcd (a, a % b) : a; }
但是为什么
假设如下关系:
首先证明充分性:令
代入初始除法算式得:
接着由于加减乘法的封闭性,即一个整数进行加减乘运算得到的结果同样是一个整数。可以得出:
接下来证必要性。令
Stein算法:
上一个方法的明显缺点在于,它处理大质数的效率并不好(但总体来说是很好的),因为它使用了取余运算,这会减慢一些速度。可以理解,生在2000多年前——一个没有电脑和OI的古希腊社会,这个算法已经足够兼顾常规效率和手推难度了。但是步入21世纪,加快的生活节奏毒瘤数据使得人们对更快算法的需求空前高涨。Stein算法便应运而生。
算法流程如下:
任意给定两个正整数,先判断它们是否都是偶数,若是,则用2约简,若不是,则执行第二步。
若两数是一奇一偶,则偶数除以2,直至两数都成为奇数。再以较大的数减较小的数,接着取所得的差与较小的数,若两数一奇一偶,仍然偶数除以2,直至两数都成为奇数。再次以大数减小数。不断重复这个操作,直到所得的减数和差相等为止。
两数相等时,第一步中约掉的若干个2与第二步中最终的等数的乘积就是所求的最大公约数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 int gcd (int a, int b) int p = 0 , t; if (!(1 & a) && !(1 & b)) { a >>= 1 ; b >>= 1 ; p++; } while (!(1 & a)) a >>= 1 ; while (!(1 & b)) b >>= 1 ; if (a < b) { t = a; a = b; b = t; } while (a = ((a - b) >> 1 )) { while (!(1 & a)) a >>= 1 ; if (a < b) { t = a; a = b; b = t; } } return b << p; }
这个算法的优点在于:它大大优化了大质数的运算。但可惜的是,它的代码量膨胀了8倍,因此不太建议赛时使用。毕竟C++都给你内置了__gcd()函数嘛,干嘛不偷个懒?
Div3. 最小公倍数
我们可以简单概括成一句话:
两个数的最小公倍数等于这两个数的乘积与这两个数最大公约数的商
即:
凭啥呀?
我们假设两个数
由乘法交换律,可知:
消去
例题:
P1075 [NOIP2012
普及组] 质因数分解 P2424 约数和
(需要逆向思维)
Part4. 欧拉函数相关
Div1. 欧拉函数推导
问:论牧师欧拉有多么的高产
答:平均每年800页数学论文你说高不高产嘛
欧拉函数 ,记作
欧拉函数有如下计算公式:若
推导思想即为用 。在计算机上实现,首先需要分解质因数。思路如下:首先抛出第一个质因数否则他们将存在最大公约数 。那么能被
因此我们离解出欧拉函数就进了一步了,我们的过渡式子就是
好耶
别急着好耶,我们可以发现一个小小的推导谬误(可能并不是很容易发现)。当我们用
容斥原理
易知因为 。因此需要补偿损失,正确的计算方法是(仅计算能被
能被
能被
同时被
总个数:
那么对于
回到欧拉函数推导上来:过渡公式对于可同时被两个不同质数整除的数(例如
得到
当然这又有一个小问题没完没了了是不是?:对于 。还是回到上图:中间的括号外有减号需要变号 ,不要忘记相减 得来的)。得到我们的过渡态3:
又是如上的容斥判断,这里我们省去讨论。将最终的产物合并得到:
终于可以好耶了……
Div2. 欧拉函数代码实现
主要是如果压成一个Div会非常的长,因此这里新开一个Div2
我们明确了欧拉函数的推导,接下来就是整理思路写代码的时间了!我们也只需跟着原始思路走就可以了。再次回忆一下:首先我们需要筛出质因数,除去它的所有倍数,再用公式
1 2 3 4 5 6 7 8 9 10 11 long long eular (int n) long long res = n; for (int i = 2 ; i * i <= n; i++) { if (n % i == 0 ) { res = res * (i - 1 ) / i; while (n % i == 0 ) n /= i; } } if (n > 1 ) res = res * (n - 1 ) / n; return res; }
时间复杂度:
适用范围:All Clear
Div3. 欧拉函数推论
若
让我们回到欧拉函数的定义上去:
很显然,答案是
假设
凭啥呀?
因为
那么函数值多乘了一个
我们发现:(2)式中包含了(1)式,只是头上乘以了
假设
这东西长得和性质2很相似,唯一不同的是
因为
这三个性质将作为重点性质出现在欧拉函数筛法中。
Div4. 欧拉函数线性筛
我们已经接触了简单的欧拉函数计算方法,那么又该如何解决形如:“给定一个正整数
考虑继续使用上面的朴素算法,时间复杂度将会是
欧拉函数涉及到质因子的拆分,我们又需要在线性时间内求各种质数。自然而然想到了先前所学的线性筛:
1 2 3 4 5 6 7 8 9 10 11 12 13 int primes[N];bool st[N];int cnt = 0 ;void sieve (int n) for (int i = 2 ; i <= n; i++) { if (!st[i]) primes[++cnt] = i; for (int j = 1 ; primes[j] * i <= n; j++) { st[primes[j] * i] = true ; if (i % primes[j] == 0 ) break ; } } }
我们运用这段代码可以得出st[N]数组可以筛出所有的合数。也就是说对于筛出的合数,我们能够得知组成它的质因子是什么,比如st[primes[j]*i]=true;这一行代码。接着套用上述三种性质,我们可以得出
此时我们就需要新建一个phi[N]数组来存储每个数的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 typedef long long ll;ll primes[N]; bool st[N];int cnt = 0 ;ll phi[N]; void phi_sieve (int n) for (int i = 2 ; i <= n; i++) { if (!st[i]) { primes[++cnt] = i; phi[i] = i - 1 ; } for (int j = 1 ; primes[j] * i <= n; j++) { st[primes[j] * i] = true ; if (i % primes[j] == 0 ) { phi[primes[j] * i] = phi[i] * primes[j]; break ; } phi[primes[j] * i] = phi[i] * (primes[j] - 1 ); } } }
没错我开了long long防止爆int
时间复杂度:
适用范围:普及&提高
对于开头提出的求和问题,遍历phi[1]到phi[n]的所有值求和即可。
Div5. 欧拉定理
若正整数
对于它的证明,百度百科 中如此写到:
取
通俗来讲就是这样:
在
给这列数同时乘上
提出括号里乘了
那么根据同余号两端的消去原则(左右两端两个项相同且与模
特殊地,如果
真不知道明明可以写得通俗点为什么非得省那点空间写看起来那么高深莫测的专业术语,真的是只写给自己看的。
Div6. 降幂算法
尤其对于绿题以上的题目,题面中可能出现“答案可能很大,请对大质数 ”的字样。这意味着题目可能涉及到大规模的幂运算,需要我们用简便的方法计算幂。对于一般的题目,我们使用快速幂。
快速幂 :快速幂思想如下:
我们将指数
1 2 3 4 5 6 7 8 9 10 11 typedef long long ll;int qpow (int a, int k, int p) int res = 1 ; while (k) { if (k & 1 ) res = (ll) res * a % p; a = a * a % p; k >>= 1 ; } return res; }
时间复杂度:
适用范围:基本All Clear
欧拉降幂 :上面方法一个缺点在于无法处理过大的指数,在处理类似于
欧拉降幂核心公式:扩展欧拉定理 )
也就是说:我们只需要算出long long,因此可以选择使用字符串进行高精度计算。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 typedef long long ll;ll primes[N]; bool st[N];int cnt = 0 ;int qpow (int a, int k, int p) int res = 1 ; while (k) { if (k & 1 ) res = (ll) res * a % p; a = a * a % p; k >>= 1 ; } return res; } ll eular (int n) { ll res = 0 ; for (int i = 2 ; i <= n; i++) { if (!st[i]) { primes[++cnt] = i; res = res * (i - 1 ) / i; while (n % i == 0 ) n /= i; } for (int j = 1 ; i * primes[j] <= n; j++) { st[i * primes[j]] = true ; if (i % primes[j] == 0 ) break ; } } if (n > 1 ) res = res * (n - 1 ) / n; return res; } int edp (int a, string k, int p) ll phi = eular (p); int drop = 0 ; for (int i = 0 ; i < k.length (); i++) { drop *= 10 ; drop += k[i] % phi; } drop += phi; return qpow (a, drop, p); }
其中eular(int n)函数用于计算欧拉函数的值、edp(int a, string k, int p)用于计算降幂后的指数、qpow(int a, int k, int p)是快速幂算法。
时间复杂度:
适用范围:所有
扩展欧拉定理可谓是欧拉定理的一般形式,它的定义如下:对于任意正整数
$ak\begin{cases}a k&(;p
),gcd(a,p),k<(p)\a{k(p)+(p)}&(;p),gcd(a,p),k(p) {k(p)}&(;p),gcd(a,p)=1\end{cases}
$
其中第二个式子就是欧拉降幂的核心公式。
扩展欧拉定理的证明见这里 。因为太复杂了我不会证
例题:
P2158 [SDOI2008]
仪仗队 (欧拉函数板子)P1447 [NOI2010]
能量采集 (上一个问题的变式)P1226 [模板]
快速幂 P5091 [模板]
扩展欧拉定理 (欧拉降幂)P4139
上帝与集合的正确用法 (欧拉降幂+递归)
Part5. 同余方程的解法
这里会涉及到一元线性同余方程,一元线性同余方程组和高次同余方程的算法解法。
Div.1 裴蜀定理
很多人会把他读成裴除(chú)(比如我的某位好友),这个名词正确的读法是裴蜀(shǔ) 。或者可以直接改称作“贝祖定理”,它的提出者艾蒂安·裴蜀估计怎么也没想到后人居然连他的名字都读不对(想想如果这种事情发生到你身上会怎么样)。你也可以读他名字的法语发音
切入正题,裴蜀定理表述为:对于任意正整数 ,其中
首先可以知道
Div2. 扩展欧几里得(EXGCD)
加了“扩展”二字是不是感觉逼格上来了?
扩展欧几里得算法用于求出线性同余方程的解。线性同余方程,即形如
回忆一下欧几里得算法的核心思路:
再看看刚刚讲到的裴蜀定理,发现
那么我们的任务就是求出这里的
既然我们设计的是一个递归算法,我们就必须明确它的递归出口。根据欧几里得算法,当
最后,因为这本质上还是一个欧几里得算法,所以返回
1 2 3 4 5 6 7 8 9 10 int exgcd (int a, int b, int &x, int &y) if (!b) { x = 1 ; y = 0 ; return a; } int d = exgcd (b, a % b, y, x); y -= a / b * x; return d; }
时间复杂度:
但是,题目中一般不会给出裴蜀定理那样的形式,而是形如正整数解 呢?接下来就是解决上述问题的方法:
1. 同余—等式互转 (自己起的名字):
在上面的介绍中,我们遇到了一个问题:如何将
考虑到同余方程的定义(或者你可以把以下关系死记住),得到exgcd求解
2. 最值解问题 :
二元一次不定方程通解的证明
Div3. 中国剩余定理(CRT)
又称孙子定理(但我认为还是中国剩余定理听起来更有实力一些),最早见于《孙子算经》中“物不知数”问题,首次提出了有关一元线性同余方程的问题与解法。
对于一元线性同余方程:
首先,令
然后,令
接着,令
所以,
Div4. Baby Step Giant
Step算法(BSGS)
这个算法用于解决一元高次同余方程问题,模意义下的对数也可以求。又称“北上广深算法”(想出这种名字的人真是人才)。
高次同余方程长成这个样子:
发现真是变态呢。这种问题显然没公式解,于是苦恼的人们只得选择一条略显暴力的求解道路,即搜索 。严格来说,BSGS所使用的是双搜索,其中的一个变量的搜索步长会长于另一个变量的搜索步长,因而得名“大步小步算法”。或者叫北上广深/拔山盖世算法!
朴素BSGS (
接下来我们对同余号右侧的部分求值,再任命一个固定的
关于哈希表冲突,我们希望找到
对于
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 ll bsgs (ll a, ll b, ll m) { unordered_map<ll, ll> hash; ll bs = 1 ; int t = sqrt (m) + 1 ; for (int B = 1 ; B <= t; B++) { bs *= a; bs %= m; hash[b * bs % m] = B; } ll gs = bs; for (int A = 1 ; A <= t; A++) { auto iter = hash.find (gs); if (iter != hash.end ()) return A * t - it->second; gs *= bs; gs %= m; } return -1 ; }
时间复杂度:
扩展BSGS (
例题:
P1082 [NOIP2012
提高组] 同余方程 (exgcd)P5656 [模板]
二元一次不定方程 (exgcd) P1495 [模板]
中国剩余定理(CRT)/ 曹冲养猪 P1516
青蛙的约会 (CRT+exgcd)P3846 [TJOI2007]
可爱的质数/ [模板] BSGS P2485 [SDOI2011]
计算器 (欧拉降幂+乘法逆元+BSGS)P3306 [SDOI2013]
随机数生成器 (等比数列推导+BSGS)P4195 [模板] 扩展
BSGS/exBSGS
Part6. 乘法逆元
乘法逆元定义如下(注意和矩阵求逆不是一个东西):
若
简单来说乘法逆元
费马小定理求逆元 :大部分题目会给出一个质数模数,因而互质是可以保证的。此时我们的乘法逆元就是使式子
得到
1 2 3 int inv (int a, int p) return qpow (a, p - 2 , p); }
扩展欧几里得求逆元 :这是万能的方法,对任意模数均成立。它不像上面费马小定理那样限制模数必须是质数,因而只要时间充裕,都建议使用这种求逆元的方式。
因为exgcd的形式。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 int exgcd (int a, int b, int &x, int &y) if (!b) { x = 1 ; y = 0 ; return a; } int d = exgcd (b, a % b, y, x); y -= a / b * x; return d; } int inv (int a, int m) int x, y; exgcd (a, m, x, y); return (x + m) % m; }
递推求逆元 :
例题:
P3811 [模板]
模意义下的乘法逆元 (递推求逆元)
来张弔图
Part7. 矩阵相关
矩阵,是一个按照长方排列的实数或复数集合。它最早用来表示方程组中的系数和常数,简单理解就是它将
Div1. 初等行变换
考虑这个方程组:
按照如上所述,将它转换为系数矩阵(只有
你也可以写成增广矩阵(与系数矩阵相比多了一列常数,即等号右边的常数,这里用竖线隔开)的形式:
不难看出第一列代表了
交换某两行
把矩阵的某一行同乘以一个非零的数
把某行的若干倍加和到另一行
假设我们有一个三角矩阵 的概念:
顾名思义,系数排列看起来像一个三角形的矩阵,叫做三角矩阵。分为上三角矩阵和下三角矩阵。前者的非零系数均分布在对角线的右上方、后者都在左下方,例如矩阵:
那么如何将一个一般矩阵转换为上三角矩阵呢?答案是前面介绍过的初等行变换!步骤如下:
枚举每一列
通过加减有序组中某一行的非零倍,将之后所有行的第
文字还是太抽象,我们来举个例子:
令矩阵
枚举第一列,
第二步,自乘并标记有序,因此第一行除以
第三步,将无序组的第
枚举第二列,此时
最终的最终,第三行减
我们假设从左到右,分别为
根据最后一行,显然
然而心细的你估计发现了疏漏之处:“求一元二次方程时都要先检验根是否存在(
事实上,矩阵的解的分布确实不止一种情况,这里是矩阵有唯一解的情况。类比高中立体几何求平面法向量的情景,我们通常都要令某个坐标为秩 的概念。
Div2. 秩
在上一节中我们通过初等行变换求出了矩阵的解,然而并不是所有矩阵都能轻而易举求出唯一解,因为它可能无解、也有可能无唯一解(默认最高次数为一)。类比一元二次方程中的
答案是:有滴!在矩阵运算中,我们使用秩 来描述矩阵的一些关于解的个数的关系。秩被定义为:将矩阵通过初等行变换后形成的梯形矩阵中非零行的个数。试看如下例子:
定义一个
经过初等行变换后出现了这样的情况:
第二行变成了纯
它有无数组解,原因是:矩阵的秩与矩阵增广矩阵的秩相等且小于了它的阶 。简单来说就是你用两个方程去求三个未知数的值(初一内容),当然是有无数多组解。
规定对于矩阵
看第二个例子:
定义增广矩阵:
增广矩阵变换后:
根据定义,得到
加上第一节里面的结论,我们总结出了矩阵解分布的三种情况(方程组的增广矩阵为
当
当
当
因此就有了一套组合算法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 #include <bits/stdc++.h> #define N 110 #define NO_SOLUTION -1 #define INFINITE 0 #define SOLVE_OK 1 using namespace std;typedef long long ll;double mat[N][N];int n;double eps = 1e-6 ; int solve () int rank = 0 ; for (int c = 0 , r = 0 ; c < n; c++) { int t = r; for (int i = r; i < n; i++) { if (fabs (mat[i][c]) > fabs (mat[t][c])) t = i; } if (fabs (mat[t][c]) < eps) continue ; for (int i = c; i <= n; i++) swap (mat[r][i], mat[t][i]); for (int i = n; i >= c; i--) mat[r][i] /= mat[r][c]; for (int i = r + 1 ; i < n; i++) { if (fabs (mat[i][c]) > eps) { for (int j = n; j >= c; j--) { mat[i][j] -= (mat[r][j] * mat[i][c]); } } } r++; rank = r; } if (rank < n) { for (int i = rank; i < n; i++) { for (int j = 0 ; j < n + 1 ; j++) { if (fabs (mat[i][j]) > eps) return NO_SOLUTION; } } return INFINITE; } for (int i = n - 1 ; i >= 0 ; i--) { for (int j = i + 1 ; j < n; j++) { mat[i][n] -= mat[i][j] * mat[j][n]; } } return SOLVE_OK; } int main () cin>>n; for (int i = 0 ; i < n; i++) { for (int j = 0 ; j < n + 1 ; j++) cin>>mat[i][j]; } int res = solve (); if (res != SOLVE_OK) cout<<res<<endl; else for (int i = 0 ; i < n; i++) { if (fabs (mat[i][n]) < eps) mat[i][n] = fabs (mat[i][n]); printf ("x%d=%.2lf\n" , i + 1 , mat[i][n]); } return 0 ; }
时间复杂度:
以后上大学解高次线性方程就可以用这段程序秒了。
Div3. 矩阵基本运算
1. 加法 :
注意类比只有同型的矩阵才有加法运算 (同型即行数列数相等)。
可以知道,四则运算的加法交换律和结合律仍然适用于矩阵加法。
2. 减法 :
加法的逆运算,让矩阵同一位置的元素相减即可。也是仅限于同型矩阵之间才可做减法。
3. 数乘 :
即矩阵中每个元素都跟数字相乘。符合乘法交换律和结合律
矩阵的加法、减法和数乘合称为矩阵的线性运算
4. 转置 :
矩阵
直观来讲就是将原矩阵旋转一下(行和列互换)。满足如下性质:
5. 共轭 :
矩阵
类比共轭复数的定义:实部不变、虚部取相反数。矩阵共轭变换就是将矩阵中的所有复数变为其共轭形式。
6. 共轭转置 :
矩阵
字面意思,先取共轭,再转置。它具备转置矩阵的三条性质。
Div4. 矩阵乘法
只有一个矩阵的行数和另一个矩阵的列数相等时才可进行乘法运算 。
例如一个
因此
它满足结合律、分配律,但是大多数情况下不满足交换律。交换律不成立可以看到下面这个例子:
首先根据定义,
对于结果是正方形矩阵的,可以自己随便设置两个矩阵进行计算。但是部分矩阵仍然可以进行交换律运算:矩阵乘一个单位矩阵/数量矩阵[
Div5. 其他常用类型的矩阵
1. 零矩阵 :顾名思义,由
2. 单位矩阵 :形如
3. 数量矩阵 :形如
4. 逆矩阵 :如果存在一个矩阵
5.
对称矩阵 :转置矩阵与自身相等的矩阵叫做对称矩阵,特征是所有元素关于对角线对称,例如:
Div6. 矩阵的几何表示
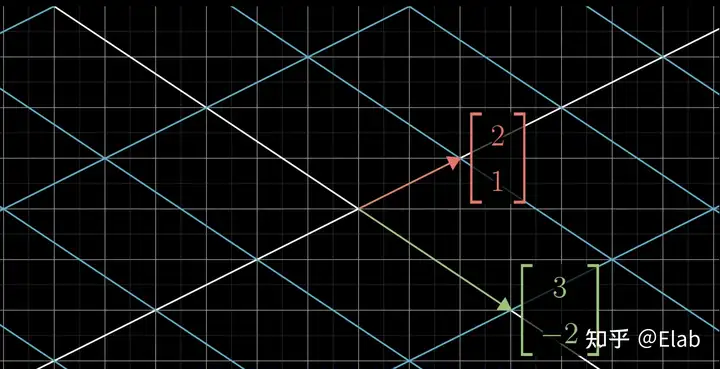
平面直角坐标系上,一个向量
计算机中,用两个不共线向量
假设我们常规想法中的平面直角坐标系是
如果在最开始的坐标系中有一个向量
抽象之后变成:
例题:
P3389 [模板]
高斯消元法 (上三角矩阵的转换)P2455 [SDOI2006]
线性方程组 (前一道题的升级版)
Part8. 组合计数
StarterDiv1. 阶乘概述
阶乘,数学中用
特殊地,
StarterDiv2. 常用排列总结
1. 排列数 :数学中用
为啥呢?,有弔图为证↓
2. 组合数 :假设有乌鸦坐飞机
弔图×2↓
GZ表示就凭这几张图他能速通整个组合数的内容
StarterDiv3. 二项式定理
学过初中的大家都知道:
二项式定理定义式如下:
这里出现的但是这一章并不会用它,只是作补充知识的说……
有这三条就够了,接下来进入组合计数的内容。
Div1. 高考娃狂喜——组合数计算
一个小栗子:
宇宙榜一大学阿福大学的榜一博士后导师黑虎阿福给你出了一道难题:
给你两个正整数
你 :“这还不简单?”
阿福 : “好的,我这里将
你 : “WTF?”
于是你决定用程序来代替人脑,阿福教授也做出了一定让步,让你求出而不是妄想着用2077年的赛博机器运行暴力计算,来解决这个问题。
一旦你的运行时间超过一秒,阿福教授就会使用战技“乌鸦坐飞机”对你造成大量阶乘伤害。已经学习了阶乘的你想必已了解了它的威力,所以还是老老实实推导公式吧!
递推版:
组合数递推公式:
分析思路类似于动态规划问题:我们要从
上图中,若包含这个红色物体,那么我们只需再从剩下的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 #include <bits/stdc++.h> #define N 2010 using namespace std;int c[N][N];void Csieve (int p) for (int i = 0 ; i < N; i++) { for (int j = 0 ; j <= i; j++) { if (!j) c[i][j] = 1 ; else c[i][j] = (c[i - 1 ][j - 1 ] + c[i - 1 ][j]) % p; } } } int main () int a, b, p; cin>>a>>b>>p; Csieve (p); cout<<c[a][b]<<endl; return 0 ; }
时间复杂度:
适用于
预处理版:
但是众所周知,递归有两大痛点:对于主观思维来说,是边界问题;对于客观条件来说,是内存。递归过程中CPU里储存了大量的未运行或者待返回的函数实例,当
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 #include <bits/stdc++.h> #define N 100010 using namespace std;typedef long long ll;int fact[N], infact[N];int qpow (int a, int b, int p) int res = 1 ; while (b) { if (b & 1 ) res = (ll) res * a % p; a = (ll) a * a % p; b >>= 1 ; } return res; } int inv (int a, int p) return qpow (a, p - 2 , p); } int C (int a, int b, int p) return ((fact[a] % p) * (infact[b] % p)) % p * infact[a - b] % p; } int main () int a, b, p; cin>>a>>b>>p; fact[0 ] = infact[0 ] = 1 ; for (int i = 1 ; i <= N; i++) { fact[i] = (ll) fact[i - 1 ] * i % p; infact[i] = (ll) infact[i - 1 ] * inv (i, p) % p; } cout<<C (a, b, p)<<endl; return 0 ; }
时间复杂度:
适用范围,int范围内的大部分情况。
Lucas定理优化版:
证明在此 (建议直接背结论)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 typedef long long ll;int p;int qpow (int a, int b) int res = 1 ; while (b) { if (b & 1 ) res = (ll) res * a % p; a = (ll) a * a % p; b >>= 1 ; } return res; } int inv (int a) return qpow (a, p - 2 ); } int C (int a, int b) int res = 1 ; for (int i = 1 , j = a; i <= b; i++, j--) { res = (ll) res * j % p; res = (ll) res * inv (i) % p; } return res; } ll lucas (int a, int b) { if (a < p && b < p) return C (a, b); return (ll) C (a % p, b % p) * lucas (a / p, b / p) % p; } int main () ios::sync_with_stdio (false ); cin.tie (0 ); cout.tie (0 ); int t; int n, m; cin>>t; while (t--) { cin>>n>>m>>p; cout<<lucas (n + m, n)<<endl; } return 0 ; }
时间复杂度:
其本质是套用
适用范围,long long范围内的大部分情况。
高精度版(选修):
什么?你厌倦了组合数后面挂着的模虽然前面几种也可以,毕竟手算的题数据很小取不取模都一样)是不是心动了呢?
常规思路来说,我们的组合数公式经过一轮分式化简可以得到:
我们看到了Part1 里面讲的算术基本定理,将组合数转化为
用它可以计算出
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 #include <bits/stdc++.h> #define N 10010 using namespace std;typedef long long ll;vector<int > num; ll primes[N], sum[N]; bool st[N];int cnt = 0 ;void prime_sieve (int n) for (int i = 2 ; i <= n; i++) { if (!st[i]) primes[++cnt] = i; for (int j = 1 ; i * primes[j] <= n; j++) { st[i * primes[j]] = true ; if (i % primes[j] == 0 ) break ; } } } int get (int a, int p) int res = 0 ; while (a) { res += a / p; a /= p; } return res; } vector<int > mul (vector<int > a, int b) { vector<int > res; int t = 0 ; for (int i = 0 ; i < a.size (); i++) { t += a[i] * b; res.push_back (t % 10 ); t /= 10 ; } while (t) { res.push_back (t % 10 ); t /= 10 ; } return res; } int main () int a, b; cin>>a>>b; prime_sieve (a); for (int i = 1 ; i <= cnt; i++) sum[i] = get (a, primes[i]) - get (b, primes[i]) - get (a - b, primes[i]); vector<int > res; res.push_back (1 ); for (int i = 1 ; i <= cnt; i++) { for (int j = 1 ; j <= sum[i]; j++) { res = mul (res, primes[i]); } } for (int i = res.size () - 1 ; i >= 0 ; i--) cout<<res[i]; cout<<endl; return 0 ; }
时间复杂度:
适用范围,int范围内。
有了这段代码,我们就可以完成开头阿福教授的原问题了(不模不限数据)!
Div2.
世界上最OI的IDE——Catalan数
当你翻开Catalan数的介绍文章,并大学特学了一番,感觉自己完全掌握了这神奇的数列,正当你兴致勃勃地打开题库搜索到一道Catalan数的题目正准备大展身手时,你会发现,面对这神奇的题干,不同于往常秒模板题的你,你甚至完全看不出来它和Catalan数有任何的关系,而且很有可能,你其实连Catalan数究竟是什么东西都不知道!
苏子愀然,正襟危坐而问客曰:“何为其然也?”
其实还真不能让那些博客背上黑锅,这种现象与Catalan数本身的应用有很大的关系。
Catalan数,或者习惯叫卡特兰数、明安图数,是组合数学中常用的特殊数列。数列如下:“
用最经典的例子写出来就是:
给你一个
假设你某时刻走到了点不合法的路径与直线 。用一张图来直观体会一下:
终点
那么如何来计算合法和不合法路径的条数呢?直接求出合法路径不好求,规律不好找,因此我们计算出总路径数量,减去不合法数量即是合法路径数量。
可以看到,无论选择什么样的路径,在不左移、不下移的前提下,到达
因为所有路径,包括合法的和不合法的路径都最终抵达了
(至于为什么用右移次数而不是上移次数,是因为上移受到限制,这意味着你可以一直右移到
扩展 :如果题干中指明向右走的次数不少于向上走的次数
那这些又和宇宙第一IDE有什么关系呢
应用场景一:括号匹配
将向右走转化为左括号“(”,向上走转化为右括号“)”。对于每一次输入,检查一下左括号输入次数是否永不小于右括号输入次数。若是,当输入最后一个右括号,使左右括号数量相同时,即为匹配成功;若不是,且左括号个数大于右括号个数,则表明括号等待补全;若不是,且左括号个数小于右括号个数,即立即宣布失配。
应用场景二:合法进出栈序列计数问题
假设一个初始为空的栈,有
答案就是Catalan数,自行套公式计算。
应用场景三:圆的不相交弦计数问题
假设一个圆周上分布着偶数个点,对这些点两两连线,使相连的线不相交的所有方案数。其中一个合法解如下图:
聪明如你,答案还是Catalan数!那么如何转化为已知问题求解呢?
我们将出发点标记为左括号“(”,从出发点引出去的线与其他线/点的所有交点标记为右括号“)”。当所有点两两连接完毕时,根据场景一的模型,一旦左右括号失配即代表不合法,否则合法。因此这个问题也就变成了:给定
例题:
P3807 [模板]
卢卡斯定理/Lucas 定理 P5014
水の三角(修改版) (Catalan数公式变形推导)