切线方程 & 切点弦方程# 该内容为后文部分二级结论证明过程中直接运用的前置结论,恳请读者首先阅读此章,了解切线方程和切点弦方程的求法和相关证明
切线方程是圆锥曲线中十分常用的附属结论,尽管它与圆锥曲线没有直接关系,但是它在设直线,尤其是证明蒙日圆、阿基米德三角形的相关结论时候有大用。可惜的是,该结论并不属于数学教材中推导并证明的定理,因此原则上不能在考场上不加证明地使用 。本章将对这两类方程的求法进行简要介绍和推导。
切线/切点弦方程的求法几乎相同,可以用“均分次数,均分系数”八个字概括。例如,我们要求椭圆/双曲线 E : x 2 a 2 ± y 2 b 2 = 1 E:\frac{x^2}{a^2}\pm\frac{y^2}{b^2}=1 E : a 2 x 2 ± b 2 y 2 = 1 P ( m , n ) P(m,n) P ( m , n )
均分次数:将 x 2 x^2 x 2 m m m y 2 y^2 y 2
做完后可以得到切线方程 l : m x a 2 + n y b 2 = 1 l:\frac{mx}{a^2}+\frac{ny}{b^2}=1 l : a 2 m x + b 2 n y = 1
如果是抛物线 y 2 = 2 p x y^2=2px y 2 = 2 p x
均分次数:同上,将 y 2 y^2 y 2 n y ny n y
均分系数:将一次项 2 p x 2px 2 p x p x + p x px+px p x + p x x x x
做完后可得切线方程 l : n y = p x + p m l:ny=px+pm l : n y = p x + p m
切线方程# 为什么上面讲到的八字真言会有效呢?接下来我们来证明切线方程。
评析 :可以有多种方法,其中一种是对圆锥曲线(隐函数)求导并代入得到切线方程;另外一种就是相当普通的解析几何方法。我们着重介绍后者,因为你可以毫无顾忌地把它呈现在你的解题过程中。
证明 :
设切点 P ( m , n ) P(m,n) P ( m , n )
现证椭圆的情况,双曲线同理(为节省篇幅不给出证明),设椭圆方程 E : x 2 a 2 + y 2 b 2 = 1 E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 E : a 2 x 2 + b 2 y 2 = 1 m 2 a 2 + n 2 b 2 = 1 \frac{m^2}{a^2}+\frac{n^2}{b^2}=1 a 2 m 2 + b 2 n 2 = 1
设切线 l : y − n = k ( x − m ) l:y-n=k(x-m) l : y − n = k ( x − m ) y = k x − m k + n y=kx-mk+n y = k x − mk + n
{ y = k x − m k + n x 2 a 2 + y 2 b 2 = 1 \begin{cases}
y=kx-mk+n
\\\frac{x^2}{a^2}+\frac{y^2}{b^2}=1
\end{cases} { y = k x − mk + n a 2 x 2 + b 2 y 2 = 1 得:
b 2 x 2 + a 2 ( k 2 x 2 + m 2 k 2 + n 2 − 2 m k 2 x + 2 n k x − 2 m n k ) − a 2 b 2 = 0 b 2 x 2 + a 2 k 2 x 2 + a 2 m 2 k 2 + a 2 n 2 − 2 m a 2 k 2 x + 2 a 2 n k x − 2 a 2 m n k − a 2 b 2 = 0 ( b 2 + a 2 k 2 ) x 2 + ( 2 a 2 n k − 2 m a 2 k 2 ) x + a 2 m 2 k 2 + a 2 n 2 − 2 a 2 m n k − a 2 b 2 = 0 Δ = 0 ( 2 a 2 n k − 2 m a 2 k 2 ) 2 − 4 ( b 2 + a 2 k 2 ) ( a 2 m 2 k 2 + a 2 n 2 − 2 a 2 m n k − a 2 b 2 ) = 0 4 a 4 n 2 k 2 + 4 m 2 a 4 k 4 − 8 m n a 4 k 3 − 4 a 2 b 2 m 2 k 2 − 4 a 2 b 2 n 2 + 8 a 2 b 2 m n k + 4 a 2 b 4 − 4 m 2 a 4 k 4 − 4 a 4 n 2 k 2 + 8 a 4 m n k 3 + 4 a 4 b 2 k 2 = 0 − 4 a 2 b 2 m 2 k 2 − 4 a 2 b 2 n 2 + 8 a 2 b 2 m n k + 4 a 2 b 4 + 4 a 4 b 2 k 2 = 0 − 4 m 2 k 2 − 4 n 2 + 8 m n k + 4 b 2 + 4 a 2 k 2 = 0 − m 2 k 2 − n 2 + 2 m n k + b 2 + a 2 k 2 = 0 ( a 2 − m 2 ) k 2 + 2 m n k + b 2 − n 2 = 0 ( a 2 − m 2 ) k 2 + 2 m n k + a 2 n 2 a 2 − m 2 − n 2 = 0 ( a 2 − m 2 ) k 2 + 2 m n k + m 2 n 2 a 2 − m 2 = 0 a 2 n 2 b 2 k 2 + 2 m n k + b 2 m 2 a 2 = 0 ( a n b k + b m a ) 2 = 0 k = − b 2 m a 2 n \begin{aligned}
\\b^2x^2+a^2(k^2x^2+m^2k^2+n^2-2mk^2x+2nkx-2mnk)-a^2b^2&=0
\\b^2x^2+a^2k^2x^2+a^2m^2k^2+a^2n^2-2ma^2k^2x+2a^2nkx-2a^2mnk-a^2b^2&= 0
\\(b^2+a^2k^2)x^2+(2a^2nk-2ma^2k^2)x+a^2m^2k^2+a^2n^2-2a^2mnk-a^2b^2&=0
\\\Delta&=0
\\(2a^2nk-2ma^2k^2)^2-4(b^2+a^2k^2)(a^2m^2k^2+a^2n^2-2a^2mnk-a^2b^2)&=0
\\\cancel{4a^4n^2k^2}+\cancel{4m^2a^4k^4}-\cancel{8mna^4k^3}-4a^2b^2m^2k^2-4a^2b^2n^2+8a^2b^2mnk+4a^2b^4-\cancel{4m^2a^4k^4}-\cancel{4a^4n^2k^2}+\cancel{8a^4mnk^3}+4a^4b^2k^2&=0
\\-4a^2b^2m^2k^2-4a^2b^2n^2+8a^2b^2mnk+4a^2b^4+4a^4b^2k^2&=0
\\-4m^2k^2-4n^2+8mnk+4b^2+4a^2k^2&=0
\\-m^2k^2-n^2+2mnk+b^2+a^2k^2&=0
\\(a^2-m^2)k^2+2mnk+b^2-n^2&=0
\\(a^2-m^2)k^2+2mnk+\frac{a^2n^2}{a^2-m^2}-n^2&=0
\\(a^2-m^2)k^2+2mnk+\frac{m^2n^2}{a^2-m^2}&=0
\\\frac{a^2n^2}{b^2}k^2+2mnk+\frac{b^2m^2}{a^2}&=0
\\\left(\frac{an}{b}k+\frac{bm}{a}\right)^2&=0
\\k&=-\frac{b^2m}{a^2n}
\end{aligned} b 2 x 2 + a 2 ( k 2 x 2 + m 2 k 2 + n 2 − 2 m k 2 x + 2 nk x − 2 mnk ) − a 2 b 2 b 2 x 2 + a 2 k 2 x 2 + a 2 m 2 k 2 + a 2 n 2 − 2 m a 2 k 2 x + 2 a 2 nk x − 2 a 2 mnk − a 2 b 2 ( b 2 + a 2 k 2 ) x 2 + ( 2 a 2 nk − 2 m a 2 k 2 ) x + a 2 m 2 k 2 + a 2 n 2 − 2 a 2 mnk − a 2 b 2 Δ ( 2 a 2 nk − 2 m a 2 k 2 ) 2 − 4 ( b 2 + a 2 k 2 ) ( a 2 m 2 k 2 + a 2 n 2 − 2 a 2 mnk − a 2 b 2 ) 4 a 4 n 2 k 2 + 4 m 2 a 4 k 4 − 8 mn a 4 k 3 − 4 a 2 b 2 m 2 k 2 − 4 a 2 b 2 n 2 + 8 a 2 b 2 mnk + 4 a 2 b 4 − 4 m 2 a 4 k 4 − 4 a 4 n 2 k 2 + 8 a 4 mn k 3 + 4 a 4 b 2 k 2 − 4 a 2 b 2 m 2 k 2 − 4 a 2 b 2 n 2 + 8 a 2 b 2 mnk + 4 a 2 b 4 + 4 a 4 b 2 k 2 − 4 m 2 k 2 − 4 n 2 + 8 mnk + 4 b 2 + 4 a 2 k 2 − m 2 k 2 − n 2 + 2 mnk + b 2 + a 2 k 2 ( a 2 − m 2 ) k 2 + 2 mnk + b 2 − n 2 ( a 2 − m 2 ) k 2 + 2 mnk + a 2 − m 2 a 2 n 2 − n 2 ( a 2 − m 2 ) k 2 + 2 mnk + a 2 − m 2 m 2 n 2 b 2 a 2 n 2 k 2 + 2 mnk + a 2 b 2 m 2 ( b an k + a bm ) 2 k = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = 0 = − a 2 n b 2 m 代入点 P ( m , n ) P(m,n) P ( m , n ) l : y − n = − b 2 m a 2 n ( x − m ) l:y-n=-\frac{b^2m}{a^2n}(x-m) l : y − n = − a 2 n b 2 m ( x − m ) l : m a 2 x + n b 2 y = 1 l:\frac{m}{a^2}x+\frac{n}{b^2}y=1 l : a 2 m x + b 2 n y = 1
接下来证明抛物线的情况,设抛物线方程 C : y 2 = 2 p x C:y^2=2px C : y 2 = 2 p x n 2 = 2 p m n^2=2pm n 2 = 2 p m
仍然设切线 l : y − n = k ( x − m ) l:y-n=k(x-m) l : y − n = k ( x − m ) y = k x − m k + n y=kx-mk+n y = k x − mk + n
{ y = k x − m k + n y 2 = 2 p x \begin{cases}
y=kx-mk+n
\\y^2=2px
\end{cases} { y = k x − mk + n y 2 = 2 p x 得:
k 2 x 2 + m 2 k 2 + n 2 − 2 m k 2 x + 2 n k x − 2 m n k = 2 p x k 2 x 2 + ( 2 n k + 2 m k 2 − 2 p ) x + m 2 k 2 + n 2 − 2 m n k = 0 Δ = 0 ( 2 n k + 2 m k 2 − 2 p ) 2 − 4 k 2 ( m 2 k 2 + n 2 − 2 m n k ) = 0 4 n 2 k 2 + 4 m 2 k 4 + 4 p 2 + 8 m n k 3 − 8 p n k − 8 p m k 2 − 4 m 2 k 4 − 4 n 2 k 2 + 8 m n k 3 = 0 4 p 2 − 8 p n k − 8 p m k 2 = 0 p 2 − 2 p n k − n 2 k 2 = 0 ( n k − p ) 2 = 0 k = p n \begin{aligned}
k^2x^2+m^2k^2+n^2-2mk^2x+2nkx-2mnk&=2px
\\k^2x^2+(2nk+2mk^2-2p)x+m^2k^2+n^2-2mnk&=0
\\\Delta&=0
\\(2nk+2mk^2-2p)^2-4k^2(m^2k^2+n^2-2mnk)&=0
\\\cancel{4n^2k^2}+\cancel{4m^2k^4}+4p^2+\cancel{8mnk^3}-8pnk-8pmk^2-\cancel{4m^2k^4}-\cancel{4n^2k^2}+\cancel{8mnk^3}&=0
\\4p^2-8pnk-8pmk^2&=0
\\p^2-2pnk-n^2k^2&=0
\\(nk-p)^2&=0
\\k&=\frac{p}{n}
\end{aligned} k 2 x 2 + m 2 k 2 + n 2 − 2 m k 2 x + 2 nk x − 2 mnk k 2 x 2 + ( 2 nk + 2 m k 2 − 2 p ) x + m 2 k 2 + n 2 − 2 mnk Δ ( 2 nk + 2 m k 2 − 2 p ) 2 − 4 k 2 ( m 2 k 2 + n 2 − 2 mnk ) 4 n 2 k 2 + 4 m 2 k 4 + 4 p 2 + 8 mn k 3 − 8 p nk − 8 p m k 2 − 4 m 2 k 4 − 4 n 2 k 2 + 8 mn k 3 4 p 2 − 8 p nk − 8 p m k 2 p 2 − 2 p nk − n 2 k 2 ( nk − p ) 2 k = 2 p x = 0 = 0 = 0 = 0 = 0 = 0 = 0 = n p 代入点 P ( m , n ) P(m,n) P ( m , n ) l : y − n = p n ( x − m ) l:y-n=\frac{p}{n}(x-m) l : y − n = n p ( x − m ) l : n y = p x + p m l:ny=px+pm l : n y = p x + p m
证毕。
拓展变形 :
在本节证明中,我们反复运用圆锥曲线方程找到 a 2 a^2 a 2 b 2 b^2 b 2 m 2 m^2 m 2 n 2 n^2 n 2
微拓展——隐函数求导法求解切线方程
高中所学的求导方法均是对形如 y = … y=\dots y = … y 2 y^2 y 2
例如有椭圆方程 E : x 2 9 + y 2 4 = 1 E:\frac{x^2}{9}+\frac{y^2}{4}=1 E : 9 x 2 + 4 y 2 = 1
椭圆方程是一个隐函数,对其求导。简单来讲分如下几步:
按照标准求导法则,对每一项按照高中所学的求导法则计算。此时 E 1 : 2 x 9 + 2 y 4 = 0 E_1:\frac{2x}{9}+\frac{2y}{4}=0 E 1 : 9 2 x + 4 2 y = 0
(这是隐函数求导的关键一步)在所有 y y y y ′ y^\prime y ′ y ′ y^\prime y ′ E ′ : 2 x 9 + 2 y y ′ 4 = 0 E^\prime:\frac{2x}{9}+\frac{2yy^\prime}{4}=0 E ′ : 9 2 x + 4 2 y y ′ = 0
移项解出 y ′ y^\prime y ′ y ′ = − 4 x 9 y y^\prime=-\frac{4x}{9y} y ′ = − 9 y 4 x
得到了导数,令 y ′ = 0 y^\prime=0 y ′ = 0 x = 0 x=0 x = 0 y = ± 2 y=\pm2 y = ± 2 2 {2} 2
再如给定的抛物线方程 C : y 2 = 4 x C:y^2=4x C : y 2 = 4 x ( 1 , 2 ) (1,2) ( 1 , 2 ) 2 y y ′ = 4 2yy^\prime=4 2 y y ′ = 4 y ′ = 2 y y^\prime=\frac{2}{y} y ′ = y 2 k = 1 k=1 k = 1 y = x + 1 y=x+1 y = x + 1 y = x + 1 y=x+1 y = x + 1
如果并非标准(中心不一定在原点、不一定关于坐标轴对称)的椭圆方程怎么办?假设非标准的方程是 E : x 2 4 + 3 x y + y 2 8 − 8 = 0 E:\frac{x^2}{4}+3xy+\frac{y^2}{8}-8=0 E : 4 x 2 + 3 x y + 8 y 2 − 8 = 0 ( 0 , 8 ) (0,8) ( 0 , 8 )
E ′ : x 2 + 3 y + 3 x y ′ + y y ′ 4 = 0 y ′ = − x 2 + 3 y y 4 + 3 x \begin{aligned}
E^\prime:\frac{x}{2}+3y+3xy^\prime+\frac{yy^\prime}{4}&=0
y^\prime&=-\dfrac{\frac{x}{2}+3y}{\frac{y}{4}+3x}
\end{aligned} E ′ : 2 x + 3 y + 3 x y ′ + 4 y y ′ = 0 y ′ = − 4 y + 3 x 2 x + 3 y 代入点 ( 0 , 8 ) (0,8) ( 0 , 8 ) k = − 12 k=-12 k = − 12 l : y = − 12 x + 8 l:y=-12x+8 l : y = − 12 x + 8 x y xy x y ( x y ) ′ = 1 y + x y ′ (xy)^\prime=1y+xy^\prime ( x y ) ′ = 1 y + x y ′ x x x y y y y ′ y^\prime y ′
隐函数相关知识在后面的新定义曲线的极值计算有大用。
切点弦方程# 切点弦方程的计算方法与切线方程的计算方法一模一样,它们之间有什么奇妙的联系?
评析 :证明需要利用同构方程的思想。对初识者来讲可能稍难理解。
证明 :
设曲线外一点 P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 ) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 )
以椭圆为例,可得 A P : x 1 a 2 x + y 1 b 2 y = 1 , B P : x 2 a 2 x + y 2 b 2 y = 1 AP:\frac{x_1}{a^2}x+\frac{y_1}{b^2}y=1,BP:\frac{x_2}{a^2}x+\frac{y^2}{b^2}y=1 A P : a 2 x 1 x + b 2 y 1 y = 1 , BP : a 2 x 2 x + b 2 y 2 y = 1 P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 )
A P : x 0 x 1 a 2 + y 0 y 1 b 2 = 1 B P : x 0 x 2 a 2 + y 0 y 2 b 2 = 1 AP:\frac{x_0x_1}{a^2}+\frac{y_0y_1}{b^2}=1
\\BP:\frac{x_0x_2}{a^2}+\frac{y_0y_2}{b^2}=1 A P : a 2 x 0 x 1 + b 2 y 0 y 1 = 1 BP : a 2 x 0 x 2 + b 2 y 0 y 2 = 1 将 a , b , x 0 , y 0 a,b,x_0,y_0 a , b , x 0 , y 0 f ( X , Y ) = x 0 a 2 X + y 0 b 2 Y = 1 f(X,Y)=\frac{x_0}{a^2}X+\frac{y_0}{b^2}Y=1 f ( X , Y ) = a 2 x 0 X + b 2 y 0 Y = 1 A , B ∈ f ( X , Y ) A,B\in f(X,Y) A , B ∈ f ( X , Y ) f ( X , Y ) f(X,Y) f ( X , Y ) A B AB A B A B : x 0 a 2 x + y 0 b 2 = 1 AB:\frac{x_0}{a^2}x+\frac{y_0}{b^2}=1 A B : a 2 x 0 x + b 2 y 0 = 1
证毕。
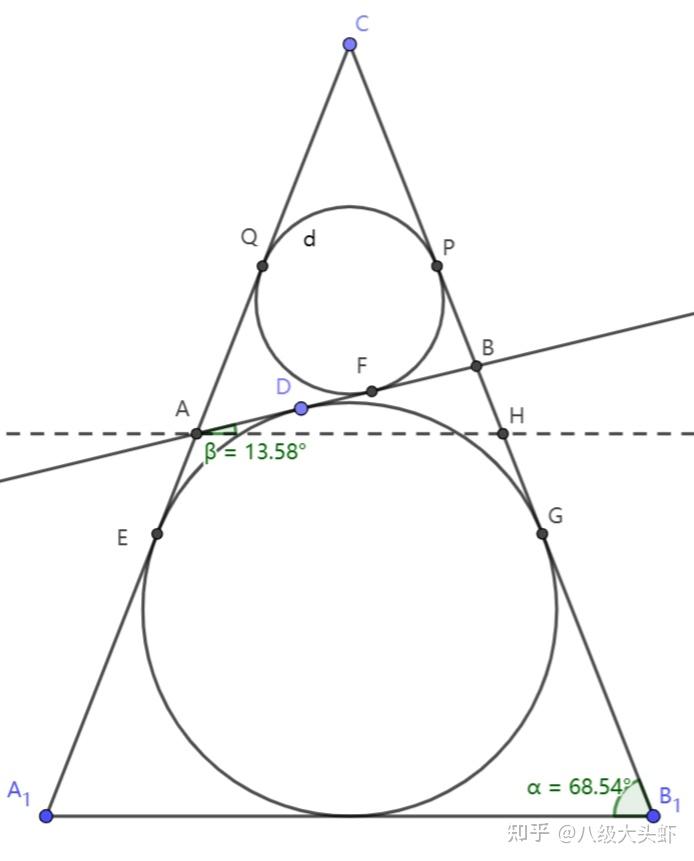
Dandelin \texttt{Dandelin} Dandelin # 用一个不垂直于圆锥的轴的平面截圆锥,当圆锥的轴与截面所成的角不同时,可以得到不同的截口曲线,它们分别是椭圆、抛物线和双曲线,我们通常把椭圆、抛物线、双曲线统称为圆锥曲线 (conic sections)
人教版 A 版高中数学《选择性必修 第一册》第三章引言
很多同学十分了解圆锥曲线的求法、形状以及特征量关系,但是对它的起源却知之甚少。顾名思义,圆锥曲线必定和“圆锥”有关。事实上——正如引言所说,用一个不垂直圆锥的轴的平面去截圆锥,若得到一个平面,那么该截面的形状必定是椭圆、双曲线、抛物线其一,见下图:
从上至下分别是圆、椭圆、抛物线和双曲线 图片来源于知乎
当然,也存在一些特殊情形。例如当截面过圆锥顶点时,可能截出一个点,此时我们称这个圆锥曲线是退化的。退化的圆锥曲线在高中阶段没有讨论的必要,因此后文所有的圆锥曲线如无特殊说明均指代非退化的圆锥曲线。
了解了圆锥曲线的来源,那么我们将以何种方式求解这个截面曲线(圆锥曲线)的解析式呢?如果表示出平面和圆锥,再硬算交集曲线,显然划不来。200 多年前,人们发现了 Dandelin \texttt{Dandelin} Dandelin
图源知乎
该模型的主要内容是(椭圆为例):两个球体与圆锥内表面相切,同时与形成圆锥曲线(此处为椭圆)的截面相切,它们与截面的交点为这个圆锥曲线(此处为椭圆)的两个焦点,因此 Dandelin \texttt{Dandelin} Dandelin
截口曲线# 设双球与截口曲线的切点分别为 F 1 , F 2 F_1,F_2 F 1 , F 2
评析 :可以利用切线长定理的三维形式来解决。
证明 :
本结论证明过程中的标记与下图相同:
图片截取自 Bilibili@寻秋灯下客
根据切线长定理的扩展,可得线段长满足 P F 1 = P K 1 , P F 2 = P K 2 PF_1=PK_1,PF_2=PK_2 P F 1 = P K 1 , P F 2 = P K 2 P F 1 + P F 2 = P K 1 + P K 2 = A D PF_1+PF_2=PK_1+PK_2=AD P F 1 + P F 2 = P K 1 + P K 2 = A D A D AD A D A D AD A D 2 a 2a 2 a F 1 , F 2 F_1,F_2 F 1 , F 2
证毕。
拓展变形 :关于切线长定理及其三维扩展形式。
我们初中就知道,过圆外一点引圆的两条切线,那么该点与两个切点分别连成的线段长度相等。那么为什么这个结论放在球体中也成立呢?先来看看推论内容:
在三维空间中,过球体外一点引球体的若干切线,那么这些切线长均相等。
只引出两条切线时,过这两个切点可以截出一个圆形,此时与二维形式相同。如果切线多于两条,我们可以将球外的点与球心相连,然后连接球心与切点,它与切线必垂直,因此所有切线长度均为 D 2 − R 2 \sqrt{D^2-R^2} D 2 − R 2 D D D R R R
图源知乎
如图,Dandelin \texttt{Dandelin} Dandelin E Q = P G = A B = 2 a , B H = 2 c EQ=PG=AB=2a,BH=2c EQ = PG = A B = 2 a , B H = 2 c
评析 :利用切线长定理可以证明该结论。
证明 :
根据切线长定理,左侧母线有 A Q = A F , A D = A E AQ=AF,AD=AE A Q = A F , A D = A E B P = B F , B D = B G BP=BF,BD=BG BP = BF , B D = BG A D + A F = B F + B D = E Q = P G AD+AF=BF+BD=EQ=PG A D + A F = BF + B D = EQ = PG
该模型的已知条件是:A , B A,B A , B A B = 2 a AB=2a A B = 2 a D F = 2 c DF=2c D F = 2 c A H / / A 1 B 1 AH// A_1B_1 A H // A 1 B 1 A E = G H AE=GH A E = G H
对等式两边同时减去公共线段长 D F DF D F 2 A D = 2 B F → A D = B F {2}AD=2BF\rightarrow AD=BF 2 A D = 2 BF → A D = BF E Q = A D + A F = B F + A F = A B = 2 a EQ=AD+AF=BF+AF=AB=2a EQ = A D + A F = BF + A F = A B = 2 a P G = A B = 2 a PG=AB=2a PG = A B = 2 a a , c a,c a , c B D = B G = a + c , B F = a − c BD=BG=a+c,BF=a-c B D = BG = a + c , BF = a − c B H = B G − G H = B G − A E = B G − A D = B D − A D = ( a + c ) − ( a − c ) = 2 c BH=BG-GH=BG-AE=BG-AD=BD-AD=(a+c)-(a-c)=2c B H = BG − G H = BG − A E = BG − A D = B D − A D = ( a + c ) − ( a − c ) = 2 c
证毕。
离心率# 如上图,截面截出的圆锥曲线离心率为 e = sin β sin α e=\frac{\sin\beta}{\sin\alpha} e = s i n α s i n β α , β \alpha,\beta α , β ∠ A H C , ∠ B A H \angle AHC,\angle BAH ∠ A H C , ∠ B A H e = cos γ cos θ e=\frac{\cos\gamma}{\cos\theta} e = c o s θ c o s γ γ , θ \gamma,\theta γ , θ A B , A C AB,AC A B , A C
评析 :在 △ A B H \triangle ABH △ A B H
证明 :
在 △ A B H \triangle ABH △ A B H e = B H A B = c a = sin β sin α e=\frac{BH}{AB}=\frac{c}{a}=\frac{\sin\beta}{\sin\alpha} e = A B B H = a c = s i n α s i n β cos γ cos θ \frac{\cos\gamma}{\cos\theta} c o s θ c o s γ
证毕。
仿射变换# 我们接下来要用一个颇具线性代数色彩(JustPureH 2 O 色彩)的章节来为圆锥曲线的相关面积问题铺路,它就是“仿射变换”。通过对原图形进行适当拉伸变换,将复杂的圆锥曲线转换成特殊的、简单的几何图形(一般是圆)来简化计算。借用仿射变换的知识,我们可以证明椭圆的面积公式,并一定程度上解释椭圆不存在精确的周长公式的根本原因。在探讨这两个问题前,我们先引入仿射变换的相关内容:
仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间的过程。
简单来说就是对一个图形进行平移、缩放(整体缩放/方向缩放)、旋转等变换。例如椭圆 E : x 2 4 + y 2 = 1 E:\frac{x^2}{4}+y^2=1 E : 4 x 2 + y 2 = 1 x x x 2 {2} 2 E ′ : x 2 + y 2 = 1 E^\prime:x^2+y^2=1 E ′ : x 2 + y 2 = 1
仿射变换前后,原图形/若干相关图形有几个不变的量/关系:
共线性:共线的若干点在变换后仍共线
平行性:两平行直线在变换后仍平行
等比性:某线段上的点将该线段分为长度 a : b a:b a : b a : b a:b a : b
第一条性质是明显的;对于第二条、第三条,我们可以借用物理的正交分解思想来解决:在原平行直线上各取两点,算出斜率 k = Δ y Δ x k=\frac{\Delta y}{\Delta x} k = Δ x Δ y k ′ = m Δ y n Δ n k^\prime=\frac{m\Delta y}{n\Delta n} k ′ = n Δ n m Δ y
从上面三条基本性质可以进一步推出——当仿射变换的内容是将图形在 x x x a a a y y y b b b a × b a\times b a × b x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 a 2 x 2 + b 2 y 2 = 1 S = π a b S=\pi ab S = πab x 2 + y 2 = 1 x^2+y^2=1 x 2 + y 2 = 1 x x x a a a y y y b b b
但是,某线段在经过仿射变换后,其长度并非简单满足“按比缩放”的关系。这点可以借用物理的正交分解思想来证明:假如一条线段,在 x , y x,y x , y a , b a,b a , b a = 2 , b = 3 a=2,b=3 a = 2 , b = 3
原线段长度为 11.25 \sqrt{11.25} 11.25 7.5 {7.5} 7.5 a , b a,b a , b L = Δ x 2 + Δ y 2 , L ′ = a 2 Δ x 2 + b 2 Δ y 2 L=\sqrt{\Delta x^2+\Delta y^2},L^\prime=\sqrt{a^2\Delta x^2+b^2\Delta y^2} L = Δ x 2 + Δ y 2 , L ′ = a 2 Δ x 2 + b 2 Δ y 2
利用仿射变换,我们可以轻松证得蒙日圆中部分面积相关问题的二级结论。
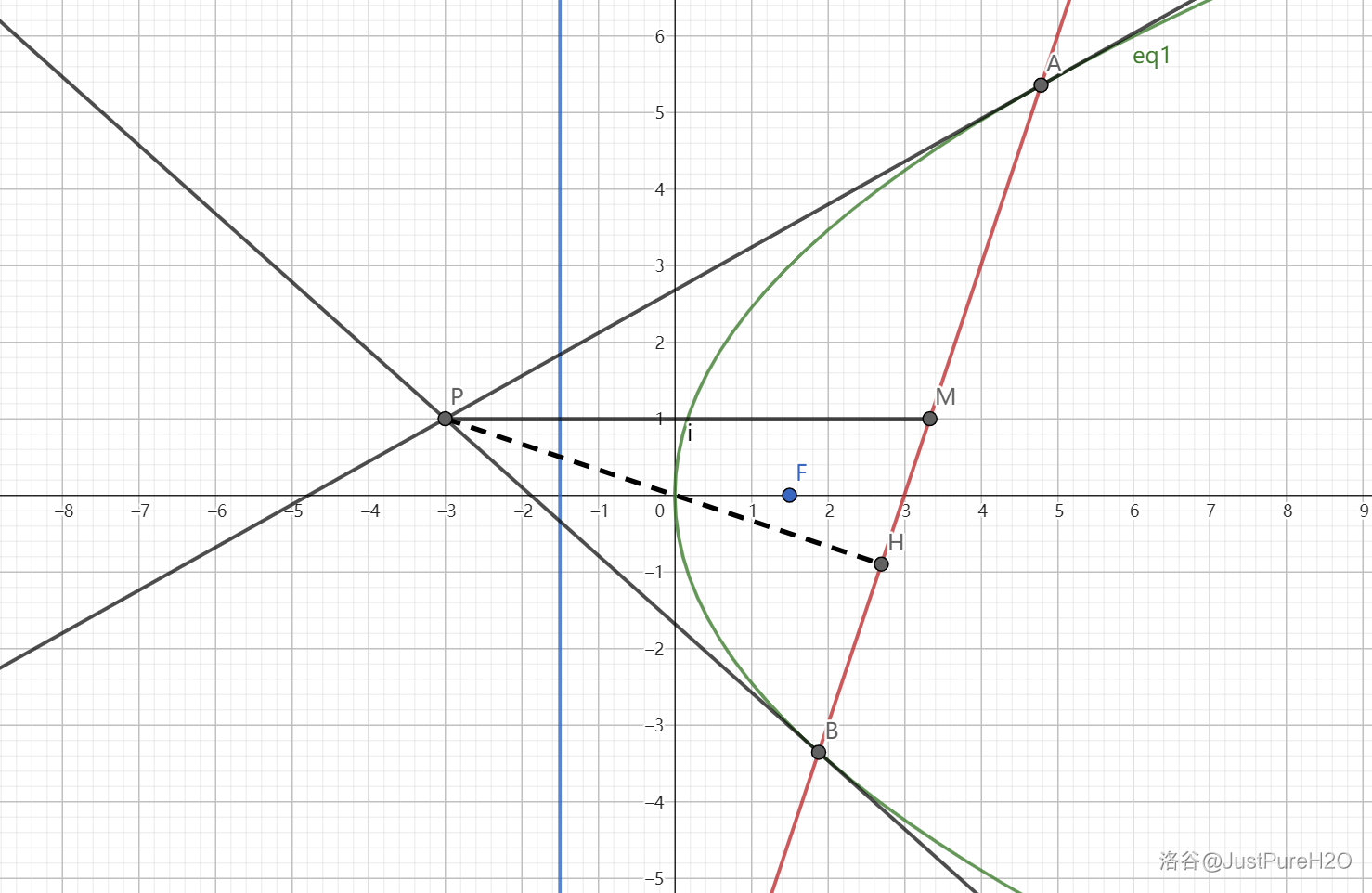
蒙日圆# 椭圆 E E E x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 a 2 x 2 + b 2 y 2 = 1 x 2 + y 2 = a 2 + b 2 x^2+y^2=a^2+b^2 x 2 + y 2 = a 2 + b 2
若无特殊说明,两切线交于 P P P A A A B B B C C C D D D
轨迹方程(解析法)# 椭圆 E E E x 2 + y 2 = a 2 + b 2 x^2+y^2=a^2+b^2 x 2 + y 2 = a 2 + b 2
评析 :没有感情,只有设点。
证明 :
切线斜率不存在时,P ( ± a , ± b ) P(\pm a,\pm b) P ( ± a , ± b ) x 2 + y 2 = a 2 + b 2 x^2+y^2=a^2+b^2 x 2 + y 2 = a 2 + b 2
切线斜率存在时,设 P M : y = k x + m PM:y=kx+m PM : y = k x + m P N : y = − 1 k x + n PN:y=-\frac{1}{k}x+n PN : y = − k 1 x + n
联立 P M PM PM
( b 2 + a 2 k 2 ) x 2 + 2 a 2 m k x + a 2 m 2 − a 2 b 2 = 0 Δ = 0 4 a 4 m 2 k 2 − 4 a 2 ( b 2 + a 2 k 2 ) ( m 2 − b 2 ) = 0 a 2 k 2 + b 2 − m 2 = 0 m 2 = a 2 k 2 + b 2 \begin{aligned}
(b^2+a^2k^2)x^2+2a^2mkx+a^2m^2-a^2b^2&=0
\\\Delta&=0
\\4a^4m^2k^2-4a^2(b^2+a^2k^2)(m^2-b^2)&=0
\\a^2k^2+b^2-m^2&=0
\\m^2&=a^2k^2+b^2
\end{aligned} ( b 2 + a 2 k 2 ) x 2 + 2 a 2 mk x + a 2 m 2 − a 2 b 2 Δ 4 a 4 m 2 k 2 − 4 a 2 ( b 2 + a 2 k 2 ) ( m 2 − b 2 ) a 2 k 2 + b 2 − m 2 m 2 = 0 = 0 = 0 = 0 = a 2 k 2 + b 2 同理可得 a 2 k 2 + b 2 − n 2 = 0 → a 2 + b 2 k 2 = n 2 k 2 \frac{a^2}{k^2}+b^2-n^2=0\rightarrow a^2+b^2k^2=n^2k^2 k 2 a 2 + b 2 − n 2 = 0 → a 2 + b 2 k 2 = n 2 k 2
联立两直线方程得到 P ( k ( n − m ) k 2 + 1 , n k 2 + m k 2 + 1 ) P\left(\frac{k(n-m)}{k^2+1},\frac{nk^2+m}{k^2+1}\right) P ( k 2 + 1 k ( n − m ) , k 2 + 1 n k 2 + m ) ∣ O P ∣ 2 = n 2 k 2 + m 2 k 2 + 1 = a 2 + b 2 k 2 + a 2 k 2 + b 2 k 2 + 1 = a 2 + b 2 |OP|^2=\frac{n^2k^2+m^2}{k^2+1}=\frac{a^2+b^2k^2+a^2k^2+b^2}{k^2+1}=a^2+b^2 ∣ OP ∣ 2 = k 2 + 1 n 2 k 2 + m 2 = k 2 + 1 a 2 + b 2 k 2 + a 2 k 2 + b 2 = a 2 + b 2 P P P x 2 + y 2 = a 2 + b 2 x^2+y^2=a^2+b^2 x 2 + y 2 = a 2 + b 2
证毕。
轨迹方程(几何法)# 该方法由一位与我同班的数竞大佬提供。证明相关辅助线如下图:
证明 :
点 A A A E E E A , B A,B A , B F 1 , F 2 F_1,F_2 F 1 , F 2 A B , A C AB,AC A B , A C F 1 ′ , F 2 ′ F_1^\prime,F_2^\prime F 1 ′ , F 2 ′
由椭圆光学性质可得,F 1 , C , F 2 ′ F_1,C,F_2^\prime F 1 , C , F 2 ′ F 2 , B , F 1 ′ F_2,B,F_1^\prime F 2 , B , F 1 ′ A F 1 = A F 1 ′ , A F 2 = A F 2 ′ , B F 1 = B F 1 ′ , A F 2 = A F 2 ′ AF_1=AF_1^\prime,AF_2=AF_2^\prime,BF_1=BF_1^\prime,AF_2=AF_2^\prime A F 1 = A F 1 ′ , A F 2 = A F 2 ′ , B F 1 = B F 1 ′ , A F 2 = A F 2 ′ F 1 ′ F 2 = F 2 ′ F 1 = 2 a = F_1^\prime F_2=F_2^\prime F_1=2a= F 1 ′ F 2 = F 2 ′ F 1 = 2 a =
三边相等,据此判定 △ A F 2 F 1 ′ ≅ △ A F 2 ′ F 1 \triangle AF_2F_1^\prime\cong\triangle AF_2^\prime F_1 △ A F 2 F 1 ′ ≅ △ A F 2 ′ F 1 ∠ F 1 A F 2 ′ = ∠ F 1 ′ A F 2 \angle F_1AF_2^\prime=\angle F_1^\prime AF_2 ∠ F 1 A F 2 ′ = ∠ F 1 ′ A F 2
同时减去公共角 ∠ F 1 A F 2 \angle F_1AF_2 ∠ F 1 A F 2 ∠ F 1 ′ A F 1 = ∠ F 2 ′ A F 2 \angle F_1^\prime AF_1=\angle F_2^\prime AF_2 ∠ F 1 ′ A F 1 = ∠ F 2 ′ A F 2 ∠ F 1 ′ A D = ∠ D A F 1 = ∠ F 2 A E = ∠ E A F 2 ′ \angle F_1^\prime AD=\angle DAF_1=\angle F_2AE=\angle EAF_2^\prime ∠ F 1 ′ A D = ∠ D A F 1 = ∠ F 2 A E = ∠ E A F 2 ′
已知 ∠ B A C = 90 ° \angle BAC=90\degree ∠ B A C = 90° ∠ F 1 A F 2 ′ = ∠ F 1 A E + ∠ E A F 2 ′ = ∠ F 1 A E + ∠ D A F 1 = ∠ B A C = 90 ° = ∠ F 1 ′ A F 2 \angle F_1AF_2^\prime=\angle F_1AE+\angle EAF_2^\prime=\angle F_1AE+\angle DAF_1=\angle BAC=90\degree=\angle F_1^\prime AF_2 ∠ F 1 A F 2 ′ = ∠ F 1 A E + ∠ E A F 2 ′ = ∠ F 1 A E + ∠ D A F 1 = ∠ B A C = 90° = ∠ F 1 ′ A F 2
在有公共边的两三角形 △ A O F 1 , △ A O F 2 \triangle AOF_1,\triangle AOF_2 △ A O F 1 , △ A O F 2 ∠ A O F 1 + ∠ A O F 2 = 180 ° \angle AOF_1+\angle AOF_2=180\degree ∠ A O F 1 + ∠ A O F 2 = 180°
cos ∠ A O F 1 + cos ∠ A O F 2 = 0 ∣ O A ∣ 2 + ∣ O F 1 ∣ 2 − ∣ A F 1 ∣ 2 2 ∣ O A ∣ ∣ O F 1 ∣ + ∣ O A ∣ 2 + ∣ O F 2 ∣ 2 − ∣ A F 2 2 ∣ 2 ∣ O A ∣ ∣ O F 2 ∣ = 0 2 ∣ O A ∣ 2 + ∣ O F 1 ∣ 2 + ∣ O F 2 ∣ 2 − ∣ A F 1 ∣ 2 − ∣ A F 2 ∣ 2 = 0 ∣ O A ∣ 2 = ∣ A F 1 ∣ 2 + ∣ A F 2 ∣ 2 2 − c 2 = ∣ F 1 F 2 ′ ∣ 2 2 − c 2 = ( ∣ C F 1 ∣ + ∣ C F 2 ∣ ) 2 2 − c 2 = 2 a 2 − c 2 = a 2 + b 2 \begin{aligned}
\cos\angle AOF_1+\cos\angle AOF_2&=0
\\\frac{|OA|^2+|OF_1|^2-|AF_1|^2}{2|OA||OF_1|}+\frac{|OA|^2+|OF_2|^2-|AF_2^2|}{2|OA||OF_2|}&=0
\\2|OA|^2+|OF_1|^2+|OF_2|^2-|AF_1|^2-|AF_2|^2&=0
\end{aligned}
\\\begin{aligned}
\\|OA|^2&=\frac{|AF_1|^2+|AF_2|^2}{2}-c^2
\\&=\frac{|F_1F_2^\prime|^2}{2}-c^2
\\&=\frac{(|CF_1|+|CF_2|)^2}{2}-c^2
\\&=2a^2-c^2
\\&=a^2+b^2
\end{aligned} cos ∠ A O F 1 + cos ∠ A O F 2 2∣ O A ∣∣ O F 1 ∣ ∣ O A ∣ 2 + ∣ O F 1 ∣ 2 − ∣ A F 1 ∣ 2 + 2∣ O A ∣∣ O F 2 ∣ ∣ O A ∣ 2 + ∣ O F 2 ∣ 2 − ∣ A F 2 2 ∣ 2∣ O A ∣ 2 + ∣ O F 1 ∣ 2 + ∣ O F 2 ∣ 2 − ∣ A F 1 ∣ 2 − ∣ A F 2 ∣ 2 = 0 = 0 = 0 ∣ O A ∣ 2 = 2 ∣ A F 1 ∣ 2 + ∣ A F 2 ∣ 2 − c 2 = 2 ∣ F 1 F 2 ′ ∣ 2 − c 2 = 2 ( ∣ C F 1 ∣ + ∣ C F 2 ∣ ) 2 − c 2 = 2 a 2 − c 2 = a 2 + b 2 证毕。
几何性质 其一# 蒙日圆上一点 P P P C , D C,D C , D C D CD C D
评析 :无
证明 :
根据圆内直径所对的圆周角恒为直角的关系,可得 C D CD C D C , O , D C,O,D C , O , D C D CD C D
证毕。
广义垂径定理# P P P P P P E E E P A , P B PA,PB P A , PB A , B A,B A , B O P OP OP k O P ⋅ k A B = − b 2 a 2 k_{OP}\cdot k_{AB}=-\frac{b^2}{a^2} k OP ⋅ k A B = − a 2 b 2
评析 :利用圆锥曲线的切点弦方程即可快速解决。
证明 :
令 P ( x 0 , y 0 ) P(x_0,y_0) P ( x 0 , y 0 ) k O P = y 0 x 0 k_{OP}=\frac{y_0}{x_0} k OP = x 0 y 0 A B : x 0 a 2 x + y 0 b 2 y = 1 AB:\frac{x_0}{a^2}x+\frac{y_0}{b^2}y=1 A B : a 2 x 0 x + b 2 y 0 y = 1 k A B = − b 2 x 0 a 2 y 0 k_{AB}=-\frac{b^2x_0}{a^2y_0} k A B = − a 2 y 0 b 2 x 0 − b 2 a 2 -\frac{b^2}{a^2} − a 2 b 2
证毕。
拓展变形 :椭圆交点所在坐标轴变化后仍然会变成 − a 2 b 2 -\frac{a^2}{b^2} − b 2 a 2 A B AB A B O P OP OP M M M A B AB A B
几何性质 其二# 蒙日圆上一点 P P P P A PA P A P B PB PB A , B A,B A , B C , D C,D C , D O P OP OP A B AB A B M M M A B / / C D AB//CD A B // C D
评析 :利用几何关系进行证明。前置是上面的广义垂径定理和几何性质一。
证明 :
根据蒙日圆,得到顶角 ∠ A P B = 90 ° \angle APB=90\degree ∠ A PB = 90° M M M A B AB A B P M = P A = P B PM=PA=PB PM = P A = PB ∠ A P O = ∠ O A P \angle APO=\angle OAP ∠ A PO = ∠ O A P P C D PCD PC D ∠ D C P = ∠ O A P \angle DCP=\angle OAP ∠ D CP = ∠ O A P ∠ D C P = ∠ A P O \angle DCP=\angle APO ∠ D CP = ∠ A PO
证毕。
拓展变形 :根据这条性质,广义垂径定理可以推广成 k O P ⋅ k C D = − b 2 a 2 k_{OP}\cdot k_{CD}=-\frac{b^2}{a^2} k OP ⋅ k C D = − a 2 b 2
几何性质 其三# 从蒙日圆上一点 P P P E E E P A , P B PA,PB P A , PB A , B A,B A , B k O A k A P = k O B k B P = − b 2 a 2 , k O A k O B = − b 4 a 4 k_{OA}k_{AP}=k_{OB}k_{BP}=-\frac{b^2}{a^2},k_{OA}k_{OB}=-\frac{b^4}{a^4} k O A k A P = k OB k BP = − a 2 b 2 , k O A k OB = − a 4 b 4
评析 :运用切线公式和已知的垂直条件快速解题。
证明 :
令 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) P A : x 1 a 2 x + y 1 b 2 y = 1 PA:\frac{x_1}{a^2}x+\frac{y_1}{b^2}y=1 P A : a 2 x 1 x + b 2 y 1 y = 1 − b 2 x 1 a 2 y 1 -\frac{b^2x_1}{a^2y_1} − a 2 y 1 b 2 x 1 − b 2 x 1 a 2 y 1 ⋅ y 1 x 1 = − b 2 a 2 -\frac{b^2x_1}{a^2y_1}\cdot\frac{y_1}{x_1}=-\frac{b^2}{a^2} − a 2 y 1 b 2 x 1 ⋅ x 1 y 1 = − a 2 b 2 k O B k P B = − b 2 a 2 k_{OB}k_{PB}=-\frac{b^2}{a^2} k OB k PB = − a 2 b 2
综合以上两式 k O A k P A = k O B k P B = − b 2 a 2 k_{OA}k_{PA}=k_{OB}k_{PB}=-\frac{b^2}{a^2} k O A k P A = k OB k PB = − a 2 b 2 k O A k O B k P A k P B = b 4 a 4 k_{OA}k_{OB}k_{PA}k_{PB}=\frac{b^4}{a^4} k O A k OB k P A k PB = a 4 b 4 k P A k P B = − 1 k_{PA}k_{PB}=-1 k P A k PB = − 1 k O A k O B = − b 4 a 4 k_{OA}k_{OB}=-\frac{b^4}{a^4} k O A k OB = − a 4 b 4
证毕。
阿基米德三角形# 抛物线的某条弦 A B AB A B A , B A,B A , B P P P P A B PAB P A B
△ A B P \triangle ABP △ A BP △ C D Q \triangle CDQ △ C D Q
若无特殊说明,本章中的抛物线 E E E y 2 = 2 p x ( p > 0 ) y^2=2px(p>0) y 2 = 2 p x ( p > 0 )
几何性质 其一# 阿基米德三角形在抛物线上的弦的中点为 M M M P P P P M / / x PM//x PM // x
评析 :巧妙运用切线方程解决问题。
证明 :
令弦的端点 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) x 1 = y 1 2 2 p , x 2 = y 2 2 2 p x_1=\frac{y_1^2}{2p},x_2=\frac{y_2^2}{2p} x 1 = 2 p y 1 2 , x 2 = 2 p y 2 2 P A : y 1 y = p x + p x 1 PA:y_1y=px+px_1 P A : y 1 y = p x + p x 1 P B : y 2 y = p x + p x 2 PB:y_2y=px+px_2 PB : y 2 y = p x + p x 2 P ( y 1 y 2 2 p , y 1 + y 2 2 ) P(\frac{y_1y_2}{2p},\frac{y_1+y_2}{2}) P ( 2 p y 1 y 2 , 2 y 1 + y 2 ) M ( y 1 2 + y 2 2 4 p , y 1 + y 2 2 ) M(\frac{y_1^2+y_2^2}{4p},\frac{y_1+y_2}{2}) M ( 4 p y 1 2 + y 2 2 , 2 y 1 + y 2 ) P M / / x PM//x PM // x
证毕。
几何性质 其二# 当阿基米德三角形在抛物线上的弦过定点 G ( x 0 , y 0 ) G(x_0,y_0) G ( x 0 , y 0 ) y 0 y = p ( x + x 0 ) y_0y=p(x+x_0) y 0 y = p ( x + x 0 )
评析 :利用切点弦公式,或者是几何性质一可以证明。此处选用几何性质一进行证明。
证明 :
令底边 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) P ( y 1 y 2 2 , y 1 + y 2 2 ) P(\frac{y_1y_2}{2},\frac{y_1+y_2}{2}) P ( 2 y 1 y 2 , 2 y 1 + y 2 ) G G G A B AB A B k A B = k A G k_{AB}=k_{AG} k A B = k A G
y 2 − y 1 x 2 − x 1 = y 1 − y 0 x 1 − x 0 y 2 − y 1 y 2 2 2 p − y 1 2 2 p = 2 p y 1 + y 2 = y 1 − y 0 y 1 2 2 p − x 0 y 1 2 − 2 p x 0 = y 1 2 + y 1 y 2 − y 0 ( y 1 + y 2 ) 2 p x 0 = y 0 ( y 1 + y 2 ) − y 1 y 2 2 p x 0 = 2 y 0 y p − 2 x p y 0 y p = p ( x 0 + x p ) \begin{aligned}
\dfrac{y_2-y_1}{x_2-x_1}&=\dfrac{y_1-y_0}{x_1-x_0}
\\\dfrac{y_2-y_1}{\frac{y_2^2}{2p}-\frac{y_1^2}{2p}}=\dfrac{2p}{y_1+y_2}&=\dfrac{y_1-y_0}{\frac{y_1^2}{2p}-x_0}
\\y_1^2-2px_0&=y_1^2+y_1y_2-y_0(y_1+y_2)
\\2px_0&=y_0(y_1+y_2)-y_1y_2
\\2px_0&=2y_0y_p-2x_p
\\y_0y_p&=p(x_0+x_p)
\end{aligned} x 2 − x 1 y 2 − y 1 2 p y 2 2 − 2 p y 1 2 y 2 − y 1 = y 1 + y 2 2 p y 1 2 − 2 p x 0 2 p x 0 2 p x 0 y 0 y p = x 1 − x 0 y 1 − y 0 = 2 p y 1 2 − x 0 y 1 − y 0 = y 1 2 + y 1 y 2 − y 0 ( y 1 + y 2 ) = y 0 ( y 1 + y 2 ) − y 1 y 2 = 2 y 0 y p − 2 x p = p ( x 0 + x p ) 因此 P P P y 0 y = p ( x + x 0 ) y_0y=p(x+x_0) y 0 y = p ( x + x 0 )
证毕。
拓展变形 :此结论的推论有——当底边过焦点时,顶点的轨迹为抛物线准线;底边过 x x x ( a , 0 ) (a,0) ( a , 0 ) x = − a x=-a x = − a
几何性质 其三# 当阿基米德三角形的底边过焦点时,阿基米德三角形的顶角为 90 ° {90}\degree 90 ° P A ⊥ P B PA\perp PB P A ⊥ PB
评析 :可以借助几何性质一来快速解决。
证明 :
令 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) P ( y 1 y 2 2 p , y 1 + y 2 2 ) P(\frac{y_1y_2}{2p},\frac{y_1+y_2}{2}) P ( 2 p y 1 y 2 , 2 y 1 + y 2 )
k 1 k 2 = y 1 − y 1 + y 2 2 x 1 − y 1 y 2 2 p × y 2 − y 1 + y 2 2 x 2 − y 1 y 2 2 p = y 1 − y 2 2 y 1 2 − y 1 y 2 2 p × y 2 − y 1 2 y 2 2 − y 1 y 2 2 p = p ( y 1 − y 2 ) y 1 ( y 1 − y 2 ) × p ( y 2 − y 1 ) y 2 ( y 2 − y 1 ) = p 2 y 1 y 2 \begin{aligned}
k_1k_2&=\dfrac{y_1-\frac{y_1+y_2}{2}}{x_1-\frac{y_1y_2}{2p}}\times\dfrac{y_2-\frac{y_1+y_2}{2}}{x_2-\frac{y_1y_2}{2p}}
\\&=\dfrac{\frac{y_1-y_2}{2}}{\frac{y_1^2-y_1y_2}{2p}}\times\dfrac{\frac{y_2-y_1}{2}}{\frac{y_2^2-y_1y_2}{2p}}
\\&=\dfrac{p(y_1-y_2)}{y_1(y_1-y_2)}\times\dfrac{p(y_2-y_1)}{y_2(y_2-y_1)}
\\&=\dfrac{p^2}{y_1y_2}
\end{aligned} k 1 k 2 = x 1 − 2 p y 1 y 2 y 1 − 2 y 1 + y 2 × x 2 − 2 p y 1 y 2 y 2 − 2 y 1 + y 2 = 2 p y 1 2 − y 1 y 2 2 y 1 − y 2 × 2 p y 2 2 − y 1 y 2 2 y 2 − y 1 = y 1 ( y 1 − y 2 ) p ( y 1 − y 2 ) × y 2 ( y 2 − y 1 ) p ( y 2 − y 1 ) = y 1 y 2 p 2 最后联系到抛物线焦点弦定理中 y 1 y 2 = − p 2 y_1y_2=-p^2 y 1 y 2 = − p 2 − 1 -1 − 1
证毕。
几何性质 其四# 在阿基米德三角形中,恒有 ∠ P F A = ∠ P F B \angle PFA=\angle PFB ∠ PF A = ∠ PFB
评析 :几何法搭配解析几何解题较为快速。
证明 :
过 A , B A,B A , B A A 1 , B B 1 AA_1,BB_1 A A 1 , B B 1 A 1 , B 1 A_1,B_1 A 1 , B 1 A 1 P , B 1 P , A 1 F A_1P,B_1P,A_1F A 1 P , B 1 P , A 1 F A 1 F ∩ A P = O A_1F\cap AP=O A 1 F ∩ A P = O
令 A ( x 1 , y 1 ) , B ( x 2 , y 2 ) A(x_1,y_1),B(x_2,y_2) A ( x 1 , y 1 ) , B ( x 2 , y 2 ) P A : y = p y 1 x + p x 1 y 1 PA:y=\frac{p}{y_1}x+\frac{px_1}{y_1} P A : y = y 1 p x + y 1 p x 1 k P A = p y 1 k_{PA}=\frac{p}{y_1} k P A = y 1 p A 1 ( − p 2 , y 1 ) A_1(-\frac{p}{2},y_1) A 1 ( − 2 p , y 1 ) A 1 F A_1F A 1 F − y 1 p -\frac{y_1}{p} − p y 1 − 1 -1 − 1 A P ⊥ A 1 F AP\perp A_1F A P ⊥ A 1 F
在抛物线中,有 ∣ A A 1 ∣ = ∣ A F ∣ |AA_1|=|AF| ∣ A A 1 ∣ = ∣ A F ∣ △ A 1 A O ≅ △ F A O \triangle A_1AO\cong\triangle FAO △ A 1 A O ≅ △ F A O ∠ A 1 A O = ∠ F A O \angle A_1AO=\angle FAO ∠ A 1 A O = ∠ F A O △ A 1 A P ≅ △ F A P \triangle A_1AP\cong\triangle FAP △ A 1 A P ≅ △ F A P
仿照上述全等推导可证得 △ B F P ≅ △ B B 1 P \triangle BFP\cong\triangle BB_1P △ BFP ≅ △ B B 1 P ∠ P F B = ∠ B B 1 P , ∠ P F A = ∠ P A 1 A \angle PFB=\angle BB_1P,\angle PFA=\angle PA_1A ∠ PFB = ∠ B B 1 P , ∠ PF A = ∠ P A 1 A
根据几何性质一可得,y P = y 1 + y 2 2 y_P=\frac{y_1+y_2}{2} y P = 2 y 1 + y 2 A 1 P = B 1 P A_1P=B_1P A 1 P = B 1 P ∠ P A 1 B 1 = ∠ P B 1 A 1 \angle PA_1B_1=\angle PB_1A_1 ∠ P A 1 B 1 = ∠ P B 1 A 1 ∠ P A 1 A = ∠ P B 1 B = 90 ° + ∠ P A 1 B 1 \angle PA_1A=\angle PB_1B=90\degree+\angle PA_1B_1 ∠ P A 1 A = ∠ P B 1 B = 90° + ∠ P A 1 B 1 ∠ P F B = ∠ P F A \angle PFB=\angle PFA ∠ PFB = ∠ PF A
证毕。
几何性质 其五# 在阿基米德三角形中,有 ∣ A F ∣ ⋅ ∣ B F ∣ = ∣ P F ∣ 2 |AF|\cdot|BF|=|PF|^2 ∣ A F ∣ ⋅ ∣ BF ∣ = ∣ PF ∣ 2
评析 :根据性质一得出的点的坐标代入计算即可验证。
证明 :
根据性质一可得 P ( y 1 y 2 2 p , y 1 + y 2 2 ) P(\frac{y_1y_2}{2p},\frac{y_1+y_2}{2}) P ( 2 p y 1 y 2 , 2 y 1 + y 2 ) ∣ P F ∣ 2 = ( y 1 y 2 2 p − p 2 ) 2 + ( y 1 + y 2 2 ) 2 = p 2 4 + y 1 2 y 2 2 4 p 2 + y 1 2 + y 2 2 4 |PF|^2=(\frac{y_1y_2}{2p}-\frac{p}{2})^2+(\frac{y_1+y_2}{2})^2=\frac{p^2}{4}+\frac{y_1^2y_2^2}{4p^2}+\frac{y_1^2+y_2^2}{4} ∣ PF ∣ 2 = ( 2 p y 1 y 2 − 2 p ) 2 + ( 2 y 1 + y 2 ) 2 = 4 p 2 + 4 p 2 y 1 2 y 2 2 + 4 y 1 2 + y 2 2
同时,在抛物线中满足 ∣ A F ∣ = x A + p 2 = y 1 2 2 p + p 2 |AF|=x_A+\frac{p}{2}=\frac{y_1^2}{2p}+\frac{p}{2} ∣ A F ∣ = x A + 2 p = 2 p y 1 2 + 2 p ∣ B F ∣ = x B + p 2 = y 2 2 2 p + p 2 |BF|=x_B+\frac{p}{2}=\frac{y_2^2}{2p}+\frac{p}{2} ∣ BF ∣ = x B + 2 p = 2 p y 2 2 + 2 p
∣ A F ∣ ⋅ ∣ B F ∣ = ( y 1 2 2 p + p 2 ) × ( y 2 2 2 p + p 2 ) = y 1 2 y 2 2 4 p 2 + p 2 4 + y 1 2 + y 2 2 4 = ∣ Q F ∣ 2 \begin{aligned}
|AF|\cdot|BF|&=\left(\frac{y_1^2}{2p}+\frac{p}{2}\right)\times\left(\frac{y_2^2}{2p}+\frac{p}{2}\right)
\\&=\frac{y_1^2y_2^2}{4p^2}+\frac{p^2}{4}+\frac{y_1^2+y_2^2}{4}
\\&=|QF|^2
\end{aligned} ∣ A F ∣ ⋅ ∣ BF ∣ = ( 2 p y 1 2 + 2 p ) × ( 2 p y 2 2 + 2 p ) = 4 p 2 y 1 2 y 2 2 + 4 p 2 + 4 y 1 2 + y 2 2 = ∣ QF ∣ 2 证毕。
几何性质 其六# 底边 A B AB A B a a a a 3 8 p \frac{a^3}{8p} 8 p a 3
评析 :利用三角形面积等于底乘高除以二,再对高的长度进行放缩即可。
证明 :
如图:P H PH P H △ A P B \triangle APB △ A PB A B AB A B M M M A B AB A B A B : x = k y + b AB:x=ky+b A B : x = k y + b
易知 ∣ P H ∣ ≤ ∣ P M ∣ |PH|\leq|PM| ∣ P H ∣ ≤ ∣ PM ∣ A B ⊥ x AB\perp x A B ⊥ x ∣ A B ∣ = a = ( k 2 + 1 ) ( y 1 − y 2 ) 2 ≥ ( y 1 − y 2 ) 2 |AB|=a=\sqrt{(k^2+1)(y_1-y_2)^2}\geq\sqrt{(y_1-y_2)^2} ∣ A B ∣ = a = ( k 2 + 1 ) ( y 1 − y 2 ) 2 ≥ ( y 1 − y 2 ) 2
根据性质一,P ( y 1 y 2 2 p , y 1 + y 2 2 ) P(\frac{y_1y_2}{2p},\frac{y_1+y_2}{2}) P ( 2 p y 1 y 2 , 2 y 1 + y 2 ) M ( x 1 + x 2 2 , y 1 + y 2 2 ) M(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}) M ( 2 x 1 + x 2 , 2 y 1 + y 2 ) ∣ P M ∣ = x 1 + x 2 2 − y 1 y 2 2 p = y 1 2 + y 2 2 4 p − y 1 y 2 2 p = ( y 1 − y 2 ) 2 4 p |PM|=\frac{x_1+x_2}{2}-\frac{y_1y_2}{2p}=\frac{y_1^2+y_2^2}{4p}-\frac{y_1y_2}{2p}=\frac{(y_1-y_2)^2}{4p} ∣ PM ∣ = 2 x 1 + x 2 − 2 p y 1 y 2 = 4 p y 1 2 + y 2 2 − 2 p y 1 y 2 = 4 p ( y 1 − y 2 ) 2
此时 S △ A P B ≤ 1 2 a ( y 1 − y 2 ) 2 4 p ≤ a 3 8 p S_{\triangle APB}\leq\frac{1}{2}a\frac{(y_1-y_2)^2}{4p}\leq\frac{a^3}{8p} S △ A PB ≤ 2 1 a 4 p ( y 1 − y 2 ) 2 ≤ 8 p a 3 A B ⊥ x AB\perp x A B ⊥ x
证毕。
带旋圆锥曲线 / 非标准型圆锥曲线# 旋转变换# 点 P ( x , y ) P(x,y) P ( x , y ) θ \theta θ P 1 ( x cos θ + y sin θ , − x sin θ + y cos θ ) P_1(x\cos\theta+y\sin\theta,-x\sin\theta+y\cos\theta) P 1 ( x cos θ + y sin θ , − x sin θ + y cos θ ) θ \theta θ P 2 ( x cos θ − y sin θ , x sin θ + y cos θ ) P_2(x\cos\theta-y\sin\theta,x\sin\theta+y\cos\theta) P 2 ( x cos θ − y sin θ , x sin θ + y cos θ )
评析 :如果你了解线性变换的相关知识,你就会知道这其实是乘旋转矩阵得到的结果。但如果你不知道,我们可以不用线性代数知识,现场推导一番。
证明 :
令 P ( x , y ) P(x,y) P ( x , y ) O P OP OP x x x φ \varphi φ x = ∣ O P ∣ cos φ , y = ∣ O P ∣ sin φ x=|OP|\cos\varphi,y=|OP|\sin\varphi x = ∣ OP ∣ cos φ , y = ∣ OP ∣ sin φ sin φ = y ∣ O P ∣ , cos φ = x ∣ O P ∣ \sin\varphi=\frac{y}{|OP|},\cos\varphi=\frac{x}{|OP|} sin φ = ∣ OP ∣ y , cos φ = ∣ OP ∣ x x A = ∣ O P ∣ cos ( φ − α ) , y A = ∣ O P ∣ sin ( φ − α ) x_A=|OP|\cos(\varphi-\alpha),y_A=|OP|\sin(\varphi-\alpha) x A = ∣ OP ∣ cos ( φ − α ) , y A = ∣ OP ∣ sin ( φ − α ) x A x_A x A
x A = ∣ O P ∣ cos ( φ − α ) = ∣ O P ∣ ( cos φ cos α + sin φ sin α ) = ∣ O P ∣ cos φ cos α + ∣ O P ∣ sin φ sin α = ∣ O P ∣ x ∣ O P ∣ cos α + ∣ O P ∣ y ∣ O P ∣ sin α = x cos α + y sin α \begin{aligned}
x_A&=|OP|\cos(\varphi-\alpha)
\\&=|OP|(\cos\varphi\cos\alpha+\sin\varphi\sin\alpha)
\\&=|OP|\cos\varphi\cos\alpha+|OP|\sin\varphi\sin\alpha
\\&=|OP|\frac{x}{|OP|}\cos\alpha+|OP|\frac{y}{|OP|}\sin\alpha
\\&=x\cos\alpha+y\sin\alpha
\end{aligned} x A = ∣ OP ∣ cos ( φ − α ) = ∣ OP ∣ ( cos φ cos α + sin φ sin α ) = ∣ OP ∣ cos φ cos α + ∣ OP ∣ sin φ sin α = ∣ OP ∣ ∣ OP ∣ x cos α + ∣ OP ∣ ∣ OP ∣ y sin α = x cos α + y sin α 同理可得 y A = − x sin α + y cos α y_A=-x\sin\alpha+y\cos\alpha y A = − x sin α + y cos α B B B
证毕。
拓展变形 :
如何将这一点运用到圆锥曲线上来呢?我们根据这个原理,联想到圆锥曲线的旋转本质上是将曲线上每一个点都做旋转变换,每个点的横纵坐标变换都满足如上规则。因此如果将圆锥曲线写成一个函数形式 f ( x , y ) f(x,y) f ( x , y ) f ( x cos θ + y sin θ , − x sin θ + y cos θ ) f(x\cos\theta+y\sin\theta,-x\sin\theta+y\cos\theta) f ( x cos θ + y sin θ , − x sin θ + y cos θ )
当然,旋转后的圆锥曲线与原圆锥曲线的形状是相同的。这意味着圆锥曲线的离心率等由其本身形状所决定的量不会发生改变,但是垂径定理、圆周定理将不再适用。
解平移# 当某个非标准型圆锥曲线的解析式不含 x y xy x y x , y x,y x , y
联系三角函数图像的相关知识,f ( x ) = sin 2 x f(x)=\sin2x f ( x ) = sin 2 x f ( x + π 6 ) = sin ( 2 x + π 3 ) f\left(x+\frac{\pi}{6}\right)=\sin\left(2x+\frac{\pi}{3}\right) f ( x + 6 π ) = sin ( 2 x + 3 π ) f ( x ) f(x) f ( x ) π 6 \frac{\pi}{6} 6 π f ( x , y ) : x 2 a 2 + y 2 b 2 = 1 f(x,y):\frac{x^2}{a^2}+\frac{y^2}{b^2}=1 f ( x , y ) : a 2 x 2 + b 2 y 2 = 1 f ( x + 1 , y − 2 ) : ( x + 1 ) 2 a 2 + ( y − 2 ) 2 b 2 = 1 f(x+1,y-2):\frac{(x+1)^2}{a^2}+\frac{(y-2)^2}{b^2}=1 f ( x + 1 , y − 2 ) : a 2 ( x + 1 ) 2 + b 2 ( y − 2 ) 2 = 1 1 {1} 1 2 {2} 2
据此,假设现在有一个方程 9 x 2 + y 2 + 6 x + 2 y − 3 = 0 9x^2+y^2+6x+2y-3=0 9 x 2 + y 2 + 6 x + 2 y − 3 = 0
9 x 2 + y 2 + 6 x + 2 y − 3 = 0 ( 3 x + 1 ) 2 + ( y + 1 ) 2 = 5 ( 3 x + 1 ) 2 5 + ( y + 1 ) 2 5 = 1 ( x + 1 3 ) 2 45 + ( y + 1 ) 2 5 = 1 \begin{aligned}
9x^2+y^2+6x+2y-3&=0
\\(3x+1)^2+(y+1)^2&=5
\\\frac{(3x+1)^2}{5}+\frac{(y+1)^2}{5}&=1
\\\frac{\left(x+\frac{1}{3}\right)^2}{45}+\frac{(y+1)^2}{5}&=1
\end{aligned} 9 x 2 + y 2 + 6 x + 2 y − 3 ( 3 x + 1 ) 2 + ( y + 1 ) 2 5 ( 3 x + 1 ) 2 + 5 ( y + 1 ) 2 45 ( x + 3 1 ) 2 + 5 ( y + 1 ) 2 = 0 = 5 = 1 = 1 易知该圆锥曲线为 E : 9 x 2 5 + y 2 5 = 1 E:\frac{9x^2}{5}+\frac{y^2}{5}=1 E : 5 9 x 2 + 5 y 2 = 1 1 3 \frac{1}{3} 3 1 1 {1} 1
除开专门的圆锥曲线大题,圆锥曲线,尤其是非标准型的圆锥曲线,往往会在你意想不到的地方出现。例如 2024 年天津卷填空压轴:
若函数 f ( x ) = 2 x 2 − a x − ∣ a x − 2 ∣ + 1 f(x)=2\sqrt{x^2-ax}-|ax-2|+1 f ( x ) = 2 x 2 − a x − ∣ a x − 2∣ + 1 a a a
很多人此时会想移项平方以消去根号和绝对值,而忽略了一个东西,那就是根号项,它可以处理成一个函数图像:
y = x 2 − a x y 2 = x 2 − a x x 2 − y 2 + a x = 0 ( x + a 2 ) 2 − y 2 = a 2 4 4 ( x + a 2 ) 2 a 2 − 4 y 2 a 2 = 1 \begin{aligned}
\begin{aligned}
y&=\sqrt{x^2-ax}
\\y^2&=x^2-ax
\end{aligned}
\\\begin{aligned}
\\x^2-y^2+ax&=0
\\\left(x+\frac{a}{2}\right)^2-y^2&=\frac{a^2}{4}
\\\dfrac{4\left(x+\frac{a}{2}\right)^2}{a^2}-\dfrac{4y^2}{a^2}&=1
\end{aligned}
\end{aligned} y y 2 = x 2 − a x = x 2 − a x x 2 − y 2 + a x ( x + 2 a ) 2 − y 2 a 2 4 ( x + 2 a ) 2 − a 2 4 y 2 = 0 = 4 a 2 = 1 它是一个平移的双曲线,并且考虑到平方根的性质,它是该双曲线在 y ≥ 0 y\geq0 y ≥ 0
解旋转# 当某个非标准型圆锥曲线的解析式中含有 x y xy x y x , y x,y x , y
法一 图像性质# 以方才结束的(以撰写此节的日期 2025 年 12 月 27 日为准)2025 年成都一诊多选压轴为例:
2025 年成都市高中毕业班第一次诊断性考试 T11
首先你需要相信出题人,要告诉自己这个(高考)是面向全国中学生 的招生性考试,所以这个旋转变换多半是特殊的。我们仍然把第一个式子 x 2 + y 2 − x y − 4 = 0 x^2+y^2-xy-4=0 x 2 + y 2 − x y − 4 = 0 f ( x , y ) f(x,y) f ( x , y ) x , y x,y x , y f ( y , x ) f(y,x) f ( y , x ) f ( x , y ) f(x,y) f ( x , y ) y = x y=x y = x A B C ABC A BC
假如你想知道它是由哪个曲线旋转得到,可以选择用旋转变换来把它变回标准型圆锥曲线,即用(θ = 45 ° \theta=45\degree θ = 45° 2 2 x − 2 2 y \frac{\sqrt2}{2}x-\frac{\sqrt2}{2}y 2 2 x − 2 2 y x x x 2 2 x + 2 2 y \frac{\sqrt2}{2}x+\frac{\sqrt2}{2}y 2 2 x + 2 2 y y y y x 2 8 + 3 y 2 8 = 1 \frac{x^2}{8}+\frac{3y^2}{8}=1 8 x 2 + 8 3 y 2 = 1
法二 特征值# 如果函数不满足 f ( x , y ) = f ( y , x ) f(x,y)=f(y,x) f ( x , y ) = f ( y , x )
值得注意的是,这种非 45 ° {45\degree} 45°
河北省保定市四校联考 2025-2026 学年高三上期 9 月月考数学试卷 T14
答案的做法是解出两个渐近线,首先代入 x = + ∞ x=+\infty x = + ∞ x x x 0 {0} 0 l 1 : 3 4 x l_1:\frac{3}{4}x l 1 : 4 3 x y = + ∞ y=+\infty y = + ∞ x → 0 x\rightarrow0 x → 0 l 2 : x = 0 l_2:x=0 l 2 : x = 0 y y y
根据旋转,两渐近线夹角 θ \theta θ tan θ 2 = b a \tan\frac{\theta}{2}=\frac{b}{a} tan 2 θ = a b b a = 2 \frac{b}{a}=2 a b = 2 e = 1 + b 2 a 2 = 5 e=\sqrt{1+\frac{b^2}{a^2}}=\sqrt5 e = 1 + a 2 b 2 = 5
接下来讲解特征值做法:
对于一般型二次曲线方程 A x 2 + B x y + C y 2 + D x + E y + F = 0 Ax^2+Bxy+Cy^2+Dx+Ey+F=0 A x 2 + B x y + C y 2 + D x + E y + F = 0 A x 2 + B x y + C y 2 = 0 Ax^2+Bxy+Cy^2=0 A x 2 + B x y + C y 2 = 0
x M x T = [ x y ] [ A B 2 B 2 C ] [ x y ] xMx^T=\begin{bmatrix}
x&y
\end{bmatrix}
\begin{bmatrix}
A&\frac{B}{2}
\\\frac{B}{2}&C
\end{bmatrix}
\begin{bmatrix}
x\\y
\end{bmatrix} x M x T = [ x y ] [ A 2 B 2 B C ] [ x y ] 矩阵乘法相关运算法则见此 。
接下来求解 M M M 2 × 2 {2\times2} 2 × 2 tr ( M ) = m 11 + m 22 , det ( M ) = m 11 m 22 − m 12 m 21 \operatorname{tr}(M)=m_{11}+m_{22},\det(M)=m_{11}m_{22}-m_{12}m_{21} tr ( M ) = m 11 + m 22 , det ( M ) = m 11 m 22 − m 12 m 21 λ 1 , λ 2 \lambda_1,\lambda_2 λ 1 , λ 2
{ λ 1 + λ 2 = tr ( M ) = A + C λ 1 λ 2 = det ( M ) = B 2 4 − A C \begin{cases}
\lambda_1+\lambda_2=\operatorname{tr}(M)=A+C
\\\lambda_1\lambda_2=\det(M)=\frac{B^2}{4}-AC
\end{cases} { λ 1 + λ 2 = tr ( M ) = A + C λ 1 λ 2 = det ( M ) = 4 B 2 − A C 解得:
λ = A + C ± ( A − C ) 2 + B 2 2 \lambda=\frac{A+C\pm\sqrt{(A-C)^2+B^2}}{2} λ = 2 A + C ± ( A − C ) 2 + B 2 接下来任取一个特征值,例如 λ 1 \lambda_1 λ 1 M M M
M ′ = [ A − λ 1 B 2 B 2 C − λ 1 ] M^\prime=\begin{bmatrix}
A-\lambda_1&\frac{B}{2}
\\\frac{B}{2}&C-\lambda_1
\end{bmatrix} M ′ = [ A − λ 1 2 B 2 B C − λ 1 ] 此时,M ′ M^\prime M ′ a ⃗ \vec a a x ⃗ ′ , y ⃗ ′ \vec x^\prime,\vec y^\prime x ′ , y ′ x ⃗ = ( 1 , 0 ) \vec x=(1,0) x = ( 1 , 0 ) v e c y = ( 0 , 1 ) vec y=(0,1) v ecy = ( 0 , 1 )
以该题为例,构造矩阵得 M = [ 3 4 − 1 2 − 1 2 0 ] M=\begin{bmatrix}\frac{3}{4}&-\frac{1}{2}\\-\frac{1}{2}&0\end{bmatrix} M = [ 4 3 − 2 1 − 2 1 0 ] λ 1 = 1 , λ 2 = − 1 4 \lambda_1=1,\lambda_2=-\frac{1}{4} λ 1 = 1 , λ 2 = − 4 1 λ 1 = 1 \lambda_1=1 λ 1 = 1 M ′ = [ − 1 4 − 1 2 − 1 2 − 1 ] M^\prime=\begin{bmatrix}-\frac{1}{4}&-\frac{1}{2}\\-\frac{1}{2}&-1\end{bmatrix} M ′ = [ − 4 1 − 2 1 − 2 1 − 1 ]
提取,转为单位向量 a ⃗ = ( 2 5 5 , 5 5 ) \vec a=\left(\frac{2\sqrt5}{5},\frac{\sqrt5}{5}\right) a = ( 5 2 5 , 5 5 ) x x x cos θ = 2 5 5 \cos\theta=\frac{2\sqrt5}{5} cos θ = 5 2 5 E : x 2 − y 2 2 = 1 E:x^2-\frac{y^2}{2}=1 E : x 2 − 2 y 2 = 1 e = 5 e=\sqrt5 e = 5