抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

基础数据结构 线段树

oi算法

发布于：2024年8月8日

字数：18.1k 字

时长：88 分钟

旧专栏由于年久失修，目前已被标记为过时。本文是对旧博客的重写及内容补充。

线段树的思想就是把一段区间拆分成两个子区间，运用递归的方式，线段树能在不大规模改动原数组的情况下实现区间信息的维护。有了这一点，区间信息维护的时间复杂度就从朴素暴力算法的 优化到了 。

前言

本文所使用的宏定义及含义如下：

宏名 定义 作用
le(x) (x * 2) 获取左子树的下标
ri(x) (x * 2 + 1) 获取右子树的下标
leftSubtree(idx) tree[le(idx)] 获取左子树对象
rightSubtree(idx) tree[ri(idx)] 获取右子树对象

线段树的建树

根据前文所说，线段树将一段长区间分为两段，并设为它自身的子树，不断递归直到区间长度为 。如下图：

可见线段树是一棵满二叉树，它有 个节点（ 为树的高度/层数，上图中 ）；此外还可以发现，对于下标为 的节点，如果它存在子树，那么它的左子树的下标就是 、右子树为 。我们平常使用线段树，则需要开四倍的空间（pushdown 位置的不同、删去某些特判可能会让这一上限最多变为八倍空间，后文将阐述其原因）。

在建树时，我们需要处理出当前区间的中点，并分别递归左右子树继续建树、顺带维护区间左右端点的信息（区间大小、初始化懒标记等）。根据前文，递归终点是区间长度降落为 ，此时将原序列中的信息搬过去即可。

1
2
3
4
5
6
7
8
9
10
11
void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r; // 维护区间左右端点
    if (l == r) {
        tree[idx].max = a[l]; // 维护区间最大值
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid); // 递归左子树
    build(ri(idx), mid + 1, r); // 递归右子树
    pushup(idx); // 更新父节点
}

线段树的节点更新

基本分两种，已知子节点更新父节点和已知父节点更新子节点。

第一种操作一般被称作 pushup 上传操作。在子节点更新完毕回溯时进行，起到更新父节点的作用；第二种操作被称作 pushdown 下传操作。在带有懒标记的线段树中向子节点递归查找信息时进行，能够将先前积累起来的操作下放到子节点。

一般在编写上传操作时，要考虑到所维护信息的结合性质。例如维护区间和，父节点记录的值显然应该是左右子树记录的值之和；再比如维护区间最大值，显然应该是左右区间分别记录的最大值中更大的那一个。

1
2
3
4
5
void pushup(int idx) {
    tree[idx].max = max(leftSubtree(idx).max, rightSubtree(idx).max); // 区间最大值
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;     // 区间和
    // ...
}

在写标记下传时，需要特别考虑标记之间的优先级关系。例如当前有两个操作——区间推平（赋成统一的值）和区间加。当该区间需要下传一个推平标记时，可以直接把区间加标记给清空，因为推平后就不会存在区间加；反过来就不成立，因为区间可以在推平后继续进行加法。因此我们需要先判断推平标记的情况，后面再来处理区间加标记。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void pushdown(int idx) {
    if (tree[idx].que != -LLONG_MAX) { // 区间推平优先处理
        leftSubtree(idx).max = tree[idx].que;
        leftSubtree(idx).que = tree[idx].que; // 继承推平标记
        leftSubtree(idx).add = 0; // 清空加法标记
        rightSubtree(idx).max = tree[idx].que;
        rightSubtree(idx).que = tree[idx].que;
        rightSubtree(idx).add = 0; // 清空加法标记
        tree[idx].que = -LLONG_MAX; // 清空推平标记
    }
    if (tree[idx].add) { // 区间加法后处理
        leftSubtree(idx).max += tree[idx].add;
        leftSubtree(idx).add += tree[idx].add;
        rightSubtree(idx).max += tree[idx].add;
        rightSubtree(idx).add += tree[idx].add;

        tree[idx].add = 0;
    }
}

线段树的查询操作

线段树既可以查询单点信息，也可以查询整个区间的信息，前者可以看作是区间长度为 的区间查询，是区间查询的一类特殊情况。

简单查询

在这个例子中，我们假设查询区间 的某些信息，首先我们就需要找到这个区间：递归查找、缩小范围，发现当递归到下标 时，区间 就被包含了，于是直接返回；当查询至下标 ，区间 被包含进去，此时我们就可以不用花费大力气继续向下递归了，因为线段树的父节点就存储了子节点的信息。以查询区间最大值为例：

1
2
3
4
5
6
7
8
9
int queryMax(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].max; // 完全包含，直接返回
    pushdown(idx);   // 子节点可能存在积累的操作
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    int res = -INF;
    if (l <= mid) res = max(res, queryMax(le(idx), l, r)); // 递归左侧
    if (r > mid) res = max(res, queryMax(ri(idx), l, r));   // 递归右侧
    return res;
}

由于查询的值是独立的，不依赖于其他变量。如果碰到较为复杂的、多重依赖的变量，那么这种方法可能就会变得不那么适用了。接下来介绍第二种高级的查询操作，也可以说是码量较大但是更为万能的查询方法。

复杂查询

以查询区间最大子段和为例。我们维护了区间最大前缀、最大后缀以及最大子段和，最大子段和应是左子树最大前缀、右子树最大后缀以及左子树最大后缀加右子树最大前缀三者的最大值。如果依然沿用上面的简单查询，那么实现将会极其复杂，此时我们不再让函数返回线段树节点的某一权值，而是改成返回线段树节点本身。这样一来我们就可以通过左右子节点的值来推断返回值，从而达到查询的目的。查询逻辑和简单查询有不同：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
SegmentTree query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx];
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l > mid) return query(ri(idx), l, r);
    if (r <= mid) return query(le(idx), l, r);
    SegmentTree res{};
    SegmentTree L = query(le(idx), l, r);
    SegmentTree R = query(ri(idx), l, r);
    res.max = max(max(L.max, R.max), L.rmax + R.lmax);
    res.lmax = max(L.lmax, L.sum + R.lmax);
    res.rmax = max(R.rmax, R.sum + L.rmax);
    res.sum = L.sum + R.sum;
    return res;
}

首先，我们依然判断当前区间是否已被完全包含，若是则直接返回当前节点。接下来是不同之处：如果查询区间完全在中点右侧，那么返回右侧查询的结果，反之亦然，查询左侧。

如果区间不完全在中点一侧，那么左右分别查询，获得左右子节点的信息。接下来就可以按照正常的维护方法维护返回值节点的相关信息了。

线段树的修改操作

同样分为单点修改和区间修改，前者同样是后者的特殊情况。基本思路相同，先找到被完全包含的区间。但是此时可以有一个优化——不用每一次都递归到区间的叶子节点再进行修改，可以直接将修改信息记录在一个大区间内，当查询需要用到子节点的值时再一次性下放积累的操作。线段树中记录这些操作的标记便被称作懒标记。

对于某个区间，需要先把当前区间的相关信息修改之后再返回，否则相当于没有修改（只是打个标记，当前节点并未更新）。以区间加为例：

1
2
3
4
5
6
7
8
9
10
11
12
void modify(int idx, int l, int r, int x) {
    pushdown(idx); // 可能还有积累的操作
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].max += x; // 更新当前区间的最大值
        tree[idx].add += x; // 打标记
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x, type);
    if (r > mid) modify(ri(idx), l, r, x, type);
    pushup(idx); // 由于更新了当前节点，需要向上更新其他节点
}

一些细节

一句话，让评测结果从 RE 到 AC

有时你会发现——明明题目中说了 ，我也开了四倍空间，为什么还是会 RE？事实上，这可能是因为错误的 pushdown 位置和特判的缺乏。

比如下面这段区间修改的代码（来源 P2574 XOR的艺术）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void modify(int idx, int l, int r, int x) {
    pushdown(idx);
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].sum = x * tree[idx].size;
        tree[idx].que = x;
        tree[idx].lmax[x] = tree[idx].rmax[x] = tree[idx].max[x] = tree[idx].size;
        tree[idx].lmax[x ^ 1] = tree[idx].rmax[x ^ 1] = tree[idx].max[x ^ 1] = 0;
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

其中 ，代码中也是如此，但是最后有两个点 RE。这是因为 pushdown 放在了错误的位置上，在递归到单点前，会执行一次 pushdown 操作，此时就会在叶子节点的左右子树上检测懒标记（事实上没必要），在极端情况下，会访问到最后一个叶子节点的右子树（最坏 ），是肯定会 RE 的。把下传操作放在 l == r 的判断之后即可。

标记置零问题

有时，在下传操作中，在处理完当前标记之后是不能直接把标记置零的，例如（来源 P1253 扶苏的问题）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void pushdown(int idx) {
    if (tree[idx].que != -LLONG_MAX) {
        leftSubtree(idx).max = tree[idx].que;
        leftSubtree(idx).que = tree[idx].que;
        leftSubtree(idx).add = 0;
        rightSubtree(idx).max = tree[idx].que;
        rightSubtree(idx).que = tree[idx].que;
        rightSubtree(idx).add = 0;

        tree[idx].que = -LLONG_MAX;
        tree[idx].add = 0;
    }
    if (tree[idx].add) {
        leftSubtree(idx).max += tree[idx].add;
        leftSubtree(idx).add += tree[idx].add;
        rightSubtree(idx).max += tree[idx].add;
        rightSubtree(idx).add += tree[idx].add;

        tree[idx].add = 0;
    }
}

乍一看没什么问题，但是推平标记里 tree[idx].add = 0 却是造成 WA 的元凶。清空加运算标记，其实也就意味着把整段区间的区间加标记清空。然而在递归时是有可能向该区间的某个子区间递归的，于是当前区间就会有一头一尾的部分位置不需要被处理，但是你却把它们的区间加标记清空了，显然错误。正确做法是删去这一行。

简单应用

这些是线段树的基础维护问题，用来夯实线段树基础，为拓展线段树的高级思维做铺垫。

单调性判断

例题：P6812 「MCOI-02」Ancestor 先辈

难度：普及+/提高

维护变量：区间左右端点值、区间单调性标记

题目中的区间加因为比较板子故在此省去，我们只探讨区间单调性的维护方法。

对于叶子节点，必定满足单调性，我们只需考虑向上合并时的策略。注意到如果左右子树都满足单调性，那么能够决定整体区间单调性的就只有左子树的右端点和右子树的左端点的相对大小关系。故我们只需多维护当前区间的左右端点并在上传时维护单调性标记即可，维护方法见上面的分析。因为单调性标记的维护涉及到多个变量，查询时需要用到前面讲过的复杂查询。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <bits/stdc++.h>
#define N 1500010
using namespace std;

typedef long long ll;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(idx) (tree[le(idx)])
#define rightSubtree(idx) (tree[ri(idx)])
    int l, r, size;
    ll lazy;
    ll ends[2];
    bool flag; 
} tree[N << 2];
ll a[N];

void pushup(int idx) {
    tree[idx].flag = (leftSubtree(idx).flag & rightSubtree(idx).flag & (leftSubtree(idx).ends[1] <= rightSubtree(idx).ends[0])); // 单调递增序列需满足左子树的右端点小于等于右子树的左端点
    tree[idx].ends[0] = leftSubtree(idx).ends[0]; // 大区间的左端点就是左子树的左端点
    tree[idx].ends[1] = rightSubtree(idx).ends[1]; // 大区间的右端点就是右子树的右端点
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) {
        tree[idx].flag = true;
        tree[idx].ends[0] = tree[idx].ends[1] = a[l];
        return;
    }
    int mid = l + r >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void pushdown(int idx) {
    if (tree[idx].lazy) {
        leftSubtree(idx).lazy += tree[idx].lazy;
        leftSubtree(idx).ends[0] += tree[idx].lazy;
        leftSubtree(idx).ends[1] += tree[idx].lazy;
        rightSubtree(idx).lazy += tree[idx].lazy;
        rightSubtree(idx).ends[0] += tree[idx].lazy;
        rightSubtree(idx).ends[1] += tree[idx].lazy;

        tree[idx].lazy = 0;
    }
}

void modify(int idx, int l, int r, ll x) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].lazy += x;
        tree[idx].ends[0] += x;
        tree[idx].ends[1] += x;
        return;
    }
    pushdown(idx);
    int mid = tree[idx].l + tree[idx].r >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

// 复杂查询处理标记
SegmentTree query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx];
    pushdown(idx);
    int mid = tree[idx].l + tree[idx].r >> 1;
    if (l > mid) return query(ri(idx), l, r);
    if (r <= mid) return query(le(idx), l, r);
    SegmentTree L = query(le(idx), l, r);
    SegmentTree R = query(ri(idx), l, r);
    return {L.l, R.r, L.size + R.size, 0, {L.ends[0], R.ends[1]}, static_cast<bool>(L.flag & R.flag & (L.ends[1] <= R.ends[0]))};
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    while (k--) {
        int opt, l, r;
        cin >> opt >> l >> r;
        if (opt == 1) {
            ll x;
            cin >> x;
            modify(1, l, r, x);
        } else cout << (query(1, l, r).flag ? "Yes" : "No") << '\n';
    }

    return 0;
}

单点修改+区间乘积正负性

例题：UVA12532 Interval Product

难度：普及+/提高

维护变量：正负性标记

我们都知道，异号相乘得负、同号相乘得正。对于叶子节点，正负性是可以确定的。那么考虑上传操作，发现我们只需得知左右子树的正负性就可以得到当前区间的正负性。因此用一个正负性标记，取值 ，那么上传时就可以用左右子树的标记乘积来更新当前区间的正负性标记。单点修改非常模板此处不再赘述。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <bits/stdc++.h>
#define N 100010
using namespace std;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    int flag;
} tree[N << 2];
int a[N];

void pushup(int idx) {
    tree[idx].flag = leftSubtree(idx).flag * rightSubtree(idx).flag; // 更新标记为左右子树的标记之积
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) {
        if (a[l] == 0) tree[idx].flag = 0;
        if (a[l] > 0) tree[idx].flag = 1;
        if (a[l] < 0) tree[idx].flag = -1;
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int uid, int x) {
    if (tree[idx].size == 1 && tree[idx].l == uid) {
        if (x == 0) tree[idx].flag = 0;
        if (x > 0) tree[idx].flag = 1;
        if (x < 0) tree[idx].flag = -1;
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (uid <= mid) modify(le(idx), uid, x);
    if (uid > mid) modify(ri(idx), uid, x);
    pushup(idx);
}

int query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].flag;
    int flag = 1;
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) flag *= query(le(idx), l, r);
    if (r > mid) flag *= query(ri(idx), l, r);
    return flag;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, k;
    while (cin >> n >> k) {
        for (int i = 1; i <= n; i++) cin >> a[i];
        build(1, 1, n);
        while (k--) {
            char op;
            int l, r;
            cin >> op >> l >> r;
            if (op == 'C') modify(1, l, r);
            else {
                int res = query(1, l, r);
                cout << (res == 0 ? '0' : res < 0 ? '-' : '+');
            }
        }
        cout << endl;
    }

    return 0;
}

维护差分

线段树维护原序列的差分数组也是比较挑战思维的题型。通过维护原序列的差分序列，我们有时可以把一段区间的操作转化成对应区间端点或其邻点的单点操作。

种类数

例题：P2184 贪婪大陆

难度：普及+/提高

维护变量：区间和

像这种每次往某个区间加入一种不同种类的值，然后询问区间覆盖了几种不同的值，可以借助差分的思想。

将每个插入操作的区间看作有左右两个端点（起点、终点）的线段，因为每次插入的是不同种类的数，因此无需过多操作。对于每个 的询问，答案即为 内的起点数减去 内的终点数。也就是说 内有若干颜色段覆盖了一些区域，而 内又有一些颜色段没有覆盖到 及之后的区域，二者相减就是答案。

因此插入时暴力地增加两个端点的计数，输出时统计相减即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>

#define N 100010
using namespace std;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(idx) (tree[le(idx)])
#define rightSubtree(idx) (tree[ri(idx)])
    int l, r, size;
    int sum[2];
} tree[N << 2];

void pushup(int idx) {
    tree[idx].sum[0] = leftSubtree(idx).sum[0] + rightSubtree(idx).sum[0];
    tree[idx].sum[1] = leftSubtree(idx).sum[1] + rightSubtree(idx).sum[1];
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modifySt(int idx, int uid) {
    if (tree[idx].size == 1 && tree[idx].l == uid) {
        tree[idx].sum[0]++;
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (uid <= mid) modifySt(le(idx), uid);
    if (uid > mid) modifySt(ri(idx), uid);
    pushup(idx);
}

void modifyEd(int idx, int uid) {
    if (tree[idx].size == 1 && tree[idx].l == uid) {
        tree[idx].sum[1]++;
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (uid <= mid) modifyEd(le(idx), uid);
    if (uid > mid) modifyEd(ri(idx), uid);
    pushup(idx);
}

int querySt(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum[0];
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    int ret = 0;
    if (l <= mid) ret += querySt(le(idx), l, r);
    if (r > mid) ret += querySt(ri(idx), l, r);
    return ret;
}

int queryEd(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum[1];
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    int ret = 0;
    if (l <= mid) ret += queryEd(le(idx), l, r);
    if (r > mid) ret += queryEd(ri(idx), l, r);
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;
    build(1, 1, n);
    while (m--) {
        int q, l, r;
        cin >> q >> l >> r;
        if (q == 1) modifySt(1, l), modifyEd(1, r);
        else cout << querySt(1, 1, r) - queryEd(1, 1, l - 1) << endl;
    }
    return 0;
}

区间加等差数列、单点询问

例题：P1438 无聊的数列

难度：普及+/提高

维护变量：差分数组、区间和、区间和标记

注意到等差数列差分数组中的元素除左端点外都是其公差，因此我们维护原序列的差分数组。对原数组对位加等差数列就相当于让差分数组的左端点加上首项、中间点加上公差、右端点右侧第一个点减去末项。那么进行两次单点修改和一次区间修改即可。注意到差分的前缀和是对应的点权，所以统计前缀和即可回答单点询问。注意判断等差数列的长度！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include <bits/stdc++.h>

#define N 100100
using namespace std;

typedef long long ll;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    ll lazy, sum;
} tree[N << 2];
int a[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
}

void pushdown(int idx) {
    if (tree[idx].lazy) {
        leftSubtree(idx).sum += tree[idx].lazy * leftSubtree(idx).size;
        leftSubtree(idx).lazy += tree[idx].lazy;
        rightSubtree(idx).sum += tree[idx].lazy * rightSubtree(idx).size;
        rightSubtree(idx).lazy += tree[idx].lazy;

        tree[idx].lazy = 0;
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) {
        tree[idx].sum = a[l] - a[l - 1];
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, int x) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].lazy += x;
        tree[idx].sum += x * tree[idx].size;
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

void modify(int idx, int uid, int x) {
    if (tree[idx].size == 1 && tree[idx].l == uid) {
        tree[idx].sum += x;
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (uid <= mid) modify(le(idx), uid, x);
    if (uid > mid) modify(ri(idx), uid, x);
    pushup(idx);
}

ll query(int idx, int uid) {
    if (tree[idx].r <= uid) return tree[idx].sum;
    pushdown(idx);
    ll ret = 0;
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    ret += query(le(idx), uid);
    if (uid > mid) ret += query(ri(idx), uid);
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    while (m--) {
        int opt, l, r, k, d;
        cin >> opt >> l;
        if (opt == 1) {
            cin >> r >> k >> d;
            modify(1, l, k);
            if (l < r) modify(1, l + 1, r, d); // 数列长度为 1，仅单点修改
            if (r < n) modify(1, r + 1, (l - r) * d - k); // 右端点在最右侧，无需更改右端点右侧的差分
        } else cout << query(1, l) << endl;
    }

    return 0;
}

区间加+区间最大公约数

例题：P10463 Interval GCD

难度：提高+/省选-

维护变量：差分数组

属于是回归老祖宗的智慧了

OI 所学的最大公约数计算一般是欧几里得提出的辗转相除法，然而《九章算术》中提出的辗转相减法（更相减损术）却总是被人忽略。根据辗转相减法，，这个式子可以一直递归下去直到出现 的形式，答案就是 。这启发我们维护原序列的差分数组来操作，我们可以发现，区间加操作就转化为了差分数组两端点的修改。

除此之外，最大公约数还满足以下性质：

  1. 。

也就是说上传操作时当前区间的最大公约数就应该是左右子树二者的最大公约数的最大公约数，叶子节点的最大公约数应是它自身的值。同样的，多个数求最大公约数也可以转化为两两求解最大公约数。

总结：对于一个数列 ，它的差分数组为 ，那么数列 所有元素的最大公约数应是 。因此需要额外知道查询区间的左端点值，差分数组的前缀和即为单点值，于是再维护一个区间和即可完成。同上面那道题一样，修改左右端点时需注意边界。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>
#define N 500010
using namespace std;

typedef long long ll;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    ll sum, gcd;
} tree[N << 2];
ll a[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
    tree[idx].gcd = gcd(leftSubtree(idx).gcd, rightSubtree(idx).gcd);
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) {
        tree[idx].sum = tree[idx].gcd = a[l] - a[l - 1];
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int uid, ll x) {
    if (tree[idx].size == 1 && tree[idx].l == uid) {
        tree[idx].sum += x;
        tree[idx].gcd += x;
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (uid <= mid) modify(le(idx), uid, x);
    if (uid > mid) modify(ri(idx), uid, x);
    pushup(idx);
}

ll querySum(int idx, int r) {
    if (tree[idx].r <= r) return tree[idx].sum;
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    ll ret = 0;
    ret += querySum(le(idx), r);
    if (r > mid) ret += querySum(ri(idx), r);
    return ret;
}

ll queryGcd(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].gcd;
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    ll ret = 0;
    if (l <= mid) ret = gcd(ret, queryGcd(le(idx), l, r));
    if (r > mid) ret = gcd(ret, queryGcd(ri(idx), l, r));
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    while (m--) {
        char op;
        int l, r;
        cin >> op >> l >> r;
        if (op == 'C') {
            ll x;
            cin >> x;
            modify(1, l, x);
            if (r < n) modify(1, r + 1, -x);
        } else cout << abs(gcd(querySum(1, l), queryGcd(1, l + 1, r))) << endl; // 注意取绝对值
    }

    return 0;
}

较复杂的序列操作

数据结构维护序列也是常考的一个点，维护二进制序列的各种操作又从中脱颖而出。由于操作的复杂性，它们有时还会涉及到多重懒标记的下传优先级和清空问题。本节重点在讲解一些序列上的经典操作的维护。

非空最大子段和

例题：GSS1 - Can you answer these queries I（单点带修请见 GSS3，维护思路完全相同）

难度：提高+/省选-

维护变量：最大前缀、最大后缀、最大子段和、区间和。

维护最大子段和考虑三种情况：

  1. 最大子段和为左侧的最大子段和
  2. 最大子段和为右侧的最大子段和
  3. 最大子段和跨区间，为左区间的最大后缀加右区间的最大前缀

最大子段和就是上述三种情况的最大值。

维护最大前缀考虑两种情况（最大后缀同理）：

  1. 最大前缀为左区间的最大前缀
  2. 最大前缀跨区间，为整个左区间和右区间的最大前缀之和

最大前/后缀就是上述两种情况的最大值。

注意选取的子段中必须包含至少一个元素（即非空最大子段和），否则不可用这种方式做。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <bits/stdc++.h>
#define N 50010
using namespace std;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(idx) (tree[le(idx)])
#define rightSubtree(idx) (tree[ri(idx)])
    int l, r;
    int max, lmax, rmax;
    int sum;
} tree[N << 2];

int a[N];

void pushup(int idx) {
    tree[idx].max = max(max(leftSubtree(idx).max, rightSubtree(idx).max), leftSubtree(idx).rmax + rightSubtree(idx).lmax);
    tree[idx].lmax = max(leftSubtree(idx).lmax, leftSubtree(idx).sum + rightSubtree(idx).lmax);
    tree[idx].rmax = max(rightSubtree(idx).rmax, rightSubtree(idx).sum + leftSubtree(idx).rmax);
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    if (l == r) {
        tree[idx].max = a[l];
        tree[idx].lmax = a[l];
        tree[idx].rmax = a[l];
        tree[idx].sum = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

SegmentTree query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx];
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l > mid) return query(ri(idx), l, r);
    if (r <= mid) return query(le(idx), l, r);
    SegmentTree L{}, R{}, res{};
    L = query(le(idx), l, r);
    R = query(ri(idx), l, r);
    res.max = max(max(L.max, R.max), L.rmax + R.lmax);
    res.lmax = max(L.lmax, L.sum + R.lmax);
    res.rmax = max(R.rmax, R.sum + L.rmax);
    res.sum = L.sum + R.sum;
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    cin >> m;
    while (m--) {
        int l, r;
        cin >> l >> r;
        cout << query(1, l, r).max << endl;
    }
    return 0;
}

有端点限制的最大子段和

例题：GSS5 - Can you answer these queries V

难度：省选/NOI-

只要解决了端点问题它就变成 GSS1 了！——这不废话吗？

对于左右端点所在区间的位置情况进行讨论。

第一种，两端点区间无交集。那么两区间中间的区域是一定要选的，我们加上这一段的总和，然后合并左端点区间的最大后缀、右端点区间的最大前缀即可。

第二种，两区间有交集。它又可以分三类讨论，如下图：

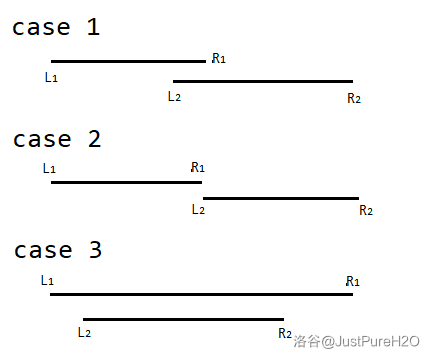
发现三种位置关系可以用一个方法得到答案，讨论答案区间左右端点的分布：左右端点可能的分布是 、，此时答案是前者最大后缀与后者最大前缀的和；或者是同属于 ，答案是这个区间的最大子段和（简化为 GSS1）；也可能是 、，答案是前者最大后缀与后者最大前缀的和。最终就是三种情况取最大值。

为了减少特判，我们规定当查询的左边界大于右边界时即返回 ；为了避免区间求值出现端点重合而重复计算的情况，我们在最后减去重合端点的单点值（毕竟不带修）即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>

#define N 100010
using namespace std;

typedef long long ll;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    ll sum;
    ll max[3];
} tree[N << 2];
int a[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
    tree[idx].max[0] = max(leftSubtree(idx).max[0], leftSubtree(idx).sum + rightSubtree(idx).max[0]);
    tree[idx].max[1] = max(rightSubtree(idx).max[1], rightSubtree(idx).sum + leftSubtree(idx).max[1]);
    tree[idx].max[2] = max(
            {leftSubtree(idx).max[2], rightSubtree(idx).max[2], leftSubtree(idx).max[1] + rightSubtree(idx).max[0]});
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) {
        tree[idx].sum = a[l];
        tree[idx].max[0] = tree[idx].max[1] = tree[idx].max[2] = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

ll querySum(int idx, int l, int r) {
    if (l > r) return 0;
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum;
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    ll ret = 0;
    if (l <= mid) ret += querySum(le(idx), l, r);
    if (r > mid) ret += querySum(ri(idx), l, r);
    return ret;
}

SegmentTree query(int idx, int l, int r) {
    if (l > r) return {0, 0, 0, 0, 0, 0, 0};
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx];
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l > mid) return query(ri(idx), l, r);
    if (r <= mid) return query(le(idx), l, r);
    SegmentTree L = query(le(idx), l, r);
    SegmentTree R = query(ri(idx), l, r);
    SegmentTree res{};
    res.sum = L.sum + R.sum;
    res.max[0] = max(L.max[0], L.sum + R.max[0]);
    res.max[1] = max(R.max[1], R.sum + L.max[1]);
    res.max[2] = max({L.max[2], R.max[2], L.max[1] + R.max[0]});
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int t;
    cin >> t;
    while (t--) {
        int n, m;
        cin >> n;
        for (int i = 1; i <= n; i++) cin >> a[i];
        build(1, 1, n);
        cin >> m;
        while (m--) {
            int l1, r1, l2, r2;
            cin >> l1 >> r1 >> l2 >> r2;
            if (r1 < l2)
                cout << query(1, l1, r1).max[1] + querySum(1, r1, l2) + query(1, l2, r2).max[0] - a[r1] - a[l2] << endl;
            else
                cout << max({query(1, l2, r1).max[2], query(1, l1, r1).max[1] + query(1, r1, r2).max[0] - a[r1],
                             query(1, l1, l2).max[1] +
                             query(1, l2, r2).max[0] - a[l2]}) << endl;
        }
    }

    return 0;
}

实数域上整数端点的集合运算

例题：P5568 [SDOI2008] 校门外的区间

难度：提高+/省选-

来源：山东  2008

维护变量：区间和、0/1推平标记、异或标记

考虑维护一个 0/1 串，记录集合中是否有对应位置的数。对于求并操作，相当于把读入的目标区间和集合的对应位置进行按位或运算，又因为读入的区间必定是全为 1 的表示，因此可以看作区间内推平为 1；对于求交操作，则是相当于按位与运算，且目标区间外需均推平为 0，而这对集合的对应区间无影响，综合来说就是区间外推平为 0。

然后再来考虑两种减法操作。对于原集合和目标区间的相对差集（操作 ），相当于原集合减去二者的交集，那么就是目标区间内推平为 0；而对于目标区间和原集合的相对差集（操作 ）就稍微复杂一些了，原理如下图：

相当于用目标区间减去二者交集。可以发现我们只要目标区间有但是集合里没有的元素，那么目标区间外可以推平为 0。此时再让集合中有的数变没，再让没有的数出现，不难想到异或（按位 0/1 翻转）。综上，需要区间外推平为 0，再区间内异或；对于最后一个求对称差的操作，从符号可知 仔细研究规则即可发现就是区间内异或。

维护两种标记时要额外注意优先级问题。比较优先级时常用假设当前区间存在其他标记的方法来推理。当推平操作下发到一个已有异或标记的区间时，无论异或结果如何都不会改变推平的事实，可知推平标记优先级大于异或标记。当然这不代表要在区间推平下传结束后一并清空区间异或标记，详见前文提到的“标记置零问题”。

最后是处理输入输出的开闭区间。可以把原始下标都翻倍，闭区间端点的下标是偶数，开区间就是奇数。输出时可以暴力统计前缀和，然后处理出连续区间，根据下标奇偶性即可推知答案区间的开闭，再减半取整输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
#include <bits/stdc++.h>
#define N 140000
#define UNION 1
#define INTERSECT 2
#define XOR 3
using namespace std;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    int sum = 0;
    bool flagXor;
    int flagRev;
} tree[N << 2];
int tmp[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
}

void pushdown(int idx) {
    if (tree[idx].flagRev != -1) {
        leftSubtree(idx).flagXor = false;
        leftSubtree(idx).flagRev = tree[idx].flagRev;
        leftSubtree(idx).sum = leftSubtree(idx).size * tree[idx].flagRev;
        rightSubtree(idx).flagXor = false;
        rightSubtree(idx).flagRev = tree[idx].flagRev;
        rightSubtree(idx).sum = rightSubtree(idx).size * tree[idx].flagRev;
        tree[idx].flagRev = -1;
    }
    if (tree[idx].flagXor) {
        leftSubtree(idx).flagXor ^= true;
        leftSubtree(idx).sum = leftSubtree(idx).size - leftSubtree(idx).sum;
        rightSubtree(idx).flagXor ^= true;
        rightSubtree(idx).sum = rightSubtree(idx).size - rightSubtree(idx).sum;
        tree[idx].flagXor = false;
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    tree[idx].flagRev = -1;
    if (l == r) return;
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, int type) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        if (type == UNION) {
            // 区间推平成1
            tree[idx].flagRev = 1;
            tree[idx].flagXor = false;
            tree[idx].sum = tree[idx].size;
        } else if (type == XOR) {
            // 异或
            tree[idx].flagXor ^= true;
            tree[idx].sum = tree[idx].size - tree[idx].sum;
        } else if (type == INTERSECT) {
            // 区间推平为0
            tree[idx].flagRev = 0;
            tree[idx].flagXor = false;
            tree[idx].sum = 0;
        }
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, type);
    if (r > mid) modify(ri(idx), l, r, type);
    pushup(idx);
}

int query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum;
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    int ret = 0;
    if (l <= mid) ret += query(le(idx), l, r);
    if (r > mid) ret += query(ri(idx), l, r);
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    char op, lpath, comma, rpath;
    int a, b, R = 0;
    build(1, 0, 65535 << 1);
    while (cin >> op) {
        cin >> lpath >> a >> comma >> b >> rpath;
        a <<= 1, b <<= 1;
        if (lpath == '(') a++;
        if (rpath == ')') b--;
        if (b < a) continue;
        R = max(R, b); // 记录最大右端点
        switch (op) {
            case 'U': // 并集 目标区间内推平为1
                modify(1, a, b, UNION);
                break;
            case 'D': // 相对差集 目标区间内推平为0
                modify(1, a, b, INTERSECT);
                break;
            case 'I': // 交集 目标区间外推平为0
                if (a) modify(1, 0, a - 1, INTERSECT);
                if (b < 65535 << 1) modify(1, b + 1, 65535 << 1, INTERSECT);
                break;
            case 'C': // 逆相对差集 目标区间内异或，且区间外推平为0
                modify(1, a, b, XOR);
                if (a) modify(1, 0, a - 1, INTERSECT);
                if (b < 65535 << 1) modify(1, b + 1, 65535 << 1, INTERSECT);
                break;
            case 'S': // 对称差 目标区间内异或
            default:
                modify(1, a, b, XOR);
                break;
        }
    }
    int t = query(1, 0, R); // 检查前缀和，为 0 则为空集
    if (!t) cout << "empty set" << endl; 
    else {
        for (int i = 0; i <= R + 2; i++) tmp[i] = query(1, 0, i); // 前缀和
        int last = 0, lastI = -2;
        for (int i = 0; i <= R; i++) {
            if (tmp[i] - last) {
                if (i - lastI > 1) cout << (i & 1 ? '(' : '[') << (i >> 1) << ','; // 根据奇偶性判断括号
                if (tmp[i + 1] == tmp[i]) cout << (i + 1 >> 1) << (i & 1 ? ')' : ']') << ' ';
                last = tmp[i];
                lastI = i;
            }
        }
    }

    return 0;
}

区间推平+区间翻转+最大连续数（01串）

例题：P2572 序列操作

题目难度：提高+/省选-

题目来源：四川  2010  各省省选

维护变量：区间左端最大连续数、区间右端最大连续数、区间最大连续数、区间大小、区间和

最大连续数考虑三种情况：

  1. 左区间最大连续数
  2. 右区间最大连续数
  3. 跨区间，左区间右端最大连续数与右区间左端最大连续数

最大左端连续数（右端同理）考虑两种情况：

  1. 不可跨区间，为左区间最大左端连续数
  2. 可以跨区间（左区间均为同一个数），那么为左区间最大左端连续数与右区间最大左端连续数之和

标记优先级推平大于翻转。注意当前区间如果已经存在一个推平标记，那么下传翻转标记时就需要把推平标记取反。推平后相应数字的最大连续数均设置成区间长度、另一个数字的最大连续数设为 ，此时的区间的和就是该区间的长度减去先前记录的区间和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
#include <bits/stdc++.h>
#define N 100010
using namespace std;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(idx) (tree[le(idx)])
#define rightSubtree(idx) (tree[ri(idx)])
    int l, r;
    int que, rev;
    int lmax[2], rmax[2], max[2];
    int sum, size;
} tree[N << 2];

int a[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
    for (int i = 0; i <= 1; i++) {
        tree[idx].max[i] = max(max(leftSubtree(idx).max[i], rightSubtree(idx).max[i]), leftSubtree(idx).rmax[i] + rightSubtree(idx).lmax[i]); // 最大连续数的三种情况
        tree[idx].lmax[i] = leftSubtree(idx).lmax[i]; // 左端最大连续为左子树的左端最大连续
        if (leftSubtree(idx).sum == i * leftSubtree(idx).size) tree[idx].lmax[i] += rightSubtree(idx).lmax[i]; // 可以跨区间，加入右子树的左端最大连续
        tree[idx].rmax[i] = rightSubtree(idx).rmax[i]; // 右端最大连续为右子树的右端最大连续
        if (rightSubtree(idx).sum == i * rightSubtree(idx).size) tree[idx].rmax[i] += leftSubtree(idx).rmax[i]; // 可以跨区间，加入左子树的右端最大连续
    }
}

void pushdown(int idx) {
    if (tree[idx].que >= 0) {
        int tag = tree[idx].que; // 下传推平标记
        leftSubtree(idx).lmax[tag] = leftSubtree(idx).rmax[tag] = leftSubtree(idx).max[tag] = leftSubtree(idx).size; // 推平的那个数的最大连续均变为子树大小
        rightSubtree(idx).lmax[tag] = rightSubtree(idx).rmax[tag] = rightSubtree(idx).max[tag] = rightSubtree(idx).size;
        leftSubtree(idx).lmax[tag ^ 1] = leftSubtree(idx).rmax[tag ^ 1] = leftSubtree(idx).max[tag ^ 1] = 0; // 反之，另一个数的最大连续均变为0
        rightSubtree(idx).lmax[tag ^ 1] = rightSubtree(idx).rmax[tag ^ 1] = rightSubtree(idx).max[tag ^ 1] = 0;

        leftSubtree(idx).sum = leftSubtree(idx).size * tag; // 维护和
        rightSubtree(idx).sum = rightSubtree(idx).size * tag;

        leftSubtree(idx).que = tag;
        leftSubtree(idx).rev = 0;
        rightSubtree(idx).que = tag;
        rightSubtree(idx).rev = 0;
        tree[idx].que = -1;
        tree[idx].rev = 0;
    }
    if (tree[idx].rev) {
        leftSubtree(idx).sum = leftSubtree(idx).size - leftSubtree(idx).sum;
        rightSubtree(idx).sum = rightSubtree(idx).size - rightSubtree(idx).sum;
        swap(leftSubtree(idx).lmax[0], leftSubtree(idx).lmax[1]); // 0/1互换，最大连续也互换
        swap(leftSubtree(idx).rmax[0], leftSubtree(idx).rmax[1]);
        swap(leftSubtree(idx).max[0], leftSubtree(idx).max[1]);
        swap(rightSubtree(idx).lmax[0], rightSubtree(idx).lmax[1]);
        swap(rightSubtree(idx).rmax[0], rightSubtree(idx).rmax[1]);
        swap(rightSubtree(idx).max[0], rightSubtree(idx).max[1]);

        if (leftSubtree(idx).que >= 0) leftSubtree(idx).que ^= 1; // 如果先有了推平，那么相当于推平成另一个数
        else leftSubtree(idx).rev ^= 1;
        if (rightSubtree(idx).que >= 0) rightSubtree(idx).que ^= 1;
        else rightSubtree(idx).rev ^= 1;

        tree[idx].rev = 0;
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    tree[idx].que = -1;
    if (l == r) {
        tree[idx].sum = a[l];
        tree[idx].lmax[a[l]] = tree[idx].rmax[a[l]] = tree[idx].max[a[l]] = 1;
        tree[idx].lmax[a[l] ^ 1] = tree[idx].rmax[a[l] ^ 1] = tree[idx].max[a[l] ^ 1] = 0;
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, int x) {
    pushdown(idx);
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].sum = x * tree[idx].size;
        tree[idx].que = x;
        tree[idx].lmax[x] = tree[idx].rmax[x] = tree[idx].max[x] = tree[idx].size;
        tree[idx].lmax[x ^ 1] = tree[idx].rmax[x ^ 1] = tree[idx].max[x ^ 1] = 0;
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

void reverse(int idx, int l, int r) {
    pushdown(idx);
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].sum = tree[idx].size - tree[idx].sum;
        tree[idx].rev ^= 1;
        swap(tree[idx].lmax[0], tree[idx].lmax[1]);
        swap(tree[idx].rmax[0], tree[idx].rmax[1]);
        swap(tree[idx].max[0], tree[idx].max[1]);
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) reverse(le(idx), l, r);
    if (r > mid) reverse(ri(idx), l, r);
    pushup(idx);
}

int queryTotal(int idx, int l, int r) {
    pushdown(idx);
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum;
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    int res = 0;
    if (l <= mid) res += queryTotal(le(idx), l, r);
    if (r > mid) res += queryTotal(ri(idx), l, r);
    return res;
}

SegmentTree queryMax(int idx, int l, int r) {
    pushdown(idx);
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx];
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l > mid) return queryMax(ri(idx), l, r);
    if (r <= mid) return queryMax(le(idx), l, r);
    SegmentTree L{}, R{}, res{};
    L = queryMax(le(idx), l, r);
    R = queryMax(ri(idx), l, r);
    for (int i = 0; i <= 1; i++) {
        res.max[i] = max(max(L.max[i], R.max[i]), L.rmax[i] + R.lmax[i]);
        res.lmax[i] = L.lmax[i];
        if (L.sum == i * L.size) res.lmax[i] += R.lmax[i];
        res.rmax[i] = R.rmax[i];
        if (R.sum == i * R.size) res.rmax[i] += L.rmax[i];
    }
    res.sum = L.sum + R.sum;
    res.size = L.size + R.size;
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    while (m--) {
        int op, x, y;
        cin >> op >> x >> y;
        x++, y++; // 勿删！
        if (op == 0) modify(1, x, y, 0);
        else if (op == 1) modify(1, x, y, 1);
        else if (op == 2) reverse(1, x, y);
        else if (op == 3) cout << queryTotal(1, x, y) << endl;
        else cout << queryMax(1, x, y).max[1] << endl;
    }
    return 0;
}

维护数学运算

针对区间待修和区间查询的问题， 我们一般会首先想到线段树，在一些区间数学操作的题目中也不例外。尽管这些数学运算并不一定具备结合律，有时我们仍然可以通过它们的其他性质（短时性，不会进行太多次操作就会变为可做的形式）来转化为简单维护问题去解决。本节就精选了一些线段树维护数学运算的例子。

区间开方+区间和

例题：GSS4 - Can you answer these queries IV

题目难度：提高+/省选-

维护变量： 区间和、区间开方判别标记

由于平方根下求和没有计算公式，但是考虑到像 这样的大数据，在经过 次开方后都会变成 ，而 。这就是开方运算的短时性。它启发我们把区间修改变为暴力单点修改，记录一下当前数开方后是否等于 或 ，如果是则给它做一个标记、并向上更新标记。如果区间被标记，更改时则无需递归进去，简化了大量操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <bits/stdc++.h>
#define N 100010
using namespace std;

typedef long long ll;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(idx) (tree[le(idx)])
#define rightSubtree(idx) (tree[ri(idx)])
    int l, r;
    ll sum;
} tree[N << 2];

ll a[N];

inline void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    if (l == r) {
        tree[idx].sum = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

inline void modify(int idx, int l, int r) {
    if (tree[idx].sum <= tree[idx].r - tree[idx].l + 1) return; // 已经全为 0/1，开方后不变
    if (tree[idx].l == tree[idx].r) {
        tree[idx].sum = static_cast<ll>(sqrt(tree[idx].sum)); // 否则暴力单点修改
        return;
    }
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r);
    if (r > mid) modify(ri(idx), l, r);
    pushup(idx);
}

inline ll query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum;
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    ll res = 0;
    if (l <= mid) res += query(le(idx), l, r);
    if (r > mid) res += query(ri(idx), l, r);
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, c = 0;
    while (cin >> n) {
        memset(tree, 0, sizeof tree);
        memset(a, 0, sizeof a);
        for (int i = 1; i <= n; i++) cin >> a[i];
        build(1, 1, n);

        cout << "Case #" << ++c << ":\n";
        int q;
        cin >> q;
        while (q--) {
            int op, x, y;
            cin >> op >> x >> y;
            if (x > y) swap(x, y);
            if (op == 0) modify(1, x, y);
            else cout << query(1, x, y) << '\n';
        }
        cout << '\n';
    }
    return 0;
}

区间加+区间sin和

例题：P6327 区间加区间 sin 和

题目难度：提高+/省选-

维护变量：区间 和、区间 和、角度加法懒标记

正余弦函数显然具备结合律。根据正弦值的和角公式：，这里维护一个加法懒标记，在下传时使用和角公式一次性计算、同时维护 和即可。注意需要把相关 和 值存成变量再更新，否则答案错误（这样连样例都能过）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#include <bits/stdc++.h>
#define N 200010
using namespace std;

const double EPS = 1e-8;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    double sin, cos;
    double lazy;
} tree[N << 2];
double a[N];

void pushup(int idx) {
    tree[idx].sin = leftSubtree(idx).sin + rightSubtree(idx).sin;
    tree[idx].cos = leftSubtree(idx).cos + rightSubtree(idx).cos;
}

void pushdown(int idx) {
    if (abs(tree[idx].lazy) > EPS) {
        double SIN = sin(tree[idx].lazy), COS = cos(tree[idx].lazy); // 需要先存成变量，否则变量中途修改会影响其他变量
        double LSIN = leftSubtree(idx).sin, LCOS = leftSubtree(idx).cos;
        double RSIN = rightSubtree(idx).sin, RCOS = rightSubtree(idx).cos;

        leftSubtree(idx).sin = SIN * LCOS + COS * LSIN; // sin 和角公式
        leftSubtree(idx).cos = COS * LCOS - SIN * LSIN; // cos 和角公式
        leftSubtree(idx).lazy += tree[idx].lazy;
        rightSubtree(idx).sin = SIN * RCOS + COS * RSIN;
        rightSubtree(idx).cos = COS * RCOS - SIN * RSIN;
        rightSubtree(idx).lazy += tree[idx].lazy;

        tree[idx].lazy = 0.0;
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    tree[idx].lazy = 0.0;
    if (l == r) {
        tree[idx].sin = sin(a[l]);
        tree[idx].cos = cos(a[l]);
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, double x) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        double SIN = tree[idx].sin, COS = tree[idx].cos; // 同理，需要预先存成变量
        double SINX = sin(x), COSX = cos(x);
        tree[idx].sin = SIN * COSX + COS * SINX;
        tree[idx].cos = COS * COSX - SIN * SINX;
        tree[idx].lazy += x;
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

double query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sin;
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    double ret = 0.0;
    if (l <= mid) ret += query(le(idx), l, r);
    if (r > mid) ret += query(ri(idx), l, r);
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    cin >> m;
    while (m--) {
        int op, l, r;
        double v;
        cin >> op >> l >> r;
        if (op == 1) {
            cin >> v;
            modify(1, l, r, v);
        } else cout << fixed << setprecision(1) << query(1, l, r) << endl;
    }

    return 0;
}

区间加+区间平均数+区间方差

例题：P1471 方差

题目难度：提高+/省选-

维护变量：区间平方和、区间和

方差公式：，展开化简得 。因此维护平方和用于计算分数部分。进行区间加时，维护平方和有这个公式：。具备结合律。我们按照公式维护即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include <bits/stdc++.h>
#define N 100010
using namespace std;

typedef long long ll;

const double EPS = 1e-8;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    double sum, sumSq;
    double lazy, lazySq;
} tree[N << 2];
double a[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
    tree[idx].sumSq = leftSubtree(idx).sumSq + rightSubtree(idx).sumSq;
}

void pushdown(int idx) {
    if (abs(tree[idx].lazySq) > EPS) {
        leftSubtree(idx).sumSq += 2 * leftSubtree(idx).sum * tree[idx].lazySq + leftSubtree(idx).size * tree[idx].lazySq * tree[idx].lazySq;
        leftSubtree(idx).lazySq += tree[idx].lazySq;
        rightSubtree(idx).sumSq += 2 * rightSubtree(idx).sum * tree[idx].lazySq + rightSubtree(idx).size * tree[idx].lazySq * tree[idx].lazySq;
        rightSubtree(idx).lazySq += tree[idx].lazySq;
        tree[idx].lazySq = 0;
    }
    if (abs(tree[idx].lazy) > EPS) {
        leftSubtree(idx).sum += leftSubtree(idx).size * tree[idx].lazy;
        leftSubtree(idx).lazy += tree[idx].lazy;
        rightSubtree(idx).sum += rightSubtree(idx).size * tree[idx].lazy;
        rightSubtree(idx).lazy += tree[idx].lazy;
        tree[idx].lazy = 0;
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) {
        tree[idx].sum = a[l];
        tree[idx].sumSq = a[l] * a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, double x) {
    if(l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].sumSq += 2 * tree[idx].sum * x + tree[idx].size * x * x;
        tree[idx].lazySq += x;
        tree[idx].sum += x * tree[idx].size;
        tree[idx].lazy += x;
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

double querySum(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum;
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    double ret = 0.0;
    if (l <= mid) ret += querySum(le(idx), l, r);
    if (r > mid) ret += querySum(ri(idx), l, r);
    return ret;
}

double querySumSq(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sumSq;
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    double ret = 0.0;
    if (l <= mid) ret += querySumSq(le(idx), l, r);
    if (r > mid) ret += querySumSq(ri(idx), l, r);
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    while (m--) {
        int op, l, r;
        double x;
        cin >> op >> l >> r;
        int size = r - l + 1;
        if (op == 1) {
            cin >> x;
            modify(1, l, r, x);
        } else if (op == 2) cout << fixed << setprecision(4) << querySum(1, l, r) / size << endl;
        else cout << fixed << setprecision(4) << querySumSq(1, l, r) / size - pow(querySum(1, l, r) / size, 2) << endl;
    }

    return 0;
}

维护历史最值/历史操作

提到历史操作，我们可能会想到线段树家族的一个分支——可持久化线段树/主席树（或者是吉司机线段树），它通过复制修改时经过的相关节点来实现对某一历史操作的高效维护，更为详细的内容见此。一般来说，涉及到历史最值的线段树都需要在平常维护的普通标记上分别新增一个历史最值标记，进而可能涉及到众多懒标记的维护，因此懒标记之间的维护优先级（分类讨论）也是必须弄清的一大重点。

多标记维护有一个很明显的缺点是分类讨论繁杂、码量膨胀迅速。事实上，除了多标记硬维护，我们还可以稍稍更改矩阵乘法的定义，使用广义矩阵乘法来解决历史最值问题。如果对矩阵乘法不太了解的请左转 矩阵乘法相关，对矩阵构造不太了解的请右转 初等矩阵与矩阵递推。

多标记历史最值

例题：P4314 CPU 监控

难度：省选/NOI-

维护变量：区间加懒标记、区间推平懒标记、区间推平存在性标记、区间历史最大加法懒标记、区间历史最大推平懒标记

简化题意。：查询区间最大值；：查询区间曾经出现过的所有值的最大值；：区间加；：区间推平。

首先，维护区间加和区间推平标记是必须的。注意到，在某一次进行了一次推平操作，后到的区间加本质上就是区间推平（即区间推平优先级高于区间加）。我们其实只需考虑首次区间推平前的所有区间加操作与它之间的关系。总而言之，对于一段区间的所有操作，我们都可以把它简化成一次区间加法后接一次区间推平。

根据优先级关系可得：如果之前已经对区间进行过推平，且当前要对这个区间进行区间加，那么我们就把区间加变成区间推平，只不过推平的数是原来的数加上区间加的操作数。否则就正常执行区间加。这里我们使用一个推平存在性标记来区分曾经执行过推平的区间和没执行过推平的区间。

接下来是重点，我们要更新历史最值的标记。对于推平操作，如果曾经推平过，就是原先的历史最大值与推平数取最大值、否则标记当前区间为存在过推平，且把历史最大值赋值成操作数；对于区间加，如果存在推平则转化为推平、否则历史标记更新为当前区间的历史标记与操作数总和的最大值。然后是正常加法标记、推平标记和区间最大值的更新，不要忘了用历史值更新当前历史最大值。

这里使用了复杂查询，其实可以只用简单查询，但是这样会让一个函数变成两个函数，比较占用篇幅。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <bits/stdc++.h>

#define N 100010
#define ADD 0
#define COV 1
using namespace std;

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    bool flag_cov;
    int lazy_add, lazy_cov, h_lazy_add, h_lazy_cov;
    int max, hmax;

    void cover(int x, int hx) {
        if (flag_cov) h_lazy_cov = std::max(h_lazy_cov, hx); // 存在推平
        else flag_cov = true, h_lazy_cov = hx; // 不存在推平，标记并更新
        hmax = std::max(hmax, hx);
        max = x;
        lazy_cov = x;
        lazy_add = 0;
    }

    void add(int x, int hx) {
        if (flag_cov) cover(lazy_cov + x, lazy_cov + hx); // 存在推平，转化为推平
        else {
            h_lazy_add = std::max(h_lazy_add, lazy_add + hx); // 正常维护区间加法
            hmax = std::max(hmax, max + hx);
            lazy_add += x;
            max += x;
        }
    }
} tree[N << 2];

int a[N];

void pushup(int idx) {
    tree[idx].max = max(leftSubtree(idx).max, rightSubtree(idx).max);
    tree[idx].hmax = max(leftSubtree(idx).hmax, rightSubtree(idx).hmax);
}

void pushdown(int idx) {
    if (tree[idx].lazy_add || tree[idx].h_lazy_add) {
        leftSubtree(idx).add(tree[idx].lazy_add, tree[idx].h_lazy_add);
        rightSubtree(idx).add(tree[idx].lazy_add, tree[idx].h_lazy_add);
        tree[idx].lazy_add = tree[idx].h_lazy_add = 0;
    }
    if (tree[idx].flag_cov) {
        leftSubtree(idx).cover(tree[idx].lazy_cov, tree[idx].h_lazy_cov);
        rightSubtree(idx).cover(tree[idx].lazy_cov, tree[idx].h_lazy_cov);
        tree[idx].lazy_cov = tree[idx].h_lazy_cov = 0;
        tree[idx].flag_cov = false;
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    tree[idx].max = tree[idx].hmax = -INT_MAX;
    if (l == r) {
        tree[idx].max = tree[idx].hmax = a[l];
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, int x, int type) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        if (type == COV) tree[idx].cover(x, x);
        else if (type == ADD) tree[idx].add(x, x);
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x, type);
    if (r > mid) modify(ri(idx), l, r, x, type);
    pushup(idx);
}

SegmentTree query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx];
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l > mid) return query(ri(idx), l, r);
    if (r <= mid) return query(le(idx), l, r);
    SegmentTree L = query(le(idx), l, r);
    SegmentTree R = query(ri(idx), l, r);
    SegmentTree res{};
    res.l = L.l, res.r = R.r, res.size = L.size + R.size;
    res.max = max(L.max, R.max), res.hmax = max(L.hmax, R.hmax);
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    cin >> m;
    while (m--) {
        char op;
        int l, r, x;
        cin >> op >> l >> r;
        if (op == 'Q') cout << query(1, l, r).max << endl;
        else if (op == 'A') cout << query(1, l, r).hmax << endl;
        else if (op == 'P') {
            cin >> x;
            modify(1, l, r, x, ADD);
        } else {
            cin >> x;
            modify(1, l, r, x, COV);
        }
    }
    return 0;
}

广义矩阵乘法历史最值

例题：P4314 CPU 监控

难度：省选/NOI-

维护变量：广义矩阵和、广义矩阵乘法标记

一题多解，多题归一

对于当前最值和历史最值组成的向量 ，我们自然希望它在操作后变成我们希望的样子，也就是变成 。一般采取的措施是重定义矩阵元素间的运算。

重定义矩阵元素间的加法为取最大值、元素间的乘法为代数加法。因此对于一段区间，和式 就同时维护了当前区间的最大值和历史最大值；乘积 维护了单点操作后的最大值和历史最大值。

在新定义下，我们需要重定义零矩阵和单位矩阵。根据定义，零矩阵乘任何矩阵都是一个零矩阵，可以构造出广义零矩阵 ；单位矩阵乘任何矩阵都是后者，因此构造广义单位矩阵 。

突然发现还有一个区间推平需要我们维护。换句话说，针对原矩阵 ，构造一个右乘矩阵使得二者乘积为 。发现似乎构造不出普通的 转移矩阵使条件成立，因此考虑升维。如果原始矩阵是 ，转移矩阵是 的话就符合要求了。相应的，区间加操作的转移矩阵需变成 。

于是我们把问题转化成了询问区间矩阵和与区间乘矩阵的问题了，只需维护区间矩阵和、乘数矩阵标记即可。需要注意的是，懒标记的初始值应为广义单位矩阵、区间和的初始值应该是广义零矩阵。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
#include <bits/stdc++.h>

#define N 100010
#define ADD 0
#define COV 1
using namespace std;

typedef long long ll;

const ll INF = 1e18;

struct Matrix {
    ll mat[3][3]{};

    void O() {
        // 广义零矩阵
        for (auto &i: mat) {
            for (ll &j: i) {
                j = -INF;
            }
        }
    }

    void I() {
        // 广义单位矩阵
        for (auto &i: mat) {
            for (ll &j: i) {
                j = -INF;
            }
        }
        mat[0][0] = mat[1][1] = mat[2][2] = 0;
    }

    bool isI() {
        // 判断是否是广义单位矩阵
        for (int i = 0; i < 3; i++) {
            for (int j = 0; j < 3; j++) {
                if (i ^ j && mat[i][j] != -INF) return false;
                if (i == j && mat[i][j]) return false;
            }
        }
        return true;
    }
};

Matrix fill(int x, int type) {
    // 根据不同操作填充对应转移矩阵
    if (type == ADD) return {{{x, x, -INF}, {-INF, 0, -INF}, {-INF, -INF, 0}}};
    return {{{-INF, -INF, -INF}, {-INF, 0, -INF}, {x, x, 0}}};
}

Matrix operator*(const Matrix &l, const Matrix &r) {
    // 广义矩阵乘法
    Matrix ret;
    ret.O();
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            for (int k = 0; k < 3; k++) {
                ret.mat[i][j] = max(ret.mat[i][j], l.mat[i][k] + r.mat[k][j]);
            }
        }
    }
    return ret;
}

Matrix operator+(const Matrix &l, const Matrix &r) {
    // 广义矩阵加法
    Matrix ret;
    ret.O();
    for (int i = 0; i < 3; i++) {
        for (int j = 0; j < 3; j++) {
            ret.mat[i][j] = max(l.mat[i][j], r.mat[i][j]);
        }
    }
    return ret;
}

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    Matrix lazy, sum;
} tree[N << 2];
int a[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
}

void pushdown(int idx) {
    if (!tree[idx].lazy.isI()) {
        // 存在标记（不为广义单位矩阵）
        leftSubtree(idx).sum = leftSubtree(idx).sum * tree[idx].lazy;
        leftSubtree(idx).lazy = leftSubtree(idx).lazy * tree[idx].lazy;
        rightSubtree(idx).sum = rightSubtree(idx).sum * tree[idx].lazy;
        rightSubtree(idx).lazy = rightSubtree(idx).lazy * tree[idx].lazy;
        tree[idx].lazy.I(); // 清空成广义单位矩阵
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    tree[idx].lazy.I(); // 特别注意标记和区间和的清空
    tree[idx].sum.O();
    if (l == r) {
        tree[idx].sum = {{{a[l], a[l], 0}, {-INF, -INF, -INF}, {-INF, -INF, -INF}}};
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, int x, int type) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].sum = tree[idx].sum * fill(x, type);
        tree[idx].lazy = tree[idx].lazy * fill(x, type);
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x, type);
    if (r > mid) modify(ri(idx), l, r, x, type);
    pushup(idx);
}

SegmentTree query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx];
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l > mid) return query(ri(idx), l, r);
    if (r <= mid) return query(le(idx), l, r);
    SegmentTree L = query(le(idx), l, r);
    SegmentTree R = query(ri(idx), l, r);
    SegmentTree res{};
    res.l = L.l, res.r = R.r, res.size = L.size + R.size;
    res.sum = L.sum + R.sum;
    return res;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    cin >> m;
    while (m--) {
        char op;
        int l, r, x;
        cin >> op >> l >> r;
        if (op == 'Q') cout << query(1, l, r).sum.mat[0][0] << endl;
        else if (op == 'A') cout << query(1, l, r).sum.mat[0][1] << endl;
        else if (op == 'P') {
            cin >> x;
            modify(1, l, r, x, ADD);
        } else {
            cin >> x;
            modify(1, l, r, x, COV);
        }
    }
    return 0;
}

维护其他结合律算符

线段树的基本操作就基于子节点向当前节点的合并更新与当前节点向子节点的递归，对于具有结合律的算符，线段树能做到很好的 维护并查询。本节将重点探讨线段树维护结合律算符的部分实例。

区间加+区间斐波那契数求和

例题：CF718C Sasha and Array

难度：省选/NOI-

维护变量： 矩阵和、 矩阵加法标记

理论基础：矩阵加速递推 斐波那契数列

我在 11 月 23 日斐波那契日写下这段线段树维护斐波那契数列的文字……

我们知道矩阵快速幂可以在 的时间复杂度内快速求出斐波那契数列第 项，那么怎么把它运用在这道题中呢？

这道题要求将区间里的每个数作为下标并获得对应的斐波那契数并对其求和，不妨把区间加运算看作将当前的节点维护的斐波那契数继续向后递推 项，思路就出来了——在线段树的每个节点上维护一个矩阵，每次更新相当于对它右乘一个转移矩阵的 次幂，求和时在矩阵间进行加法运算。可以通过维护一个懒标记实现，注意下传标记时对子树标记进行矩阵乘法运算，因而懒标记的初始值应为单位矩阵、区间和的初始值应为零矩阵。

尽管此题时限有足足五秒，但仍然卡常。建议减少取模次数、展开计算矩阵乘法。我的代码在 C++17 标准下好像最后一个点会超时，换成 C++20 或 C++23（仅 CF）就快得多了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
#include <bits/stdc++.h>

#define N 100010
#define MOD 1000000007
using namespace std;

typedef long long ll;

struct Matrix {
    ll mat[3][3]{};

    Matrix() {
        mat[1][1] = mat[1][2] = mat[2][1] = mat[2][2] = 0; // 慎用 memset
    }

    Matrix(int a, int b, int c, int d) {
        // 快速赋值
        mat[1][1] = a;
        mat[1][2] = b;
        mat[2][1] = c;
        mat[2][2] = d;
    }

    Matrix operator+(Matrix b) const {
        // 矩阵加法 对位相加
        Matrix ret;
        ret.mat[1][1] = (mat[1][1] + b.mat[1][1]) % MOD;
        ret.mat[1][2] = (mat[1][2] + b.mat[1][2]) % MOD;
        ret.mat[2][1] = (mat[2][1] + b.mat[2][1]) % MOD;
        ret.mat[2][2] = (mat[2][2] + b.mat[2][2]) % MOD;
        return ret;
    }

    Matrix operator*(Matrix b) const {
        // 矩阵乘法的展开形式
        Matrix ret;
        ret.mat[1][1] = (mat[1][1] * b.mat[1][1] + mat[1][2] * b.mat[2][1]) % MOD;
        ret.mat[1][2] = (mat[1][1] * b.mat[1][2] + mat[1][2] * b.mat[2][2]) % MOD;
        ret.mat[2][1] = (mat[2][1] * b.mat[1][1] + mat[2][2] * b.mat[1][2]) % MOD;
        ret.mat[2][2] = (mat[2][1] * b.mat[1][2] + mat[2][2] * b.mat[2][2]) % MOD;
        return ret;
    }

    Matrix operator^(ll b) const {
        // 重载异或算符实现矩阵快速幂
        Matrix ret, a = *this;
        ret.I();
        while (b) {
            if (b & 1) ret = ret * a;
            a = a * a;
            b >>= 1;
        }
        return ret;
    }

    void I() {
        // 生成单位矩阵，置零是必须的
        mat[1][2] = mat[2][1] = 0;
        mat[1][1] = mat[2][2] = 1;
    }

    bool isI() {
        return mat[1][1] == 1 && mat[1][2] == 0 && mat[2][1] == 0 && mat[2][2] == 1; // 判断是否是单位矩阵（是否存在懒标记）
    }
};

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    Matrix lazy, sum;
} tree[N << 2];

const Matrix A(1, 1, 0, 0), M(0, 1, 1, 1);
ll a[N];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
}

void pushdown(int idx) {
    if (!tree[idx].lazy.isI()) {
        leftSubtree(idx).sum = leftSubtree(idx).sum * tree[idx].lazy; // 注意是乘法
        leftSubtree(idx).lazy = leftSubtree(idx).lazy * tree[idx].lazy;

        rightSubtree(idx).sum = rightSubtree(idx).sum * tree[idx].lazy;
        rightSubtree(idx).lazy = rightSubtree(idx).lazy * tree[idx].lazy;

        tree[idx].lazy.I(); // 重置为单位矩阵
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    tree[idx].lazy.I();
    if (l == r) {
        tree[idx].sum = A * (M ^ (a[l] - 1)); // 初始值就是斐波那契数列第 a[i] 项
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, ll x) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].sum = tree[idx].sum * (M ^ x); // 向后递推 x 项
        tree[idx].lazy = tree[idx].lazy * (M ^ x);
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

Matrix query(int idx, int l, int r) {
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum;
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    Matrix ret;
    if (l <= mid) ret = ret + query(le(idx), l, r);
    if (r > mid) ret = ret + query(ri(idx), l, r);
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;

    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    while (m--) {
        int op, l, r;
        cin >> op >> l >> r;
        if (op == 1) {
            ll x;
            cin >> x;
            modify(1, l, r, x);
        } else cout << query(1, l, r).mat[1][1] << endl;
    }

    return 0;
}

线段树二分

有时我们会遇到二分和线段树结合起来的题。如果使用二分区间加区间查询的方案，其时间复杂度将是 ，在 的时候会超时。此时可以借助线段树的有序性，在线段树上二分。

例题：P11217 youyou 的垃圾桶

题目难度：普及+/提高

维护变量：区间和、区间加标记

我们知道线段树可以维护一段连续的区间，这意味着我们可以在上面二分一个具有单调性的值。在线段树的最底层，从左到右分别就对应着原序列从左到右的元素。当我们需要对某个区间进行二分时，转换到树上就是看左右子树——若左子树的总和仍小于查询值，那么就在右子树查找原值减去左子树总和的值即可；否则就转到左子树找查询值。可以发现，这个逻辑和平衡树根据排名查询对应值是一样的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include <bits/stdc++.h>
#define N 200010
using namespace std;

typedef long long ll;

int a[N];

struct SegmentTree {
#define le(idx) (idx << 1)
#define ri(idx) (idx << 1 | 1)
#define leftSubtree(idx) (tree[le(idx)])
#define rightSubtree(idx) (tree[ri(idx)])
    int l, r;
    ll sum;
    ll lazy;
    int size;
} tree[N << 2];

void pushup(int idx) {
    tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;
}

void build(int idx, int l, int r) {
    tree[idx].lazy = tree[idx].sum = 0;
    tree[idx].size = r - l + 1;
    tree[idx].l = l, tree[idx].r = r;
    if (l == r) {
        tree[idx].sum = a[l];
        return;
    }
    int mid = l + r >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void pushdown(int idx) {
    if (tree[idx].lazy) {
        leftSubtree(idx).lazy += tree[idx].lazy;
        leftSubtree(idx).sum += leftSubtree(idx).size * tree[idx].lazy;
        rightSubtree(idx).lazy += tree[idx].lazy;
        rightSubtree(idx).sum += rightSubtree(idx).size * tree[idx].lazy;
        tree[idx].lazy = 0;
    }
}

void modify(int idx, int l, int r, ll x) {
    if (tree[idx].l > r || tree[idx].r < l) return;
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].sum += x * tree[idx].size;
        tree[idx].lazy += x;
        return;
    }
    pushdown(idx);
    int mid = tree[idx].l + tree[idx].r >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

ll query(int idx, int l, int r) {
    if (tree[idx].l > r || tree[idx].r < l) return 0;
    if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum;
    pushdown(idx);
    int mid = tree[idx].l + tree[idx].r >> 1;
    ll ret = 0;
    if (l <= mid) ret += query(le(idx), l, r);
    if (r > mid) ret += query(ri(idx), l, r);
    return ret;
}

int get(int idx, ll x, ll amp) {
    // 线段树二分
    if (tree[idx].l == tree[idx].r) return tree[idx].l;
    pushdown(idx);
    if (leftSubtree(idx).sum << amp >= x) return get(le(idx), x, amp);
    return get(ri(idx), x - (leftSubtree(idx).sum << amp), amp);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, q;
    ll w;
    cin >> n >> q >> w;
    for (int i = 1; i <= n; i++) cin >> a[i];
    build(1, 1, n);
    while (q--) {
        int l, r, d;
        cin >> l >> r >> d;
        modify(1, l, r, d);
        ll sum = tree[1].sum;
        ll cur = 0;
        ll k = 2, i = 1;
        for (;; i++) {
            cur += sum * (k >> 1);
            if (cur >= w) break;
            k <<= 1;
        }
        cout << n * (i - 1) + get(1, w - sum * ((k >> 1) - 1), i - 1) - 1 << '\n';
    }
    return 0;
}

例题：P11289 【MX-S6-T1】「KDOI-11」打印

题目难度：普及+/提高

维护变量：区间加标记、等待时间、区间等待时间最小值

才复习的线段树结果赛时还是没想到线段树做法

对于每个打印请求，我们预先把它们按照起始时间升序排序，然后再一个一个考虑。维护当前时间，读入到一个请求时，相当于要把当前时间后移到该请求的起始时间。此时我们让所有打印机的等待时间减去二者差值，并找出序号最小的那个打印机、更新选中打印机的等待时间、接着更新答案即可。注意等待时间最小为 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <bits/stdc++.h>
#define N 200010
using namespace std;

typedef long long ll;

struct Node {
    int id;
    ll s, t;
} nodes[N];

struct SegmentTree {
#define le(x) (x << 1)
#define ri(x) (x << 1 | 1)
#define leftSubtree(x) (tree[le(x)])
#define rightSubtree(x) (tree[ri(x)])
    int l, r, size;
    int real_id; // 记录打印机的编号
    ll time, lazy;
} tree[N << 2];

vector<int> ans[N];

bool cmp(const Node &l, const Node &r) {
    return l.t < r.t;
}

void pushup(int idx) {
    tree[idx].time = min(leftSubtree(idx).time, rightSubtree(idx).time);
}

void pushdown(int idx) {
    if (tree[idx].lazy) {
        leftSubtree(idx).time = max(0ll, leftSubtree(idx).time + tree[idx].lazy); // 等待时间不能为负
        leftSubtree(idx).lazy += tree[idx].lazy;
        rightSubtree(idx).time = max(0ll, rightSubtree(idx).time + tree[idx].lazy);
        rightSubtree(idx).lazy += tree[idx].lazy;
        tree[idx].lazy = 0;
    }
}

void build(int idx, int l, int r) {
    tree[idx].l = l, tree[idx].r = r;
    tree[idx].size = r - l + 1;
    if (l == r) {
        tree[idx].real_id = l; // 记录原始编号
        return;
    }
    int mid = (l + r) >> 1;
    build(le(idx), l, mid);
    build(ri(idx), mid + 1, r);
    pushup(idx);
}

void modify(int idx, int l, int r, ll x) {
    if (l <= tree[idx].l && tree[idx].r <= r) {
        tree[idx].lazy += x;
        tree[idx].time = max(0ll, tree[idx].time + x);
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (l <= mid) modify(le(idx), l, r, x);
    if (r > mid) modify(ri(idx), l, r, x);
    pushup(idx);
}

void modify(int idx, int uid, ll x) {
    if (tree[idx].size == 1 && tree[idx].l == uid) {
        tree[idx].time = max(0ll, tree[idx].time + x);
        return;
    }
    pushdown(idx);
    int mid = (tree[idx].l + tree[idx].r) >> 1;
    if (uid <= mid) modify(le(idx), uid, x);
    if (uid > mid) modify(ri(idx), uid, x);
    pushup(idx);
}

int find(int idx, ll time) {
    if (tree[idx].size == 1) return tree[idx].real_id; // 找到了，返回对应打印机的编号
    pushdown(idx);
    if (leftSubtree(idx).time <= time) return find(le(idx), time); // 根据建树时的编号单调性进行二分，若左侧等待时间小于等于目标，则尽量向左找
    return find(ri(idx), time); // 左侧编号更小的打印机都在工作，只能向右找空闲打印机
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int n, m;
    cin >> n >> m;
    build(1, 1, m); // 注意是 m 台打印机
    for (int i = 1; i <= n; i++) {
        cin >> nodes[i].s >> nodes[i].t;
        nodes[i].id = i;
    }
    sort(nodes + 1, nodes + 1 + n, cmp);
    ll time = 1;
    for (int i = 1; i <= n; i++) {
        modify(1, 1, m, time - nodes[i].t); // 减去时间差
        int id = find(1, tree[1].time); // 找出编号最小的空闲打印机
        ans[id].push_back(nodes[i].id); 
        modify(1, id, nodes[i].s); // 为当前打印机分配了任务，更新单点等待时间
        time = nodes[i].t; // 当前时间后移
    }
    for (int i = 1; i <= m; i++) {
        cout << ans[i].size() << ' ';
        sort(ans[i].begin(), ans[i].end());
        for (int j: ans[i]) cout << j << ' ';
        cout << endl;
    }
    return 0;
}

本页文档最后更新于：2024年11月27日

算法

oi

数据结构

评论