[熟肉] 一棵主席树新增了一个数据，这是它的结构发生的变化

标题及头图致敬油管兼B站UP主 Chubbyemu——一位非常专业的医学区博主。

可持久化简介#

可持久化数据结构，支持在保证操作不变的情况下、同时保存它的一个历史版本，以便后期的历史查询。一般的编辑器软件都会内置撤回/重做的功能，这时使用一个可持久化数据结构来存储用户的历史操作就显得非常便捷了；某些软件通过重演用户操作来实现撤回/重做功能：当用户操作较多时，会非常浪费系统资源、且效率极低，尤其是在进行连续撤回/重做时，体验感极差。

可持久化线段树/主席树理论基础#

对于一般的线段树，可以通过调用 modify 函数来进行单点插入，如果此时再加入一个要求——能够查询先前某一时刻的某一操作对应的区间最值，普通的线段树就无能为力了。比较直接的想法是：可以把每一次操作得到的线段树单独拎出来，然后对于每次询问，在对应的线段树里面跑即可。时间上过得了关，但显然这样太浪费空间——明明更改单点时只会影响到特定路径上的节点，为什么还要费劲把其他无关变量另外存下来呢？基于这个优化思路，可持久化线段树/主席树应运而生。

Tip

相关链接：可持久化线段树的发明者叫黄嘉泰，由于他和当时的国家领导人名字首字母缩写雷同，因而又叫主席树。

先来看看普通线段树的插入操作：

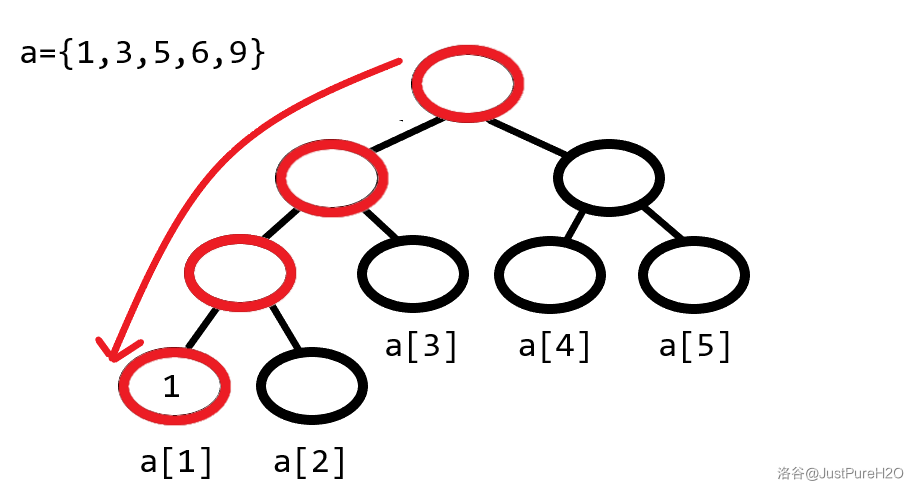
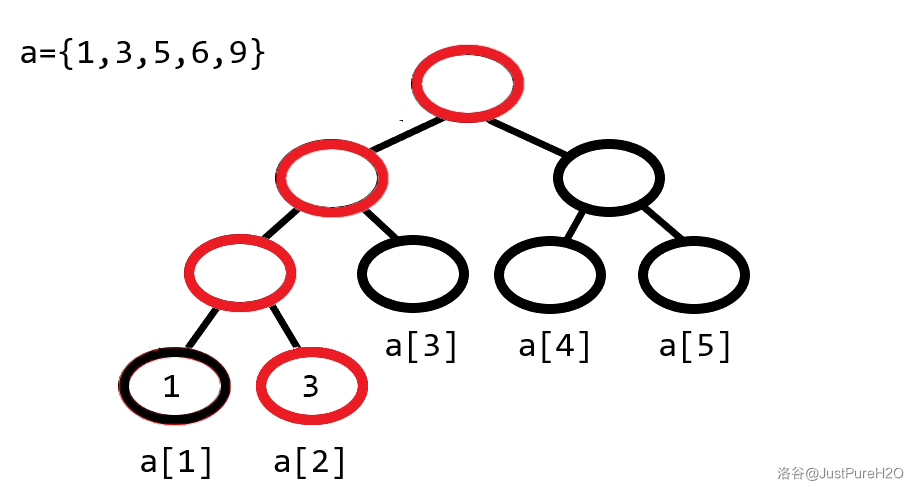
如果每次操作都要新建一整个线段树的话，那么插入五个元素的空间复杂度就有原先的五倍之多。注意到在插入操作进行时，只有红色标出的节点是受影响的，因此只需把红圈存下来而无需无效地复制那些黑色的节点。

按此理论，完成五次插入后的线段树应是下面这样（部分虚边为了美观未在图上连出）：

可以发现一个规律：副本树的连接关系与原树相同、且副本树中不连接副本节点方向上的的子树与原树对应节点的对应子树相同。但同时我们失去了一些东西——左右子树的下标再也不满足线段树中的二倍和二倍加一关系了。不过对历史记录的访问变得轻松——从右到左，分别是第一次到第五次的操作所复制出来的副本树，每个副本树都有一个根节点，代表当前的历史记录。对于询问，直接在对应根节点上查询即可。

可持久化线段树/主席树建树部分#

根据上述分析，在主席树中，把 l 和 r 变量变成节点左右子树的下标（或指针）。由于每次操作最坏会复制出一个节点数为 $\log N$ 的副本， $N$ 次修改（插入节点）之后最多同时存在 ${2N-1+N\log N}$ 个节点，习惯性把空间开到 ${32}$ 倍，也就是左移 $5$ 位。此外维护一个数组 root 用来存储每个历史记录对应的根节点：

1
struct HJTTree {
2
    int l, r;
3
    int dat; // 值
4
} tree[N << 5];
5
int idx = 0, root[N];

根据特定要求添加变量即可。在建树时，不断向深层递归，并动态创建新点。因为上面提到的主席树不再满足普通线段树的下标规律，我们给建树函数设置返回值，递归设置左右子树的值即可。大部分代码和原版线段树相差无几。

1
int build(int l, int r) {
2
    int p = ++idx; // 开点
3
    if (l == r) {
4
        tree[p].dat = a[l];
5
        return p;
6
    }
7
    int mid = (l + r) >> 1;
8
    tree[p].l = build(l, mid); // 创建左子树
9
    tree[p].r = build(mid + 1, r); // 创建右子树
10
    return p;
11
}

可持久化线段树/主席树节点插入#

插入新节点时，我们需要先把沿途的所有节点复制一遍。节点复制写在一个函数 clone(int u) 中，顾名思义，这个操作非常简单——单纯就是原先点的复制、同时返回新建的副本节点的下标。

1
int clone(int u) {
2
    int p = ++idx; // 开点
3
    tree[p] = tree[u]; // 复制
4
    return p;
5
}

接下来是节点插入的主体部分。把节点复制完毕得到一个新点后，就需要递归更新所有点的左右子树，最终在叶子节点的位置放置要插入的点。

1
int insert(int u, int dat, int pos, int l, int r) {
2
    int p = clone(u); // 先复制
3
    if (l == r) {
4
        tree[p].dat = dat; // 叶子节点的位置插入
5
        return p;
6
    }
7
    // 找到插入位置，同时更新子树
8
    int mid = (l + r) >> 1;
9
    if (pos <= mid) tree[p].l = insert(tree[u].l, dat, pos, l, mid);
10
    else tree[p].r = insert(tree[u].r, dat, pos, mid + 1, r);
11
    return p;
12
}

节点和区间的查询和普通线段树是基本一样的。这里需要注意题目要求查询哪个历史操作的值，并从相应的根节点开始向下递归查找。

模板两题#

洛谷 P3919 [模板] 可持久化线段树 1（可持久化数组）#

题目地址：P3919

题目难度：提高+/省选-

如题，你需要维护这样的一个长度为 $N$ 的数组，支持如下几种操作

在某个历史版本上修改某一个位置上的值

访问某个历史版本上的某一位置的值

此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）
输入格式：
输入的第一行包含两个正整数 $N, M$ ，分别表示数组的长度和操作的个数。
第二行包含 $N$ 个整数，依次为初始状态下数组各位的值（依次为 $a_i$ ， $1 \leq i \leq N$ ）。
接下来 $M$ 行每行包含3或4个整数，代表两种操作之一（ $i$ 为基于的历史版本号）：

对于操作1，格式为 $v_i~1~loc_i~value_i$ ，即为在版本 $v_i$ 的基础上，将 $a_{{loc}_i}$ 修改为 ${value}_i$ 。

对于操作2，格式为 $v_i~2~loc_i$ ，即访问版本 $v_i$ 中的 $a_{{loc}_i}$ 的值，注意：生成一样版本的对象应为 $v_i$ 。

输出格式：
输出包含若干行，依次为每个操作2的结果。
数据范围：
对于 100% 的数据： $1 \leq N, M \leq {10}^6, 1 \leq {loc}_i \leq N, 0 \leq v_i < i, -{10}^9 \leq a_i, {value}_i \leq {10}^9$

就是上边的模板，拿来用即可。

1
#include <bits/stdc++.h>
2
#define N 1000010
3
using namespace std;
4

5
struct HJTTree {
6
    int l, r;
7
    int dat;
8
} tree[N << 5];
9
int idx = 0, root[N];
10
int a[N];
11

12
int build(int l, int r) {
13
    int p = ++idx;
14
    if (l == r) {
15
        tree[p].dat = a[l];
16
        return p;
17
    }
18
    int mid = (l + r) >> 1;
19
    tree[p].l = build(l, mid);
20
    tree[p].r = build(mid + 1, r);
21
    return p;
22
}
23

24
int clone(int u) {
25
    int p = ++idx;
26
    tree[p] = tree[u];
27
    return p;
28
}
29

30
int insert(int u, int pos, int dat, int l, int r) {
31
    int p = clone(u);
32
    if (l == r) {
33
        tree[p].dat = dat;
34
        return p;
35
    }
36
    int mid = (l + r) >> 1;
37
    if (pos <= mid) tree[p].l = insert(tree[u].l, pos, dat, l, mid);
38
    else tree[p].r = insert(tree[u].r, pos, dat, mid + 1, r);
39
    return p;
40
}
41

42
int query(int idx, int pos, int l, int r) {
43
    if (l == r) return tree[idx].dat;
44
    int mid = (l + r) >> 1;
45
    if (pos <= mid) return query(tree[idx].l, pos, l, mid);
46
    return query(tree[idx].r, pos, mid + 1, r);
47
}
48

49
int main() {
50
    ios::sync_with_stdio(false);
51
    cin.tie(nullptr);
52
    cout.tie(nullptr);
53

54
    int n, m;
55
    cin >> n >> m;
56
    for (int i = 1; i <= n; i++) cin >> a[i];
57
    int tot = 0;
58
    root[0] = build(1, n);
59
    while (m--) {
60
        int ver, pos, op;
61
        cin >> ver >> op >> pos;
62
        if (op == 1) {
63
            int dat;
64
            cin >> dat;
65
            root[++tot] = insert(root[ver], pos, dat, 1, n);
66
        } else {
67
            cout << query(root[ver], pos, 1, n) << endl;
68
            root[++tot] = root[ver];
69
        }
70
    }
71
    return 0;
72
}

洛谷 P3834 [模板] 可持久化线段树 2#

题目地址：P3834

题目难度：提高+/省选-

给定 $n$ 个整数构成的序列 $a$ ，将对于指定的闭区间 $[l, r]$ 查询其区间内的第 $k$ 小值。
输入格式：
第一行包含两个整数，分别表示序列的长度 $n$ 和查询的个数 $m$ 。第二行包含 $n$ 个整数，第 $i$ 个整数表示序列的第 $i$ 个元素 $a_i$ 。接下来 $m$ 行每行包含三个整数 $l, r, k$ , 表示查询区间 $[l, r]$ 内的第 $k$ 小值。
输出格式：
对于每次询问，输出一行一个整数表示答案。
数据范围：
对于 ${100\%}$ 的数据，满足 ${1 \leq n,m \leq 2\times 10^5}$ ， ${0\le a_i \leq 10^9}$ ， ${1 \leq l \leq r \leq n}$ ， ${1 \leq k \leq r - l + 1}$ 。

~~这才是可持久化线段树的标准应用~~。这道题有很多种做法，最经典的是可持久化线段树，此外还有归并树、划分树、树套树（线段树套平衡树）。

此时维护另外一个变量 $s_{i,j}$ ，代表值落在 $[i,j]$ 之间的数的个数。在递归过程中，查看 $s_{l,mid}$ 和 $s_{mid+1,r}$ 与 $k$ 的大小关系。如果 $s_{l,mid}\geq k$ ，证明待查询数字在左区间内，递归到左区间；否则该数字在右区间，递归到右区间查找第 $k-s_{l,mid}$ 大数即可。这类似于二叉搜索树的排名查询操作。

如果只考虑右区间，即查询 $[1,r]$ 内的第 $k$ 大数，我们可以限定主席树的起始查找下标实现查询。但是我们加入了左区间，变成了 $[l,r]$ ，就不好搞了。但是当我们按照链式插入（为每个点单独分配一个根节点和副本树）数据时，它满足一个可减性，这意味着我们可以用类似前缀和的方式来处理任意区间。那么此时的 $s_{l,mid}$ 就可以用 $R$ 子树记录的 $s_{l,mid}$ 减去 $L-1$ 子树的 $s_{l,mid}$ 得到。

1
#include <bits/stdc++.h>
2
#define N 200010
3
using namespace std;
4

5
struct HJTTree {
6
#define leftSubtree(idx) (tree[tree[idx].l])
7
#define rightSubtree(idx) (tree[tree[idx].r])
8
    int l, r;
9
    int cnt;
10
} tree[N << 5];
11
int idx = 0, root[N];
12
int a[N];
13
vector<int> num;
14

15
int find(int x) {
16
    return lower_bound(num.begin(), num.end(), x) - num.begin();
17
}
18

19
void pushup(int idx) {
20
    tree[idx].cnt = (leftSubtree(idx).cnt + rightSubtree(idx).cnt);
21
}
22

23
int build(int l, int r) {
24
    int p = ++idx;
25
    if (l == r) return p;
26
    int mid = (l + r) >> 1;
27
    tree[p].l = build(l, mid);
28
    tree[p].r = build(mid + 1, r);
29
    return p;
30
}
31

32
int clone(int u) {
33
    int p = ++idx;
34
    tree[p] = tree[u];
35
    return p;
36
}
37

38
int insert(int u, int pos, int l, int r) {
39
    int p = clone(u);
40
    if (l == r) {
41
        tree[p].cnt++;
42
        return p;
43
    }
44
    int mid = (l + r) >> 1;
45
    if (pos <= mid) tree[p].l = insert(tree[u].l, pos, l, mid);
46
    else tree[p].r = insert(tree[u].r, pos, mid + 1, r);
47
    pushup(p);
48
    return p;
49
}
50

51
int query(int l, int r, int L, int R, int k) {
52
    if (l == r) return l;
53
    int mid = (l + r) >> 1;
54
    int left = leftSubtree(R).cnt - leftSubtree(L).cnt;
55
    if (left >= k) return query(l, mid, tree[L].l, tree[R].l, k);
56
    return query(mid + 1, r, tree[L].r, tree[R].r, k - left);
57
}
58

59
int main() {
60
    ios::sync_with_stdio(false);
61
    cin.tie(nullptr);
62
    cout.tie(nullptr);
63

64
    int n, m;
65
    cin >> n >> m;
66
    for (int i = 1; i <= n; i++) {
67
        int x;
68
        cin >> x;
69
        a[i] = x;
70
        num.push_back(x);
71
    }
72
    sort(num.begin(), num.end());
73
    num.erase(unique(num.begin(), num.end()), num.end());
74
    root[0] = build(0, num.size() - 1);
75
    for (int i = 1; i <= n; i++) root[i] = insert(root[i - 1], find(a[i]), 0, num.size() - 1);
76
    while (m--) {
77
        int l, r, k;
78
        cin >> l >> r >> k;
79
        cout << num[query(0, num.size() - 1, root[l - 1], root[r], k)] << endl;
80
    }
81
    return 0;
82
}

音乐

JustPureH₂O

穷方圆平直之情，尽规矩准绳之用

音乐

[熟肉] 一棵主席树新增了一个数据，这是它的结构发生的变化

可持久化简介#

可持久化线段树/主席树理论基础#

可持久化线段树/主席树建树部分#

可持久化线段树/主席树节点插入#

模板两题#

洛谷 P3919 [模板] 可持久化线段树 1（可持久化数组）#

洛谷 P3834 [模板] 可持久化线段树 2#

支持与分享

评论区

音乐

目录

音乐

JustPureH2O

穷方圆平直之情，尽规矩准绳之用

音乐

[熟肉] 一棵主席树新增了一个数据，这是它的结构发生的变化

可持久化简介#

可持久化线段树/主席树 理论基础#

可持久化线段树/主席树 建树部分#

可持久化线段树/主席树 节点插入#

模板两题#

洛谷 P3919 [模板] 可持久化线段树 1（可持久化数组）#

洛谷 P3834 [模板] 可持久化线段树 2#

支持与分享

评论区

音乐

目录

JustPureH₂O

可持久化线段树/主席树理论基础#

可持久化线段树/主席树建树部分#

可持久化线段树/主席树节点插入#