移动端 Banners
881 字
4 分钟
CF 755D - PolandBall and Polygon 题解

Done
您已获得最佳的阅读体验!
题目地址:CF 755D
题目难度:提高+/省选-
给出一个
边形,和距离 。 第一次连接 和 ,第二次连接 和 ,依次进行 次,每次结束后输出 边形被分割成了几个区域。
,保证 和 互质。
今天模拟赛 T2 原题,赛时多测卡线段树加上多测没清空喜爆零。同机房大佬 Brilliant11001 用
为了取模方便,本文是 0-index 的。
首先,根据互质关系可得,本题无需考虑重边的情况。因为在 0-index 下,题目可以看作是
手搓可以发现第一个规律:
接着研究,发现第二个规律——连边带来的贡献是当前边与已有边的相交次数加一。我们的核心任务就是维护当前边会与多少已连接的边相交。
假设当前待连的边是
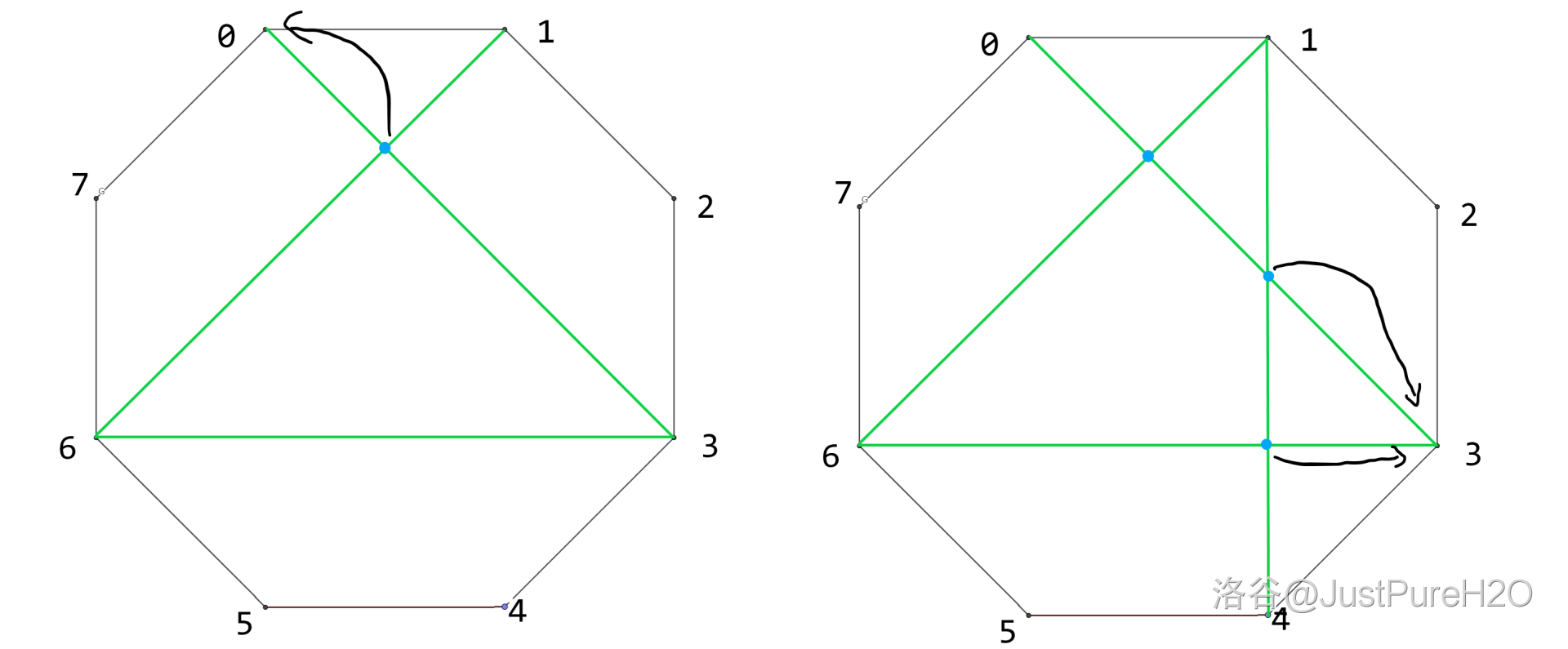
线段树的常数还是很大的,建议使用树状数组(或者上边大佬的数学做法)。
#include <bits/stdc++.h>#define N 1000010using namespace std;
typedef long long ll;
struct SegmentTree {#define le(x) (x << 1)#define ri(x) (x << 1 | 1)#define leftSubtree(x) (tree[le(x)])#define rightSubtree(x) (tree[ri(x)]) int l, r, size; ll sum;} tree[N << 2];
void pushup(int idx) { tree[idx].sum = leftSubtree(idx).sum + rightSubtree(idx).sum;}
void build(int idx, int l, int r) { tree[idx].l = l, tree[idx].r = r; tree[idx].size = r - l + 1; if (l == r) return; int mid = (l + r) >> 1; build(le(idx), l, mid); build(ri(idx), mid + 1, r); pushup(idx);}
void modify(int idx, int uid) { if (tree[idx].size == 1 && tree[idx].l == uid) { tree[idx].sum++; return; } int mid = (tree[idx].l + tree[idx].r) >> 1; if (uid <= mid) modify(le(idx), uid); if (uid > mid) modify(ri(idx), uid); pushup(idx);}
ll query(int idx, int l, int r) { if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].sum; int mid = (tree[idx].l + tree[idx].r) >> 1; ll ret = 0; if (l <= mid) ret += query(le(idx), l, r); if (r > mid) ret += query(ri(idx), l, r); return ret;}
int main() { ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
int n, k; cin >> n >> k; k = min(k, n - k); build(1, 0, n - 1); int pos = 0; ll section = 1; for (int i = 1; i <= n; i++) { int L = (pos + 1) % n, R = (pos + k - 1 + n) % n; // 左右端点 ll sum = R < L ? query(1, 0, R) + query(1, L, n - 1) : query(1, L, R); // 获得区间内每个点连出去多少条边,注意判断是否跨过节点 0 modify(1, pos); // 为当前的线段端点累加 1 modify(1, (pos + k) % n); section += sum + 1; // 图形总数 pos = (pos + k) % n; // 跳到下一个位置 cout << section << ' '; }
return 0;}支持与分享
如果这篇文章对你有帮助,欢迎分享给更多人或赞助支持!
CF 755D - PolandBall and Polygon 题解
https://justpureh2o.cn/articles/755/ 最后更新于 2024-11-27,距今已过 458 天
部分内容可能已过时

































































































