线性代数 简明教程

前言
本文是
需要注意的是:本教程中的矩阵表示方法可能与你在课上或是其他教程中看到的有些许出入。为了兼具美观和统一,单行行向量用圆括号包围,变量顶部用向量符号标记,如行向量:
第一章 矩阵与方程组
相信大多数人入门线性代数的第一堂课就是学习如何利用矩阵求解线性方程组的吧。矩阵作为一个仅由数字和括号组成的表示方法,既避免了书写各种未知数符号的麻烦,也能一眼看出各未知量之间的数量关系,实属上乘的表示方法。矩阵的一些特殊性质也可以帮助我们解决一些难以解决的问题。
第一节 方程组与矩阵的互相转化
假设我们有一个方程组:
如此得到的矩阵叫做系数矩阵,顾名思义,它只表示了原方程组的系数,而忽略了常数项。
它同时也是一个
一般地,对于一个
矩阵( ),它有 行 列。
此时,如果我们加上等号右侧的常数项,原先的
人们为了区分常数和系数,选择在书写时将常数加入到最右侧那一列,并且在最右一列的前面加上竖线分隔系数,如此得到的矩阵叫做增广矩阵。
本例中
当矩阵元素不明时,我们为了简便表示矩阵本身,采用字母 + 下标 + 括号的方式。例如一个
矩阵 ,可以写作: 。
第二节 矩阵的基本运算
一. 矩阵加法
构造相同的矩阵,即两个矩阵行列数相同,称这样的两个矩阵是同型的。
矩阵加法仅限两个同型矩阵,相加时同一行同一列的元素相加即可(增广矩阵同理)。
例如:
矩阵加法满足:结合律、交换律
二. 矩阵减法
矩阵减法是矩阵加法的逆运算,因此对于两个矩阵的形式要求同上,只是相同位置的元素相减而已。
矩阵减法满足:结合律、交换律
三. 标量乘法/矩阵数乘
矩阵的数乘也很简单,让矩阵中每个元素乘以这个数就可以了。
例如:
矩阵数乘满足:交换律、结合律、分配律
四. 矩阵转置
将原矩阵的行变成新矩阵的列,称为矩阵的转置。
直观理解就是顺时针旋转 90 度后再水平镜像过去。转置用上标
例如:
矩阵的主对角线(左上 - 右下)元素转置前后不变,且具有可逆性 [
转置后恰好就是它自身的矩阵称为对称矩阵。它是自转置的,即
。对称矩阵的元素恰好关于主对角线对称,且是一个 的方阵。
五. 矩阵乘法
该内容将在第二章涉及。
第三节 消元
按照一般思路(就是我们在小学学的方法),我们会选择通过方程互相加减各自的倍数,达到消去未知数的目的。这种方法在矩阵上同样适用,而且它有一个贼高坤的名称:高斯消元法(Gaussian Elimination)。
回忆一下我们从出生就会用的消元原理,我们的目标就是让每个未知数都对应一个常数项,那么它的值就可以直接用常数除以系数的方式求出。矩阵中也是如此,为了能够化简出可直接求解的矩阵,我们在此引入初等行变换的概念:
- 交换某两行
- 把矩阵的某一行同乘以一个非零的数
- 把某行的若干倍加和到另一行
这三条很容易理解。第一条:相当于交换方程组顺序,不影响计算;第二条:相当于对某一行方程放缩某倍,它等价于原方程;第三条:相当于前两条的融合,也是消元的关键一招。这三条规则在之后的初等矩阵内容中会再次出现。
首先从一个例子讲起,让读者感受一下初等行变换的魅力:
考虑这个方程组:
按照如上所述,将它转写成增广矩阵的形式:
我们总结一下常用的消元原理,应用到矩阵上就是:
- 枚举每一列
- 通过加减有序组中某一行的非零倍,将之后所有行的第
令矩阵
枚举第一列,
第二步,自乘并标记有序,因此第一行除以
第三步,将无序组的第
枚举第二列,此时
最终的最终,第三行减
为什么把矩阵化简成这种金字塔型的形式呢?你会发现:最后一行仅有一个带系数的未知数
一般地,对于一个矩阵,如果它的非零系数呈阶梯形分布,则称这类矩阵为行阶梯形矩阵。将非零系数挑出来,它们组成的是一个上三角形矩阵;对应地,零项就会组成下三角矩阵。上三角矩阵通常以
原方程组有唯一解:
在这里,我没有给出代码实现。因为对于一些特殊情况,化简出的矩阵不能很好地被计算机处理,更适合算法竞赛体质的高斯消元模板将在本章第五节给出。
第四节 秩
类比一元二次方程的实数根存在性判别法 ——
答案是有的,而且不止一种,这意味着“矩阵是否有解” 这样的问题会有多种解决方案。现在介绍的是最为简单常用的一种——秩。
在线性代数中,一个矩阵 A 的列秩是 A 的线性独立的纵列的极大数目。类似地,行秩是 A 的线性无关的横行的极大数目。即如果把矩阵看成一个个行向量或者列向量,秩就是这些行向量或者列向量的秩,也就是极大无关组中所含向量的个数。
……咱们抛掉这种看也看不懂的高级语文句法,听我给你总结:
通俗来讲,把一个矩阵化成最简形式(特指行阶梯形)后,非零行的个数就是矩阵的秩。这其实是秩的最大线性无关组的定义。再次白话总结:如果存在三个行向量(列向量一样的,保证所有向量都是行 / 列向量即可):
矩阵
现在明白了吧,如果一个矩阵的某两行线性相关,它们都会被初等行变换第三条狠狠薄纱 —— 在乘或除以一个非零数后相减,其中一行就会被全部消成 0,从方程组角度来看就是
当然上边这一段也有表述不准确之处,假设有一个增广矩阵
第二行不乐意了,它还存留这最后一点倔强,好像在说:“你总结的不对呢真是雑鱼”。但是明眼人都看得出来,
再考虑有无穷解的情况:无非就是出现了
最后就是有唯一解:如果一切进行顺利的话,既没有全零行,也没有无解行。那么此时系数矩阵和增广矩阵的秩会相同,且等于未知数个数,即
总结,假设一个由
例 1.4.1 Delivery Mathematics 快递员的数学题
「稻妻狛荷屋的人气跨国快递员绮良良在送货途中遇到了一个难题,你作为无所不知无所不晓的旅行者自然是乐意地接下了她的委托。当你来到委托地点时,你发现这是一道解谜题目……」
稻妻号称最难的方块解谜是一组由
个正方体可旋转方块组成的阵列,击打其中的某个方块会使得与之相关联的其他方块共同旋转一个特定角度。在这个谜题中,每个方块每次仅能水平顺时针旋转 90 度,传动方式在下图给出。问若要使所有方块同时朝向北方,需要如何击打方块?给出任意可行解,但需要保证每个方块旋转的次数不超过 4(不击打也可以,相当于次数为 0)。 由于钟离先生远在海那一头的璃月喝茶听评书、宵宫也正忙着制作夏日祭的烟花而无法抽身、香菱在万民堂做饭、安柏在侦察蒙德郊区、芙宁娜忙着吃蛋糕…… 总之没有其他人
召唤物能帮你解决这个问题,你只能凭借自己的力量解开这个谜题。
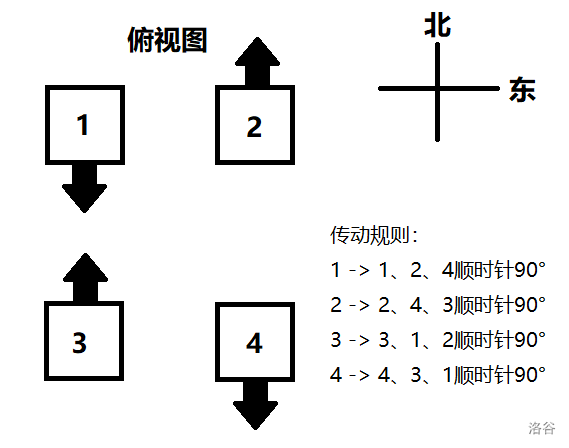
问题分析:首先我们要搞清楚传动规则,我们会发现当你击打了一个方块,包括它在内、再按顺时针方向数两个方块都在旋转相同的角度。这也是这道题被称作难题的原因之一,只用想象力是很难想象的出来的…… 于是为了用代数方法解决该问题,我们选择用四个未知数、四个方程表示每个方块操作后的状态,问题解决的标志既为四个方块的状态均为
算法设计:考虑到单个方块每旋转四次就相当于一次循环,因此我们重定义方向标,从北开始,顺时针方向将方位标记为
解:设方块 1-4 的击打次数分别为
根据传动规则,有如下线性方程组:
增广矩阵形式为:
(化简过程略),行阶梯形式为:
因为系数矩阵的秩与增广矩阵的秩相同且都等于未知数个数
因此,最佳方案是暴击击打 2 号和 3 号方块各两次。
后日谈:有些读者可能会问,这个难道不是有无穷解吗?为什么上边说这个矩阵只有唯一解?其实这个矩阵确实只有唯一解,因为
对于有
第五节 计算机高斯消元
一. 实数高斯消元
基本思路与手推时相同:
- 找到当前列元素绝对值最大的那一行,并移动到无序组的上端。
- 将这一行的第一个元素除成
此时需要进行一个神秘步骤:让除开当前行和第
如果有唯一解,我们会得到一个主对角线全为
- 枚举每一行,找到当前行第一个非零元素,并记录它的结果为右侧常数。该行的其余元素作为自由元,不作操作(或赋值为任意值)
- 重复操作直到遍历到全零行。
我们会发现上三角矩阵中同一列可能有多个非零系数,这意味着上层方程组的结果依赖于下层的求解,如果出现自由元将会十分棘手。用上述方法将矩阵进一步化为对角矩阵后,就不会存在这种依赖关系了,因而判断和输出变得简单了许多。
核心代码如下:
int gauss() { int rank = 0; // 秩 for (int c = 1, r = 1; c <= n; c++) { int t = r; for (int i = r; i <= n; i++) { if (abs(matrix[i][c]) > abs(matrix[t][c])) t = i; // 找出主元绝对值最大的那一行 } if (abs(matrix[t][c]) < EPS) continue; // 非零才能消成1 if (t != r) swap(matrix[t], matrix[r]); // 交换 for (int i = n + 1; i >= c; i--) matrix[r][i] /= matrix[r][c]; // 主元消成1 for (int i = 1; i <= n; i++) { // 反复消元,成为对角线矩阵 if (abs(matrix[i][c]) > EPS && i ^ r) { // 当前行不消,若当前位已经是零了也不消 for (int j = n + 1; j >= c; j--) { matrix[i][j] -= matrix[i][c] * matrix[r][j]; // 消成零 } } } r++; rank++; } if (rank < n) { // 无解or无数组解 for (int i = rank + 1; i <= n; i++) { for (int j = 1; j <= n + 1; j++) { if (abs(matrix[i][j]) > EPS) return NO_SOLUTION; // 无解 } } for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { if (abs(matrix[i][j]) > EPS) { ans[j] = matrix[i][n + 1]; // 无数组解,找到主元并直接赋值,剩余的自由元自动赋值为0 break; } } } return INFINITE_SOLUTIONS; } for (int i = 1; i <= n; i++) ans[i] = matrix[i][n + 1]; // 有唯一解,此时常数项即为答案 return UNIQUE_SOLUTION;}复杂度
二. 同余高斯消元
上一节的例题就是同余高斯消元的一个典例,我们需要求解模
复杂度
三. 异或高斯消元
适用于方程组和奇偶性相关联的时候,此时列出的方程组是异或和起来的。鉴于方程组的系数只有 bitset 来优化时间复杂度。
int gauss() { int rank = 0; // 矩阵的秩 for (int c = 1, r = 1; c <= n; c++) { int t = r; for (int i = r; i <= n; i++) { if (matrix[i].test(c)) { // 找到绝对值最大的行(只要第一个系数是 1 即可) t = i; break; } } if (!matrix[t].test(c)) continue; // 跳过零行 if (t ^ r) swap(matrix[r], matrix[t]); // 交换到第一行
for (int i = 1; i <= n; i++) { // 与普通高斯消元的不同之处,对 1~n 行全部消元 if (matrix[i].test(c) && i ^ r) { // 当前行不消,零行不消 matrix[i] ^= matrix[r]; // 异或代替减法进行消元 } } r++; rank++; } if (rank < n) { // 秩小于 n,可能是无数组解、有可能无解 for (int i = rank + 1; i <= n; i++) { if (matrix[i].test(n + 1)) return NO_SOLUTION; // 存在类似于 0=k 的矛盾情况,无解 } for (int i = 1; i <= n; i++) { for (int j = 1; j <= n + 1; j++) { if (matrix[i].test(j)) { // 无数组解,找到主元并赋值 ans[j] = matrix[i][n + 1]; break; } } } return INFINITE_SOLUTIONS; } for (int i = 1; i <= n; i++) ans[i] = matrix[i][n + 1]; // 有唯一解,对角矩阵每个未知数的解就是常数项的值 return UNIQUE_SOLUTION;}复杂度
洛谷习题:
- P3389 [模板] 高斯消元法
- P2455 [SDOI2006] 线性方程组
- P4035 [JSOI2008] 球形空间产生器
- P10315 [SHUPC2024] 原神,启动!
- P6126 [JSOI2012] 始祖鸟
- P2447 [SDOI2010] 外星千足虫
第二章 矩阵乘法
第一节 什么是矩阵乘法
你经常能在各种线性代数的书上看到这样一串定义式:比如说我自己)其实是非常不友好的。他们在举例计算时很容易被
将左边的矩阵的每一行看作每个未知数都代了确定值的方程、右边的矩阵每一列看作是前者方程的未知数系数。二者相乘本质上就是让未知数和系数匹配上,并计算出结果放入结果矩阵的特定位置。这个特定位置也有讲究,假如选择了前一个矩阵的

那么什么样的矩阵才能进行乘法运算呢?答案是一个 矩阵乘法国不养闲人,这种单身汉显然是不可以光天化日下大摇大摆出来遛弯的。因此保证其中一个矩阵的行数等于另一个矩阵的列数后方可相乘。
类比四则运算的乘法,矩阵乘法是否也有结合律、分配律和交换律呢?很遗憾,不完全是,前二者是矩阵乘法运算所具备的性质、但最后那个交换律不是。不是所有的矩阵相乘都满足乘法交换律。但是还是有满足交换律的特例:同型零矩阵相乘、一个矩阵(可逆)和它的逆矩阵相乘,矩阵乘法满足交换律的充要条件证明过于复杂烧脑,此处不做陈述主要是我也不会证满足交换律的充要条件 qwq……。
证明:一般矩阵不满足乘法交换律
假设一般矩阵
假设
矩阵和数字一样,也有幂次方的计算。特殊地,任意
例 2.1.1 Akasha Browser with Irminsul Kernel 世界树搜索引擎
你作为刚刚清除了须弥世界树痼疾的英雄旅行者,突然对虚空终端的运作方式有了兴趣。你从大贤者那里了解
逼问到,虚空终端实质上是一个仅显示搜索结果的前端程序,但关键词搜索功能却是基于须弥地下空间的世界树。带着这个疑问,你再次来到了世界树前,见到了小吉祥草王大人,希望能让她告诉你世界树的运作方式……
背景知识: 很多浏览器的检索功能都依赖于矩阵运算,这里属于最简单的一种——我们只需要矩阵的乘法运算(某些情况下会用到转置,甚至正交性)。然而随着科技的快步发展,数据量的快速增加,这种方式如今只在很小的范围内被使用(由于码量小思维简单,它有时会在个人博客的关键词搜索功能中被用到);目前广泛使用的一种是向量相似性搜索,它本质上是在一定范围内搜索与目标向量辐角最为接近的已有向量,在“矩阵的几何表示” 章节中会涉及到。这里介绍的是简单匹配搜索。
问题分析:因为矩阵乘法本质上是未知数和系数的配对求值,我们需要构造一个方法来使得“搜索内容” 和“已有内容” 配对。并且搜索引擎总会返回与你搜索的内容最为相似的结果,搜索“比尔・盖茨”,第一条肯定是关于他个人的介绍,而绝对不可能是一则寻狗启示……因此,我们设计的矩阵必须能在经历一轮运算后能够正确返回每个关键词出现的频率(简单点说就是出现次数),这样虚空终端才能对频率进行排序,并返回频率最大的那个结果。
算法设计:不妨考虑这样几个矩阵 —— 其中一个存储关键词、另一个存储搜索内容。比如我需要将几篇论文(为方便使用英文表示,并且假设词根相同的单词为同一个单词,即不考虑词汇变形)《Basic Structure of Elemental Monuments》(元素方碑的底层构造)、《Junior Elemental Reaction》(初等元素反应)、《Advanced Elemental Theory》(高等元素论)、《Architectural Structure in the Mausoleum of King Deshret》(赤王陵的建筑结构)以及《Advanced Sumeru Linguistic Analysis》(高等须弥语音学解析)。我们在此次挑选一些关键词存储(方便读者观察):Structure、Element、Junior 和 Advanced。为每篇论文编号 1-5,矩阵如下图:

假如热爱学习的艾尔海森来到了教令院的大图书馆,它想测试一下这全新开发的文献查询系统,输入了 Advanced 一词。假设已录入数据库就是以上形式,我们如何构造一个“查询矩阵” 来和数据库矩阵进行运算呢?
首先根据矩阵乘法的前提要求,这个查询矩阵必须是四行。不妨让每行代表我们的词库词语,艾尔海森输入的是 Advanced—— 即对应数据库矩阵的第四列(未知数),我们要配对它的系数,因此它必须在第四行,才能保证系数正确匹配未知数。同理,查询矩阵的第一行对应 Structure、第二行 Element、第三行 Junior。他输入了一个 Advanced,因此我们的查询矩阵如下图:
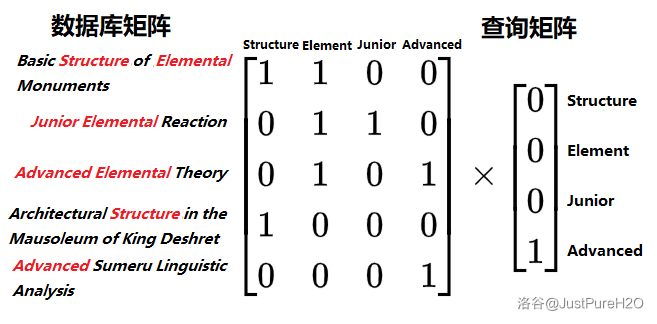
乘法的目的是将二者匹配起来,得到的结果如下图:
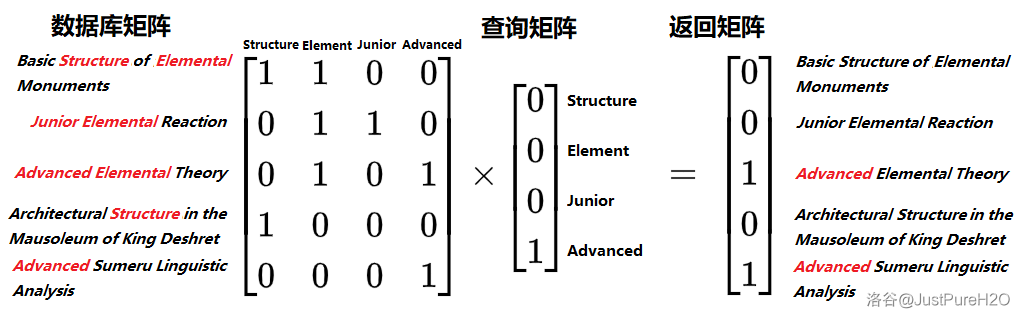
返回矩阵的数字代表关键词在对应数据库项中的出现次数,也就是说,如果此时再加入一篇论文《Advanced Usage of the Word Advanced》(“Advanced” 一词的进阶用法),返回矩阵的最后一行(第六行)会出现一个
例 2.1.2 Light Novel Query 轻小说查询
八重堂的主编八重神子最近在为轻小说的事情发愁…… 并不是因为销量不够,正相反:八重堂最近推出了一项跨国销售项目,各种经典作品被远销往了枫丹廷。这就牵涉出一个问题 —— 枫丹的市民们不想远离枫丹城区、横穿须弥沙漠、翻越璃月高山、躲避稻妻雷暴就为了看一看有哪些轻小说符合自己的独特口味…… 于是八重神子找到了见多识广的你,希望你能帮她做出一套轻小说内容检索系统。当然作为报酬给你的原石和摩拉是肯定是不会少的……
当然,这套系统有一定要求。因为有很多轻小说为了吸引读者,取的标题和内容是完全对不上号的,神子的想法是做一套正文内容检索 —— 每本轻小说的总字数在出版时就统计好了,但是苦于稻妻的信息存储技术不是很发达,神子希望存储在数据库矩阵里的数据尽可能小。请问该如何设计符合要求的存储算法?
问题分析:每本书中特定的词可能重复出现成百上千次(同样用英文单词表示,且同词根不同词形的两个词算作同一个单词参与计数),我们的要求是让数据尽可能小,既然总字数都已经给出了,我们不妨使用指定词出现的频率来表示这个词的出现次数(单词出现次数 = 全书总词数 × 出现频率)。这样的搜索方法叫做相对频率搜索。
算法设计:大致原理和例 2.1.1 里的一模一样,只是数据库矩阵存储的不再是出现总次数,而是对应词的相对频率。因而图例 2.1.3 可以变化为如下形式:

明显一看,第三篇文章出现 Advanced 的频率最高,应该优先返回。但是这个例子并不是很好(明明说了按内容搜索你还在这搜索标题),但是当加入大量的正文内容时,这个方法的优势也就体现出来了。这里由于篇幅原因就不举过于复杂的例子,本例仅作对相对频率搜索的原理的理解。
第二节 初等矩阵与矩阵递推
假设存在一个
仅交换了两行的单位矩阵称作第 I 类初等矩阵(只进行了初等行变换第一条),将它左乘到一个矩阵前,可以进行相应的行运算;右乘到一个矩阵后可以进行相应的列运算。比如,一个第 I 类初等矩阵
仅将某一行乘以一个非零倍数的矩阵叫做第 II 类初等矩阵(只进行了初等行变换第二条),左乘行运算、右乘列运算。例如一个第 II 类初等矩阵
仅将某一行的非零倍加到另一行上的矩阵叫做第 III 类初等矩阵(只进行了初等行变换第三条),同样是左乘行运算、右乘列运算,但是有一点点小不同,不要根据思维定势随便写答案!例如一个第 III 类初等矩阵
因此我们可以不必使用高斯消元,仅使用初等矩阵乘法也可以达到将普通矩阵消元变成最简行阶梯形矩阵!而且它可以进行列运算,甚至比高斯消元法更高级一点。
接下来是我们的矩阵递推。大家都知道斐波那契数列,它的前两项均为 1,此后的每一项都是前两项之和,即
#include <bits/stdc++.h>using namespace std;
long long fib(int n){ if (n == 1 || n == 2) return 1; return fib(n - 1) + fib(n - 2);}
int main(){ int n; cin >> n; cout << fib(n) << endl; return 0;}这段代码其实就是照搬了上面的通项公式,但是递归有个弊端就是效率和内存,当
首先我们将通项公式变成我们想要求的形式,为了便于输出,要求结果矩阵的第一个元素就是答案,因此结果矩阵就是:
那么求数列第
#include <bits/stdc++.h>#define MOD 1000000007#define N 15using namespace std;
typedef long long ll;
int n = 2; // 递推矩阵行列数均为2
struct Matrix { ll mat[N][N];
Matrix() { memset(mat, 0.0, sizeof mat); // 初始化时内部变量自动置零,无需每次定义变量时再置零 }
void I() { for (int i = 1; i <= n; i++) mat[i][i] = 1; // 构造2×2单位矩阵 }};
Matrix operator*(const Matrix& l, const Matrix& r){ // 重载乘法运算符,实现矩阵乘法 Matrix res; for (int k = 1; k <= n; k++) { for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { // res.mat[i][j] = (res.mat[i][j] + l.mat[i][k] * r.mat[k][j] % MOD) % MOD; // 取模用这个 res.mat[i][j] += l.mat[i][k] * r.mat[k][j]; } } } return res;}
Matrix qpow(Matrix a, ll b){ Matrix res; res.I(); // 单位矩阵相当于实数运算中的 1,因此任何矩阵乘以一个单位矩阵的结果都是这个矩阵 while (b) { if (b & 1) res = res * a; a = a * a; b >>= 1; } return res;}
int main(){ int a; cin >> a;
Matrix A; A.mat[1][1] = A.mat[1][2] = 1; // 初始矩阵 Matrix M; M.mat[1][2] = M.mat[2][2] = M.mat[2][1] = 1; // 递推矩阵 A = A * qpow(M, a - 1); cout << A.mat[1][1] << endl; return 0;}它的时间复杂度可以做到
例 2.2.1 Lost Control! Blubberbeast’s Reproduction 膨膨兽泛滥危机
由于枫丹水质的大幅改善,膨膨兽的天敌数量锐减,枫丹城区近海的膨膨兽也得到了更多的食物,进而开始大量地繁殖。水质改善的第一年,已登记的膨膨兽数量是
头,恰好是斐波那契数列的第 项。第二年,膨膨兽数量没有变化,之后的每一年,膨膨兽数量都是前两年之和的 ,已知膨膨兽的平均寿命是 15 年、枫丹廷近海能承载的最大膨膨兽数量是 万只。那么请问 年后近海的膨膨兽数量是多少?这 年内枫丹廷是否需要向近海投放膨膨兽的天敌以遏制后者疯狂繁殖?(结果出现出现小数则向上取整)
问题分析:这是一道标准的矩阵快速幂递推问题,它基于斐波那契数列递推、却比它更高级。首先,它的初始值不再是
算法设计: 已知初始矩阵
对于前项和的问题,前面已经给出了,因而我们的递推矩阵变成了
代码实现上,仅需将
最终结果:875076。结果小于 90 万,因此不需要投放天敌。
后日谈:那如果将系数改变为 977427,接近 100 万了。可见其增长速度之恐怖。
洛谷例题:
第三章 矩阵的逆
第一节 浅谈矩阵的逆
“逆” 这个词相信你早已听说过:同余意义下存在乘法逆元,大多数矩阵也存在逆矩阵。“逆” 普遍用来描述不同意义下的“倒数” 的概念,倒数一般满足
如果对于一个矩阵
,存在另一个矩阵 ,使得: 成立。则称矩阵 是可逆的,或称之为非奇异的,矩阵 是矩阵 的逆矩阵,通常表示成 。特殊地,单位矩阵 的逆矩阵是它本身,即 ;零矩阵 不可逆,或称之为奇异的,即不可能存在矩阵 ,使得 。
这一点类比实数运算:
第二节 行列式
行列式是一种函数,写出来有点像矩阵的绝对值。它可以用来判断一个矩阵是否有解、也可以定量分析线性变换对原向量的影响。矩阵
定义
矩阵 的行列式为 。特殊地, 矩阵的行列式就是 的值。当一个矩阵的行列式为 时,它是奇异的、也就是不可逆的;反之则非奇异/可逆。
那我们在上边只提到了两种尺寸的方阵,那对于
第三节 代数余子式展开/
我们拿出祖传的
像上边这样,将
阶行列式中元素 ( )所在的第 行、第 列所有元素删去,剩下元素组成的新 阶行列式叫做原行列式的余子式,用 表示。
我们要计算整个
当
时,一个 的方阵的行列式可以表示成任意行/列的余子式展开,即: 这样的计算方式称作代数余子式展开,或
展开。
日常做题时,通常选取
第四节 矩阵的逆
第一节解释清楚了逆矩阵的概念,那么如何求逆矩阵呢?首先是前提——判断矩阵是否可逆!我们引入矩阵行等价的概念:
如果一个矩阵
能经过有限次初等行变换得到另一个矩阵 ,则称 与 是行等价的。
比如说你交换一个矩阵的两行(初等行变换第一条)得到的矩阵本质上还是原来的矩阵,因为如果当你把变换前后的矩阵拆分成一个个行向量,它们在坐标系上的关系不变(交换两行向量不变,同乘非零向量共线)。联系到第二节的初等矩阵知识,初等行变换可以转化为矩阵左乘初等矩阵,定义可以转换为如下的数学语言:
如果存在矩阵
和矩阵 ,使得 成立,则称 与 是行等价的;相应的,初等矩阵右乘就对应两个矩阵列等价。
矩阵行等价有反身性、传递性。例如:
相应的,若有方程组,使得
当且仅当
与 是等价方程组时,增广矩阵 与 行等价。
这个推论的证明需要用到一个定理:
若
为一个初等矩阵,则它是非奇异的,且 和 是同类型矩阵。
证明:根据初等矩阵的定义,它是由单位矩阵
第一种,
第二种,
第三种,
两个非奇异矩阵等价的条件是:假设
在矩阵运算中,(因为实在是太显而易见了所以很平凡)
证明:首先证第一条可以导出第二条。假设
再证第二条可以导出第三条。
最后证第三条可以导出第一条。根据行等价的定义,必有
根据第三条,我们就可以知道一个求逆矩阵的方法了:既然
例 3.4.1 How Aranaras Measure Timeflow 兰那罗的时间观念
你在须弥冒险时,遇到了森林可爱的孩子们 —— 兰那罗。这些小小的生物有着与世无争的纯净心灵、以及大大的胸怀。你们一同冒险,击败了桓那兰那故土的污秽化身,拯救了须弥森林。然而,在和兰那罗对话期间,除开他们奇妙的比喻之外,还有一件事情是你久久无法忘怀的 —— 他们的时间单位。你听过最多的是“种子长成大树”、“太阳升起又落下”、“落落梅从出生到长大”、“大树长成雨林”……
假如你们经过很长一段时间的交谈,你渐渐明确了各种时间描述词之间的数学关系,关系如下文所述。请你求出每个描述词所对应的时间间隔。
- 已知大树长成雨林的时间是种子长成大树的
倍。 - 树木从种子长成大树的期间,落落莓已经生长过整整
次了(由种子出生到果实成熟和从成熟到下一颗种子扎根生长的时间相同)。 - 兰那罗从种子长成大树期间,普通人已从黑发少年变为白发苍苍的老人了。
- 普通人从青年到老年的时间足够让三颗种子先后成长为大树。
- 一片树木生长成为雨林,不仅足够让
个人先后从少年变为老年,而且还需要额外的 年时间完全长成一片健康的雨林。 请问“大树长成雨林”、“树木从种子长成大树”、“兰那罗从种子变成大树”、“落落莓从扎根到成熟” 以及“普通人从少年到老年” 所经过的时间各是多少年?(四舍五入到最近整数,单位:年)
问题分析:既然各个描述词对应时长的倍数关系都已给出,我们可以两两列出方程组求解。这里我们用到矩阵的逆来方便求出方程的解。
算法设计:首先将各个描述词用未知数表示出来,再用数学关系表示出题干中各个描述词的关系,如此得到的 5 个方程恰好能使矩阵有唯一解。因为一般的方程
解:设“大树长成雨林”、“树木从种子长成大树”、“兰那罗从种子变成大树”、“落落莓从扎根到成熟” 以及“普通人从少年到老年” 的时间分别为
整理得:
对应系数矩阵
两侧同时乘以
高斯消元后,将
根据方程
解得:
因此,“大树长成雨林” 的时间是
最后,森林会记住一切。
第五节 行列式的性质
感谢初等矩阵的加持,我们需要记背的知识点又多了不少呢……
我们在第三节说了,用余子式计算矩阵行列式时,需要按照同一列或者是同一行展开。为什么不能沿对角线或者是其他花里胡哨的顺序算余子式呢?下面有个引理告诉你原因:
设
为 的方阵, 表示 的代数余子式,则:
不难发现,
假如
假如
推广到
根据
因此对于
也就是说,交换矩阵两行,其行列式变号;对某一行乘以一个数
对于一个
的上三角形矩阵,其行列式 。
对角线矩阵也是同理,计算它们的行列式只需要将主对角线上的元素累乘起来。当矩阵对应的方程组无解或者是有无数组解时,其行列式就一定是
第六节 行列式在高中数学中的应用
这一节的内容是 2024 年 11 月份新加入的。是适合高中生体质的快速解题技巧。
一. 向量叉乘/平行四边形面积
例题详见:2024 年新高考一卷 T16。
高中立体几何学了向量数量积/点乘,定义如下:
其中
是两向量间的夹角。结果为标量(实数)。
类比点乘,我们定义叉乘为:
模长为
,方向与参与运算的所有向量垂直的向量。
意义同上。结果为矢量(新向量)。
观察到这个模长很像正弦定理中三角形面积公式
联想到本节标题,其实二维向量叉乘是可以用
不到万不得已,考试时千万别用这一招,如果一定要用,请一定记住写出下面的证明过程才能保证不扣分或者扣分少一点。
证明:
从
那么:
此时将坐标
得证。
做题时又会发现,围成三角形的是两个三维空间向量,难道要用
答案是否定的,事实上我们可以想办法把它补充成一个完整的
我们可以加入基底向量
那是否意味着答案就是
首先方法本身是正确的,只是最后不能直接求和加绝对值!这也是把基底向量设为
相当于叉积的结果是一个新向量
二. 平行六面体体积
例题详见:《步步高一轮复习 83 练 2024 人教 A 版》 P355 T6
类比平行四边形,空间平行六面体也是可以用这个方法的。证明过于繁杂,不放了。事实上你可以用这个巧办法进行伪算,然后反解出一系列数值写到卷子上……对于由同样的三个三维向量围成的三棱锥,它的体积就应该是同向量构成的平行六面体的

三个等体积的三棱锥恰好填充了平行六面体的一半体积,即三棱锥体积是平行六面体的六分之一。手算时就可以用到先前介绍的代数余子式法选择零最多的行/列进行运算。
化学竞赛有时也会用行列式来求解平行六面体晶胞体积。事实上,任何由
例 3.6.1 Obsidian Opalstar 黑曜石奶奶
正如其他的占卜师那样,大名鼎鼎的「黑曜石奶奶」茜特菈莉在占卜前会也摆出各种各样的黑曜石晶体。然而她不同于普通占卜师的一点是——她的黑曜石可能来自于其他维度!其维度的高低、黑曜石在所处维度空间中的体积大小都取决于要占卜的事件。现在,你想让她帮你占卜一下“我什么时候能掌握线性代数”这一问题。茜特菈莉当然不会让你这么简单就得到她的回答,除非你能马上计算出她所用黑曜石的体积……
已知茜特菈莉所用的黑曜石是一块由
个四维向量围成的几何体,这四个向量分别是 (单位:cm),你能从她嘴里得到问题的结果吗?
问题分析:对于人工计算,可以选用代数余子式展开;对于计算机,可以使用高斯消元求解行列式。
解:问题即求解矩阵
的行列式的绝对值
洛谷例题:
第四章 向量空间
第一节 欧几里得向量空间
简称欧氏空间,
如果仅把
事实不然,我们发现,无论这个向量的起点如何变化,它们的方向(辐角)、长度(模长)相同,它们可以经过平移变换成同一个向量。只要确定以上这两项的值,一个

(向量
根据勾股定理可以计算出向量的长度,这叫做向量的模长,
高中数学教材在虚数那一章还有一个选学知识(2023 版)——辐角。尽管它标成“选学”,其实我们早在三角函数的几何表示里就接触过辐角了:一个起点是原点的向量可以看作是它从
向量的数乘运算:辐角不变,模长相乘。
图示:

(
向量的加法,参见高中物理合力与分力的知识。矢量(既有方向又有大小的量)的加法遵循平行四边形法则
图示:
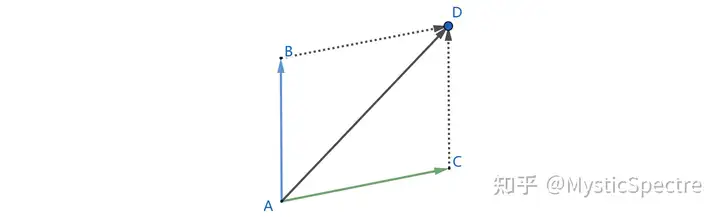
即以要进行加法的两个共起点向量为平行四边形的相邻边,做出完整的平行四边形,它们的和向量的起点与前两个向量起点相同,终点是平行四边形的对角顶点。上图中
和平行四边形法则等价的还有三角形法则:
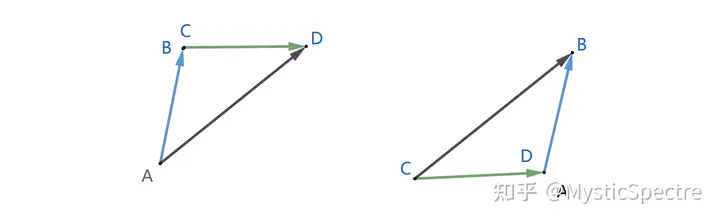
即将其中一个向量的起点平移到另一个向量的终点处,和向量的起点是后者的起点,终点是前者的终点。上图中
在向量表示中:
减法则是坐标相减,将减数向量做反向同模长的反向量再进行加法运算即可。
由于矩阵可以拆分成一个个列向量和行向量,而且矩阵的加法与数乘均与刚刚介绍的向量的加法与数乘规则相同。因此矩阵具备表示向量组的条件,称之为向量空间。向量空间中定义的加法和数乘需要满足如下几条(假设
Undefined control sequence \bold Undefined control sequence \bold Undefined control sequence \bold Undefined control sequence \bold Undefined control sequence \bold Undefined control sequence \bold Undefined control sequence \bold Undefined control sequence \bold
好多啊 ccc,其实就是需要把“加法” 定义成正统的加法(满足交换律、结合律);“数乘” 定义为正规的数乘(满足结合律、分配律,没有交换律)。可以发现矩阵的加法和数乘和它完美匹配!因此矩阵可以作为一个向量空间。
于是,向量空间
当然有时我们并不需要那么多空间,好比一个人住一个城市……先不提城市各项环节能否正常运作,如果只是用来溜达的,那也是太过巨大了,有些地方可能你一辈子也取不到,还不如开始就不要。向量空间其实也可以像这样压缩范围,并且压缩后的向量空间也必须是全集
若向量空间
的子集 满足加法和数乘运算的封闭性,那么 是 的一个子空间。特殊地, 与 Undefined control sequence \bold 都是 的子空间, 称作零子空间,其他非零且不等于 Undefined control sequence \bold 的子空间称作真子空间(类比集合的空集、子集和真子集概念)。
在矩阵中,也存在零空间。它表现为矩阵方程
例 4.1.1 Merusea Village Portal 海露村传送门
自从你来到枫丹,知晓了水仙十字结社的秘密之后,奇怪的事情开始在你身边上演……
你在海露村遇见了抽象派美露莘大画师玛梅赫、以及一只发条机关狗西摩尔。很不巧,玛梅赫的作画颜料用完了,于是你们前去收集更加纯净的矿物颜料,期间玛梅赫邀请你们进入一个粉色的漩涡虫洞。或许是因为你前一天冒险到深夜,在这个温暖且舒适的环境下来了困意。一闭眼,再一睁眼,迎接你的不是如同往常一般的新地下区域 —— 而是一片温暖的、舒适的粉色幻境 —— 你被一个人丢在这个传送通道里了!
为了不让派蒙着急,同时也为了你能尽快在下一次困意席卷前逃出这个空间,你需要确定这个传送门是否为“同维度空间卷曲型”—— 即传送过程中不发生维度的变化。你需要证明你身处的空间是一个三维空间的子空间,这样才能使用正确的方法逃出生天。你发现你的身高和体宽的比值是原来的一半、但是体宽不变。请证明你所在的空间是是三维空间的子空间。
问题分析:首先要根据已有的信息判断该向量空间是否为三维向量空间的子集,然后再验证加法与数乘的封闭性,只有当二者均成立时才能够证明该空间是三维空间的子空间。
算法设计:根据题干最后一句话,我们不妨将主人公设为三维坐标系原点,按照
解:根据变换关系,得到该向量空间的集合形式
因此,所在空间
第二节 基底、张成与张集
假设
中有向量 Undefined control sequence \bold ,那么 称作向量 的线性组合。向量 的所有线性组合构成的集合叫向量 的张成。
我们都知道,

如果
- 若
- 向量平面
对于第一条,因为你怎么拟合平面,都不可能让你的平面比整个空间的维度更高,而且无论以什么系数搭配向量,它们所得的新向量都在整体空间内,第一条就能很简明的证明了。第二条性质,首先空间内向量的张成必为整个空间的子空间,毕竟用的都是数乘和加法,用的向量也都在空间内,总不能算一下加法向量就跑到空间外边去了吧,此外,因为数乘和加法的封闭性,任何经过这两个向量的空间都包含其张成,因此它是最小的。
l和张成相对,如果
张成 ,则 是 的张集。
基底,大家在高中立体几何部分学过了。当时的定义是:平面内不共线的两个向量叫做这个平面的一组基底。然而这段话可以用线性代数的语言原原本本描述出来:
在
维向量空间 中有 个线性无关的向量 ,则称它们是向量空间的一组基。
线性无关的概念,之前已经简单讲过,总的来说就是向量不共线,即不存在标量
例 4.2.1 Al-Ahmar’s Test 赤王的试炼
你和婕德一行人在圣显厅前击败了图谋不轨的镀金旅团,并在他们搭起的营帐里发现了一封密信。上面写着若想进入圣显厅,需先过三关试炼。为了能够一探黄金梦乡的秘密,你接下了完成三重试炼的任务,然而当你真正进入到第一重试炼时,却发现事情并没有这么简单……
你进入了试炼场地,却发现整个世界天旋地转。最终安定下来,你发现赤王的神奇科技把你带入了一个
维空间内。这还没完,四周又有整齐排列的空气墙阻挡了你的通路。经过好一顿摸索,你终于发现这是一个 维空间,于是你开始建立空间坐标系,五个坐标轴分别是 ,假设你现在所在的地方是原点 ,通关点 。四周的空气墙限制了你仅能沿着与向量 平行的方向行动。请问如何安排前进方向使得你能够从起点 到达终点 ?
问题分析:这个问题明显是让我们用
解:明显地,题中五个向量互相线性无关,因此可以作为该平面的一组基。由于向量加法和数乘运算的封闭性,且路径向量
设
因此,应在
因此一旦选定了平面的基底,该平面上所有的向量都可以用这组基底唯一表示出来,具体操作是使待求向量
基底可以表示平面内所有的向量,故
第三节 线性变换在高中数学中的应用
本节是 2024 年 12 月 29 日新加入的内容。是适合高中生体质的快速解题技巧。
一、基底法
在开始之前,我认为有必要再为读者回顾一下高二上册空间向量的相关内容。
有时,我们拿到的题目里不存在很明显的直角关系。设想这么一个平行六面体——它的底面是一个夹角为
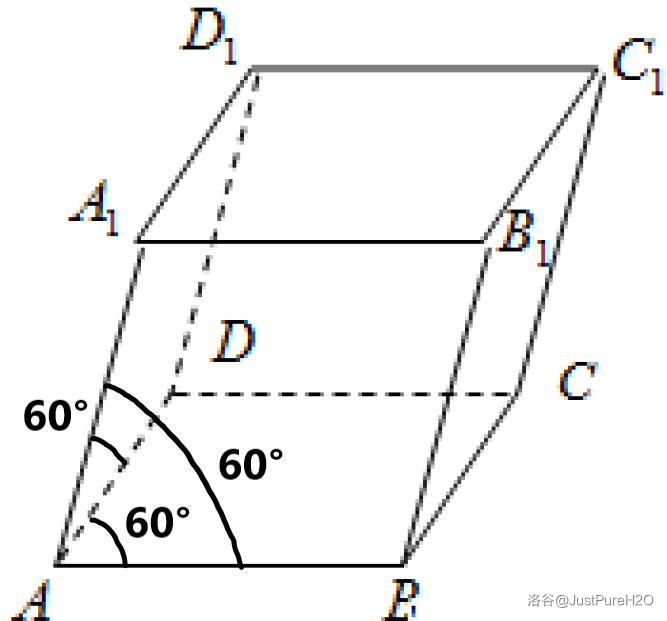
上图中,
一般来说将平行六面体的三条棱设置为基底会方便一些,因而空间中有基底向量
又或者,我们想要求出异面直线
像这样,根据角度关系巧妙设置基底、将一些向量用基底的线性组合表示,并进行计算的方法就叫做基底法。在存在特殊角度关系而难以建立空间直角坐标系的时候非常好用。
二、线性变换
我们先从平面直角坐标系入手,找到一般规律。假设我们有一组平面上的正交(垂直)单位基底
事实上,对于
第四节 线性基
本节主要是算法竞赛内容。
第二节里我们讲了向量空间的基底,基底其实还有一个名称叫线性基。平面中所有向量唯一对应一种基底的线性组合。在 OI 中常常被用于求第
一组值的异或和可以看做该空间内异或线性基的向量的异或组合,由于基底表示向量的唯一性:原集合中的数可以通过异或线性基里的基向量唯一确定。它有如下几个性质,事实上,它和普通平面内的实数线性基有相似之处:
- 原序列中任何元素都可以通过异或线性基内的元素异或得到
- 异或线性基不存在重复元素,且在保证性质一的前提下,它的元素最少
异或运算也有一个特殊性质,若
根据以上性质构造计算方法:
void insert(ll x){ for (int i = 63; i >= 0; i--) { if ((x >> i) & 1) { // 要存放的数的当前位为1 if (!p[i]) { p[i] = x; // 异或线性基该位为0,二进制下该位置为1 break; // 已找到位置存放,退出循环 } x ^= p[i]; // 异或线性基该位为1,为化为下三角形矩阵形式方便计算置为0 } }}由于一般题目中数据范围是 1e18,而转换为二进制位就有 unsigned long long,线性基 p 数组至少需要 60 位。
有时并不是所有的插入操作都会成功,因为要保证异或线性基里的向量互相线性无关。存储操作本质上是拆分二进制位,然后将它尽量表示为已有基向量的异或和,好像除去每个人身上的共同特征,只保留人的独特个性一般。如果拆到最后再也拆不了了,证明它是独特的,可以加入其中。反之,这个数就可以被其他数通过异或运算代替,没必要加它,返回插入失败。可以有下面的代码:
bool insert(ll x){ for (int i = 63; i >= 0; i--) { if ((x >> i) & 1) { if (!p[i]) { p[i] = x; // 异或线性基该位为0,二进制下该位置为1 break; // 已找到位置存放,退出循环 } x ^= p[i]; // 异或线性基该位为1,为化为下三角形矩阵形式方便计算置为0 } } return x; // 若被异或分解为0,则证明它可以被现有元素计算得到,为保证异或线性基元素互相线性无关,不予插入}如果是求一个数能否被这个异或线性基表示出来,将最后一行改为 return !x; 即可(能表示即不可插入,不能表示即可以插入)。若某次插入失败,证明 flag = false,在插入失败后设为 true 表示需要特判
线性基用于求解一组数的异或和最值问题,有下面求最值的三个例子。它们无一例外使用了贪心法:
一. 求最大值
ll xorMax(){ ll ans = 0; for (int i = 63; i >= 0; i--) { ans = max(ans, ans ^ p[i]); } return ans;}为什么从高位开始遍历?我们都知道如果一个数字的某位数大于另一个数字相同位置的数(两数数量级相同,即十进制下位数相同),那么前者是大于后者的。根据异或的运算法则:“不同为 ans 的高位此时是 0,若进行异或运算的同位数字是 0,即二者相同,结果为 0,不会变得更小;反之若异或运算的对应二进制位为 1,当前位异或结果是 1,变大了,因此 ans 高位为 1,运算数对应位为 0,结果为 1,不会变得更大;若运算数当前位是 1 异或结果为 0,变小了,所以
二. 求最小值
ll xorMin(){ ll ans = 0; if (flag) return 0; // 特判0 for (int i = 0; i <= 63; i++) { if (p[i]) return p[i]; }}我们知道,可以通过任意组合(异或运算)异或线性基中的元素来得出各种新的元素,若
三. 求第
这才是异或线性基的高级玩法
为了求第 rebuild。
void rebuild(){ for (int i = 63; i >= 0; i--) { // 从高位开始按位扫 for (int j = i - 1; j >= 0; j--) { // 遍历右移 if ((p[i] >> j) & 1) p[i] ^= p[j]; // 保证p[i]是异或线性基里第i位最小的那个,通过不断异或可以变小 } }}接着我们需要特判
ll queryKMax(ll k){ if (k == 1 && flag) return 0; // 特判 if (flag) k--; // 特判0,f(k)实为f(k-1) rebuild(); // 重构异或线性基 ll ans = 0; for (int i = 63; i >= 0; i--) { if (p[i]) { // 对k进行二进制分解 if (k & 1) ans ^= p[i]; // 位为1,异或 k >>= 1; } } return ans;}除了求值,异或线性基还可以合并,甚至于求它和另一个异或线性基的交集与并集。所以异或线性基是一种数据结构。我把它封装在一个结构体 XorBase 里:
struct XorBase { ll p[64]; bool flag;
XorBase() { flag = false; memset(p, 0, sizeof p); }
bool insert(ll n) { for (int i = 63; i >= 0; i--) { if ((n >> i) & 1) { if (!p[i]) { p[i] = n; break; } n ^= p[i]; } } if (!n) flag = true; return n; }
void rebuild() { for (int i = 63; i >= 0; i--) { for (int j = i - 1; j >= 0; j--) { if ((p[i] >> j) & 1) p[i] ^= p[j]; } } }
ll getMin() { if (flag) return 0; for (int i = 63; i >= 0; i--) { if (p[i]) return p[i]; } }
ll getMax() { ll ans = 0; for (int i = 63; i >= 0; i--) { ans = max(ans, ans ^ p[i]); } return ans; }
ll MaxK(ll k) { if (k == 1 && flag) return 0; if (flag) k--; rebuild(); ll ans = 0; for (int i = 63; i >= 0; i--) { if (p[i]) { if (k & 1) ans ^= p[i]; k >>= 1; } } return ans; }};四. 并集
思路就是枚举异或线性基
XorBase Union(XorBase A, XorBase B){ XorBase res = B; for (int i = 0; i <= 63; i++) { if (A.p[i]) { res.insert(A.p[i]); } } return res;}五. 交集
如果一个异或线性基里的元素插入到另一个异或线性基里会失败,则将它插入到交集异或线性基中。
XorBase Intersect(XorBase A, XorBase B){ XorBase res; for (int i = 0; i <= 63; i++) { if (A.p[i]) { if (!B.insert(A.p[i])) res.insert(A.p[i]); } if (B.p[i]) { if (!A.insert(B.p[i])) res.insert(B.p[i]); } } return res;}例 4.3.1 DMG Bonus 打核爆
作为一名资深神原玩家,你希望能在新限定五星角色初进卡池时尽快拿下全网首个 999w 核爆记录,以此证明自己的实力。现在你已经在游戏里做好了很多伤害加成型的食物,准备在 boss 战时一展身手。战斗开始时,你首先给角色吃下了基础食物(每局开始前必吃的食物),它的效果是在 300 秒内单角色爆发伤害增加
,但是同时它有一个副作用…… 基础食物生效期内,如果角色吃下其他伤害加成型的食物,总伤害加成的百分比数值将是各种食物的伤害百分比数值的异或之和,即
, 表示 , 为异或符号。各种食物的伤害加成在下边给出,如果不吃任何加成型食品(也不吃基础食品),爆发伤害期望值为 。吃完所有食物后,如果你用增伤角色施加了 的爆发增伤。请问你的最大爆发伤害能否达到 ,即 ?若不能,最高伤害是多少?(令每种食物只有一份,且食物效果均可叠加,结果四舍五入到万位)
| 编号 | 加成效果 |
|---|---|
| 1 | 270% |
| 2 | 200% |
| 3 | 280% |
| 4 | 200% |
| 5 | 180% |
| 6 | 150% |
| 7 | 75% |
问题分析:题干信息已经很明显了,这是一道异或线性基的最大和问题。根据上文所述程序计算即可。
算法实现:这里使用的是结构体封装版本的异或线性基计算代码:
#include <bits/stdc++.h>using namespace std;
typedef unsigned long long ll;
struct XorBase { ll p[64]; bool flag;
XorBase() { flag = false; memset(p, 0, sizeof p); }
bool insert(ll n) { for (int i = 63; i >= 0; i--) { if ((n >> i) & 1) { if (!p[i]) { p[i] = n; break; } n ^= p[i]; } } if (!n) flag = true; return n; }
void rebuild() { for (int i = 63; i >= 0; i--) { for (int j = i - 1; j >= 0; j--) { if ((p[i] >> j) & 1) p[i] ^= p[j]; } } }
ll getMin() { if (flag) return 0; for (int i = 63; i >= 0; i--) { if (p[i]) return p[i]; } }
ll getMax() { ll ans = 0; for (int i = 63; i >= 0; i--) { ans = max(ans, ans ^ p[i]); } return ans; }
ll MaxK(ll k) { if (k == 1 && flag) return 0; if (flag) k--; rebuild(); ll ans = 0; for (int i = 63; i >= 0; i--) { if (p[i]) { if (k & 1) ans ^= p[i]; k >>= 1; } } return ans; }} A;
int main(){ ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int n; cin >> n; for (int i = 1; i <= n; i++) { int x; cin >> x; A.insert(x); } cout << (1400000 * (A.getMax() + 60 + 70) / 100) << endl; return 0;}运行代码,在输入框输入:
727020028020018015075结果输出:8162000.000。小于所给的 816 万。
洛谷例题:
后记 & 鸣谢
本文的灵感来源正是例 1.4.1,感谢这样的高智商解谜让我沉迷于线性代数无法自拔。
本文的结构安排和部分证明过程均借鉴了
感谢 @Brailliant11001 为本文例 2.2.1 进行答案检验;@HYLW 为本文 1.3 节消元步骤进行查验;向量空间部分图片取自知乎,其余图片资源引用时请注明出处;章节例题/代码均为原创,如有错漏之处可私信我指出。
支持与分享
如果这篇文章对你有帮助,欢迎分享给更多人或赞助支持!
部分内容可能已过时

































































































